情報幾何の基礎輪読会 #1
- 2. 2 本?日の内容本?日の内容 第第 00 章章:: 準备準备 第第 11 章章: Euclid: Euclid 平?面の幾何平?面の幾何
- 3. 3 第第 00 章章 準备準备
- 4. 4 . 1 0.10.1 微積より微積より ~~逆写像定理逆写像定理//陰関数定理陰関数定理~~
- 5. 4 . 2 微分可能性微分可能性??JacobiJacobi?行列?行列 f : D(?R ) →Rl n がが x = ax = a で微分可能で微分可能 s.t. f(a + h) = f(a) + Ah + o(∥h∥) このときのこのときの AA はは ff のの JacobiJacobi ?行列?行列 i.e. A = ( )?xk ?fj (j,k) ? ?A ∈ M(n, l)
- 6. 4 . 3 記号の導?入記号の導?入 F(x, y) : D(?R ×R ) →R : C mapk n n r F(a, b) = c 以下以下 R := a ×R0 n { } n R :=R × b0 k k { } :: 縦軸縦軸 :: 横軸横軸
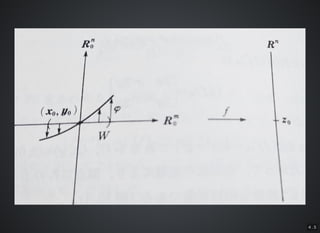
- 7. 4 . 4 陰関数定理陰関数定理 FF のの ''縦軸縦軸'' への制限のヤコビ?行列への制限のヤコビ?行列 (a, b)?y ?F が正則の時、が正則の時、''横軸横軸'' におけるにおける aa の開近傍の開近傍 WW とと φ : W →R : Cn r が存在して次のが存在して次の 1, 21, 2 が成?立が成?立 1. F(x, φ(x)) = c (?x ∈ W) 2. (a) = ??x ?φ ?y ?F ?1 ?x ?F
- 8. 4 . 5
- 10. 4 . 7 逆写像定理逆写像定理 f : D(?R ) →R : C mapn n r 1. ?x ?f がが x = ax = a で正則で正則 2. a2. a の開近傍の開近傍 UU が存在してが存在して f∣ : U ? f(U) : C diffeoU r に対し、に対し、1,21,2 は同値は同値
- 11. 4 . 8 22→→11)) g ° f = idU逆写像逆写像 g(y)g(y) をもって来るとをもって来ると = I?y ?g ?x ?f 微分して微分して よりより □□
- 12. 4 . 9 11→→2)2) F :R × D →Rn n F(x, y) = x ? f(y) とするととすると = ??y ?F ?y ?f はは (f(a), a )(f(a), a ) の周りで正則の周りで正則 陰関数定理より陰関数定理より f(a)f(a) の開近傍の開近傍 WW の周りでの周りで ?g : W → D s.t. F(x, g(x)) = F(f(a), a) = 0 ? x = f(g(x)) □□
- 13. 4 . 10 例:例: f :R ? x ? Ax ∈RA n n が逆写像を持つが逆写像を持つ ?? AA が正則が正則 逆写像定理が逆写像定理が globalglobal で成り?立つ場合で成り?立つ場合
- 14. 4 . 11 逆写像定理逆写像定理→→陰関数定理陰関数定理 ∵) F : D(?R ×R ) → Rk n n が陰関数定理の仮定を満たすとする。が陰関数定理の仮定を満たすとする。 f : D →R ×Rk n を次で定める。を次で定める。 f(x, y) := (x, F(x, y))
- 15. 4 . 12 ff のの JacobiJacobi ?行列?行列 Jf = ( I ?x ?F 0 ?y ?F ) は仮定から正則は仮定から正則→→逆写像定理が成?立逆写像定理が成?立 f (x, y) = (x, g(x, y))?1 となる、となる、 gg をもちいて、をもちいて、 g(?, b) が題意を満たすが題意を満たす □□
- 16. 5 . 1 0.20.2 線形代数より線形代数より ~~双対とテンソル双対とテンソル~~
- 17. 5 . 2 双対空間双対空間 V : R 上の上の''有限次元有限次元'' ベクトル空間、に対しベクトル空間、に対し V := f : V → R ∣ linear? { } を、を、VV の双対空間というの双対空間という 1. dim(V ) = dim(V )? 2. (V ) ? V? ? Prop)Prop)
- 18. 5 . 3 ∵∵)) 1) V1) V の基底の基底 e{ i}i=1,...n その双対基底その双対基底 f{ j }j=1,...n を取れば、を取れば、 おkおk 実際、実際、 ?f ∈ V , a := f(e )? i i と置くと、と置くと、 f = a fj j (∵ e{ i} が基底が基底 を?一つとるを?一つとる
- 19. 5 . 4 2 )2 ) x ? x~ w/ : f ? f(x)x~ とすると、これは明らかに単射とすると、これは明らかに単射 dimV = dmV = dim(V )? ? ? かつかつ より同型より同型 □□
- 20. 5 . 5 V := F ∈ ((V ) × V ) ∣ multi linear(r,s) { ? r s ? } をを rr 階反変階反変, s, s 階共変テンソル空間という階共変テンソル空間という V = V ? ... ? V ? V ? ... ? V(r,s) ? ? r 個 s 個 と書くことが普通な気がすると書くことが普通な気がする...(...(※※)) 特に特に V = ?V(r,0) : r: r 階反変テンソル空間階反変テンソル空間 V = ?V(0,s) ? : s: s 階共変テンソル空間階共変テンソル空間 dimV = (dimV )(r,s) r+s
- 21. 5 . 6 補?足:テンソル積の性質補?足:テンソル積の性質 V ? W ? W ? V (V ? W) ? U ? V ? (W ? U) V ? R ? R ? V ? V より、上のより、上の (r, s)(r, s) という書き?方はという書き?方はwell-de?nedwell-de?ned
- 22. 5 . 7 ※※についてについて Φ : V × (V ) → Vr ? s (r,s) Φ(v , ..., v , f , ..., f ) =1 r 1 s (g , ..., g , w , ..., w ) ? g (v ) ? f (w )1 r 1 s ∏ i i ∏ j j をを と定めると定める
- 23. 5 . 8 e : V{ i} の基底としの基底とし f : V{ j } ? の双対基底として、の双対基底として、 Φ(e , ..., e , f , ..., f ){ i1 ir j1 js } がが V (r,s) の基底になることから従うの基底になることから従う
- 24. 6 . 1 1. Euclid1. Euclid 平?面の幾何平?面の幾何
- 26. 7 . 1 1.11.1 座标系座标系
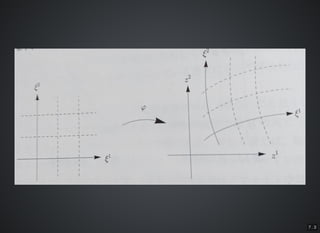
- 27. 7 . 2 φ :R →R , (ξ , ξ ) ? (z , z )2 2 1 2 1 2 は逆写像定理より、は逆写像定理より、 JacobiJacobi?行列?行列 Jφ = ( )?ξa ?zi i,a∈ 1,2{ } が正則であれば、が正則であれば、locallocal には微分同相には微分同相 従って特に、従って特に、 座標軸の像は?行き先での座標軸の像は?行き先での ""座標軸座標軸"" と考えられると考えられる→→「曲線座標系」!!「曲線座標系」!!
- 28. 7 . 3 え
- 29. 7 . 4 例1例1??斜交座標系斜交座標系 φ(x) := Ax + b for A ∈ GL(2, R), b ∈R2 により定まる座標系:アフィン座標系により定まる座標系:アフィン座標系
- 30. 7 . 5 例2:極座標系例2:極座標系 φ : (r, θ) ? (z , z )1 2 をを =[ z1 z2 ] [ rcosθ rsinθ ] で、与えるで、与える((ご存知極座標ご存知極座標)) det(Jφ) = det = r[ cosθ sinθ ?rsinθ rcosθ ] より、より、 r ≠ 0r ≠ 0 で曲線座標を与える。で曲線座標を与える。
- 31. 8 . 1 1.21.2 接ベクトル接ベクトル
- 32. 8 . 2 φ = (x , x ) ? (z , z ) : U(?R ) → M1 2 1 2 2 座標曲線座標曲線: given: given C (t) = φ(t, 0)p とし、点とし、点 P = φ(0, 0) でのでの xx11 ?方向への接ベクトルを次で与える?方向への接ベクトルを次で与える:: e (P) := (0)x1 dt dCp xx22 ?方向も同様?方向も同様 □□
- 33. 8 . 3 ?一般の?方向の接ベクトルを考える?一般の?方向の接ベクトルを考える i.e. T (M) = (0) ∣ c(0) = PP {dt dc } Lem : ?e , e ? = T (M)x1 x2 P ??十分?小さくすると、??十分?小さくすると、∵) ε > 0 : c(?ε, ε) ? U : 座標近傍とできる座標近傍とできる c(t) = φ(? (t)), t ∈ (?ε, ε)c~ = + = v edt dc ?x1 ?φ dt dx1 ?x2 ?φ dt dx2 i xi □□
- 34. 8 . 4 座標変換すると座標変換すると...... v ei xi = vi ?xi ?φ = vi ?xi ?(ψ°ψ °φ)?1 = vi ?ξa ?ψ ?xi ?ξa = (v )ei ?xi ?ξa ξa = v ea ξa v = va ?xi ?ξa i すなわち、すなわち、 座標変換関数の座標変換関数の JacobiJacobi ?行列で調節される。?行列で調節される。
- 36. 9 . 2 wikiwiki にいい?言葉があったにいい?言葉があった “ Na?vely, one may consider a vector ?eld parallelNa?vely, one may consider a vector ?eld parallel if the coordinate components of the vector ?eld areif the coordinate components of the vector ?eld are constant along the curve. However, an immediateconstant along the curve. However, an immediate ambiguity arises: in which coordinate systemambiguity arises: in which coordinate system should these components be constant?should these components be constant? 平?行ベクトル場平?行ベクトル場
- 37. 9 . 3 ちょっとだけ?一般論ちょっとだけ?一般論((曲?面論的な曲?面論的な)) 空間内の曲?面空間内の曲?面 MM および、曲線および、曲線 cc を考えるを考える MM 内の内の cc に沿ったベクトル場とは:に沿ったベクトル場とは: t ? X ∈ T Mt c(t) XX の微分を接?方向と法線?方向に分けて、の微分を接?方向と法線?方向に分けて、 以下のように書くこととする。以下のように書くこととする。 = + Adt dXt dt DXt X
- 38. 9 . 4 定義定義)) 曲線曲線 cc に沿ったベクトル場が平?行に沿ったベクトル場が平?行 ?? 微分の接?方向の成分が消える微分の接?方向の成分が消える 定義定義)) 曲線曲線 cc が測地線が測地線 ?? cc の微分がの微分が cc ?自?身に沿って平?行?自?身に沿って平?行
- 39. 9 . 5 例例))ユークリッド空間の測地線は等速直線運動ユークリッド空間の測地線は等速直線運動 ∵∵) c) c が測地線が測地線 ? = 0dt2 d c2 より明らかより明らか □□
- 41. 10 . 1 テキスト、ちょっと迷?走気味なので。。。テキスト、ちょっと迷?走気味なので。。。 X∣ : t ? Xc c(t) ベクトル場ベクトル場 XX および曲線および曲線 cc に対してに対して により、曲線に沿ったベクトル場が定まるにより、曲線に沿ったベクトル場が定まる ベクトルベクトル vv に対して、に対して、 vv の積分曲線の積分曲線 ccvv
- 42. 10 . 2 = X∣ + Adt dX∣cv dt D cv X∣cv のように接?方向と法線?方向に分解するのように接?方向と法線?方向に分解する ? Xv この時の第この時の第 11 項を項を と書き共変微分というと書き共変微分という
- 43. 10 . 3 ChristoffelChristoffel シンボルシンボル e{ xj }座標系からさだまる基本基底座標系からさだまる基本基底 に対して、共変微分をした時の係数がに対して、共変微分をした時の係数が Christoffel SymbolChristoffel Symbol i.e. ? e = Γ eexj xi ji k xk により、により、Christoffel SymbolChristoffel Symbol を定めるを定める
- 44. 10 . 4 例:極座標の共変微分例:極座標の共変微分 e = (cosθ, sinθ), e = (?rsinθ, rcosθ)r θ と定義から、(※) ? e = 0r r ? e = (?sinθ, cosθ) = er θ r 1 θ ? e = (?rcosθ, ?rsinθ) = ?reθ θ r ? e = (?sinθ, cosθ) = eθ r r 1 θ
- 45. 10 . 5 の積分曲線は極座標で書くとの積分曲線は極座標で書くとer c (t) = (r + t, θ)r e ∣ = (?(r + t)sinθ, (r + t)cosθ)θ c (t)r と例えば取ると例えば取る 時間で微分して、時間で微分して、 ? e = (?sinθ, cosθ) = er θ r 1 θ を得る。以下同様を得る。以下同様 □□ ※※の補?足の補?足
- 46. 11 終わり終わり




















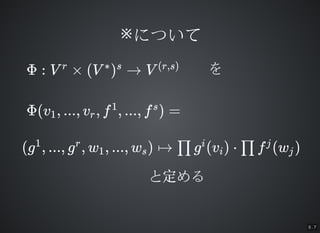






![7 . 5
例2:極座標系例2:極座標系
φ : (r, θ) ? (z , z )1 2 をを
=[
z1
z2
] [
rcosθ
rsinθ
]
で、与えるで、与える((ご存知極座標ご存知極座標))
det(Jφ) = det = r[
cosθ
sinθ
?rsinθ
rcosθ
]
より、より、 r ≠ 0r ≠ 0 で曲線座標を与える。で曲線座標を与える。](https://image.slidesharecdn.com/infogeo1-160123054947/85/1-30-320.jpg)















