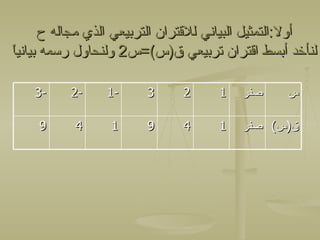
Ў™ўЕЎЂўКўД ЎІўДЎ£ўВЎ™Ў±ЎІўЖЎІЎ™ ЎІўДЎ™Ў±Ў®ўКЎєўКЎ© 1
- 2. вАЂЎ™ўЕЎЂўКўД ЎІўДўВЎ™Ў±ЎІўЖЎІЎ™ ЎІўДЎ™Ў±Ў®ўКЎєўКЎ©вАђ вАЂўКўЕўГўЖўЖЎІ ЎІЎ≥Ў™ЎЃЎѓЎІўЕ ЎІўДЎ±Ў≥ўЕ ЎІўДЎ®ўКЎІўЖўК ўДЎ≠ўД ЎІўДўВЎ™Ў±ЎІўЖвАђ вАЂЎІўДЎ™Ў±Ў®ўКЎєўК ўВ)Ў≥(=Ў£Ў≥2+Ў® Ў≥+Ўђ, ўГўЕЎІ Ў≥ўКЎ™ЎґЎ≠вАђ вАЂўЕўЖ ЎІўДўЕЎЂўДЎ© ЎІўДўДЎ≠ўВЎ© , ўИўДўГўЖ ЎѓЎєўЖЎІ Ў£ўИ ўЛ ўЖЎ™ЎєЎ±ўБвАђ вАЂўДвАђ вАЂЎЈЎ±ўКўВЎ© Ў±Ў≥ўЕ ЎІўДўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±Ў®ўКЎєўК .вАђ
- 3. вАЂЎІўДўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±Ў®ўКЎєўК ўЗўИ ўГўД ЎІўВЎ™Ў±ЎІўЖ )Ў≥( ўКўЕўГўЖвАђ вАЂўГЎ™ЎІЎ®Ў™ўЗ ЎєўДўЙ ЎІўДЎµўИЎ±Ў©:ўВ)Ў≥(=Ў£Ў≥2+Ў® Ў≥+ЎђвАђ вАЂЎ≠ўКЎЂ Ў£ Ў® Ўђ Ў™ўЖЎ™ўЕўК Ў≠ ,Ў£ ўД Ў™Ў≥ЎІўИўК ЎµўБЎ±.вАђ
- 4. вАЂўДўКўГўЖ ўВ)Ў≥(=Ў≥ +5Ў≥-6 Ў£ўИЎђЎѓ:вАђ вАЂ2вАђ вАЂўВ)0(,ўВ)-1(,ўВ)1(,ўВ)2(,ўВ)-3(.вАђ вАЂўВ)0(=ЎµўБЎ±2+5√ЧЎµўБЎ±-6=-6.вАђ вАЂўВ)-1(=)-1(2+5√Ч-1_6=1_5=-01.вАђ вАЂўВ)1(=)1(2+5√Ч1-6=1+5_6=ЎµўБЎ±.вАђ вАЂўВ)2(=)2(2+5√Ч-6=4+01_6=8.вАђ вАЂўВ)-3(=)-3(2+5√Ч-3-6=9+-51-6=-21вАђ
- 5. вАЂЎ•Ў∞ЎІ ўГЎІўЖ ўВ)Ў≥(=3-Ў≥2,Ў£ўИЎђЎѓ:вАђ вАЂўВ)1(,ўВ)-1(,ўВ)2(,ўВ)0(,ўВ)-2(,ўВ)Ў£+1(.вАђ вАЂўВ)1(=3_)1(2=2,ўВ)-1(=3_)-1(2=2вАђ вАЂвА™пБЃвАђвАђ вАЂўВ)2(=3_)-2(2=_1,ўВ)0(=3_)0(2=3вАђ вАЂўВ)-2(=3_)-2(2=-1,ўВ)Ў£+1(=3_)Ў£+1(2вАђ
- 6. вАЂЎ•Ў∞ЎІ ўДўЕ ўПЎ≠ЎѓЎѓ ЎІўДўЕЎђЎІўД ўБўК ЎІўДЎ≥Ў§ЎІўД ўКЎєЎ™Ў®Ў± ЎІўДўЕЎђЎІўДвАђ вАЂўКвАђ вАЂЎђўЕўКЎє ЎІўДЎєЎѓЎІЎѓ ЎІўДЎ≠ўВўКўВўКЎ© Ў≠ Ў£ўЕЎІ ўЕЎѓўЙ ЎІўДўВЎ™Ў±ЎІўЖвАђ вАЂўБўЗўИ ўЕЎђўЕўИЎєЎ© ЎђўЕўКЎє ЎІўДўВўКўЕ ЎІўДўЕўЕўГўЖЎ© ўДўДўВЎ™Ў±ЎІўЖ.вАђ
- 7. вАЂЎ£ўИўД:ЎІўДЎ™ўЕЎЂўКўД ЎІўДЎ®ўКЎІўЖўК ўДўДўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±Ў®ўКЎєўК ЎІўДЎ∞ўК ўЕЎђЎІўДўЗ Ў≠вАђ вАЂЎІвАђ вАЂўДўЖЎ£ЎЃЎѓ Ў£Ў®Ў≥ЎЈ ЎІўВЎ™Ў±ЎІўЖ Ў™Ў±Ў®ўКЎєўК ўВ)Ў≥(=Ў≥2 ўИўДўЖЎ≠ЎІўИўД Ў±Ў≥ўЕўЗ Ў®ўКЎІўЖўКўЛвАђ вАЂ-3вАђ вАЂ-2вАђ вАЂ-1вАђ вАЂ3вАђ вАЂ2вАђ вАЂ1вАђ вАЂЎµўБЎ±вАђ вАЂЎ≥вАђ вАЂ9вАђ вАЂ4вАђ вАЂ1вАђ вАЂ9вАђ вАЂ4вАђ вАЂ1вАђ вАЂўВ)Ў≥( ЎµўБЎ±вАђ
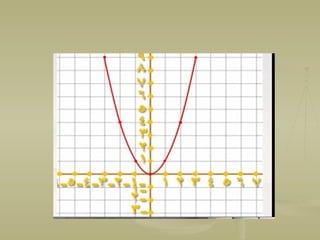
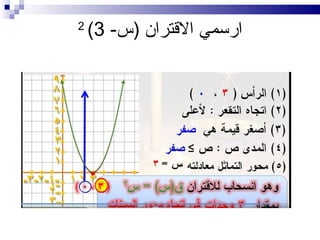
- 9. вАЂўИЎ•Ў∞ЎІ Ў≠ЎІўИўДўЖЎІ ЎѓЎ±ЎІЎ≥Ў© ўЗЎ∞ЎІ ЎІўДўВЎ™Ў±ЎІўЖ Ў®ЎіўГўД Ў£ўГЎЂЎ± ўБЎ•ўЖўЖЎІ ўЖўДЎ≠ЎЄ ўЕЎІ Ў®Ў£Ў™ўК:вАђ вАЂ1(Ў£ЎµЎЇЎ± ўВўКўЕЎ© ўКЎ£ЎЃЎ∞ўЗЎІ ЎІўДўВЎ™Ў±ЎІўЖ ўЗўК ЎµўБЎ± ўИЎ™Ў≠ЎѓЎЂ ЎєўЖЎѓ ЎІўДўЖўВЎЈЎ©вАђ вАЂ)0,0(вАђ вАЂ2(ЎІўДўВЎ™Ў±ЎІўЖ ўЕЎ™ўЕЎІЎЂўД Ў≠ўИўД ўЕЎ≠ўИЎ± ЎІўДЎµЎІЎѓЎІЎ™.вАђ вАЂ3(ўЕЎѓўЙ ЎІўДўВЎ™Ў±ЎІўЖ {Ўµ:Ўµ вЙ§ ЎµўБЎ±}вАђ вАЂ4(ЎІўДўЖўВЎЈЎ©)0,0(Ў™Ў≥ўЕўЙ ЎІўДЎ±Ў£Ў≥.вАђ вАЂ5(ўКЎ≥ўЕўЙ ЎІўДўЕўЖЎ≠ўЖўЙ ЎІўДўЕЎ±Ў≥ўИўЕ Ў£ЎєўДўЗ ўВЎЈЎє ўЛ ўЕўГЎІўБЎ¶ ўЛ.вАђ вАЂЎІвАђ вАЂЎІвАђ
- 10. вАЂЎ•ўЖ ЎІўДЎ™ўЕЎЂўКўД ЎІўДЎ®ўКЎІўЖўК ўДўК ЎІўВЎ™Ў±ЎІўЖ Ў™Ў±Ў®ўКЎєўК ўЗўИ ўВЎЈЎєвАђ вАЂўЕўГЎІўБўЙЎ°.вАђ
- 11. вАЂЎІўДўВЎ™Ў±ЎІўЖ ўВ)Ў≥(=Ў≥2+ўЖ ўЗўИ ЎІўЖЎ≥Ў≠ЎІЎ® ўДўДўВЎ™Ў±ЎІўЖвАђ вАЂўВ)Ў≥(=Ў≥ Ў®ўЕўВЎѓЎІЎ±ўЖвАђ вАЂ2вАђ вАЂўИЎ≠ЎѓЎ© Ў®ЎІЎ™ЎђЎІўЗ ўЕЎ≠ўИЎ± ЎІўДЎµЎІЎѓЎІЎ™ ЎІўДўЕўИЎђЎ® Ў•Ў∞ЎІ ўГЎІўЖЎ™вАђ вАЂўЖ ўЕўИЎђЎ®Ў© ўИЎІўДЎ≥ЎІўДЎ® Ў•Ў∞ЎІ ўГЎІўЖЎ™ ўЖ Ў≥ЎІўДЎ®Ў© .вАђ
- 12. вАЂ3вАђ вАЂ2+вАђ вАЂЎІЎ±Ў≥ўЕўК ЎІўДўВЎ™Ў±ЎІўЖ Ў≥вАђ
- 13. вАЂЎІўДўВЎ™Ў±ЎІўЖ ўВ)Ў≥(=)Ў≥_ўЕ(2 ўЗўИ ЎІўЖЎ≥Ў≠ЎІЎ®вАђ вАЂўДўДўВЎ™Ў±ЎІўЖ ўВ)Ў≥(=Ў≥2 Ў®ўЕўВЎѓЎІЎ± ўЕ Ў®ЎІЎ™ЎђЎІўЗвАђ вАЂўЕЎ≠ўИЎ± ЎІўДЎ≥ўКўЖЎІЎ™ ЎІўДўЕўИЎђЎ® Ў•Ў∞ЎІ ўГЎІўЖЎ™ ўЕ ўЕўИЎђЎ®Ў©вАђ вАЂўИЎІўДЎ≥ЎІўДЎ® Ў•Ў∞ЎІ ўГЎІўЖЎ™ ўЕ ЎІўДЎ≥ЎІўДЎ®Ў©.вАђ
- 14. вАЂ2вАђ вАЂЎІЎ±Ў≥ўЕўК ЎІўДўВЎ™Ў±ЎІўЖ )Ў≥- 3(вАђ
- 15. вАЂЎ•ўЖ ЎІўДЎ™ўЕЎЂўКўД ўДўДўВЎ™Ў±ЎІўЖ ўВ)Ў≥(=)Ў≥-ўЕ(2 +ўЖ ўЗўИвАђ вАЂЎІўЖЎ≥Ў≠ЎІЎ® ўДўДўВЎ™Ў±ЎІўЖ ўВ)Ў≥(=Ў≥2 Ў®ўЕўВЎѓЎІЎ± ўЕ ўИЎ≠ЎѓўЗвАђ вАЂЎ®Ў•Ў™ЎђЎІўЗ ўЕЎ≠ўИЎ± ЎІўДЎ≥ўКўЖЎІЎ™ ЎЂўЕ ўЖ ўИЎ≠ЎѓЎ© Ў®Ў•Ў™ЎђЎІўЗ ўЕЎ≠ўИЎ±вАђ вАЂЎІўДЎµЎІЎѓЎІЎ™ ўИЎ™ўГўИўЖ ЎІЎ≠ЎѓЎІЎЂўКЎІЎ™ Ў±Ў£Ў≥ ЎІўДўВЎЈЎєвАђ вАЂЎІўДўЕўГЎІўБўЙЎ° ўЗўК )ўЕ,ўЖ(.вАђ
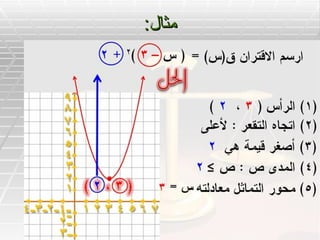
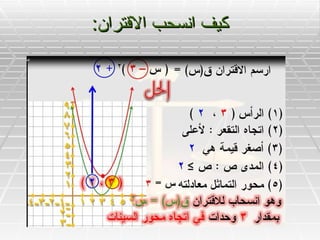
- 17. вАЂўЕЎЂЎІўД:вАђ
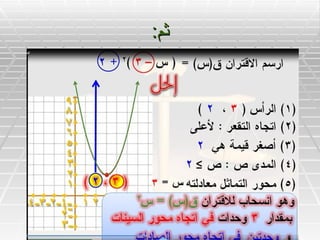
- 19. вАЂЎЂўЕ:вАђ
- 20. вАЂЎЂЎІўЖўКўЛ: ЎІЎ≥Ў™ЎЃЎѓЎІўЕ ЎІўДЎ™ўЕЎЂўКўД ЎІўДЎ®ўКЎІўЖўК ўБўК Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ©вАђ вАЂЎІвАђ вАЂЎІўДЎ™Ў±Ў®ўКЎєўКўЗ.вАђ
- 21. вАЂЎІЎ±Ў≥ўЕ ЎІўДўЕўЖЎ≠ўЖўЙ ЎІўДЎ™ўВЎ±ўКЎ®ўК ўДўДўВЎ™Ў±ЎІўЖвАђ вАЂўВ)Ў≥(=Ў≥2-4Ў≥+1 ЎЂўЕ ЎІЎ≥Ў™ЎЃЎѓўЕ ЎІўДЎ±Ў≥ўЕ ўБўК Ў≠ўДвАђ вАЂЎІўДўЕЎєЎІЎѓўДЎ© Ў≥2-4Ў≥+1=ЎµўБЎ±вАђ вАЂЎІўДЎ≠ўД:ўЖЎ≠ЎІўИўД ЎІўДўГЎ™ЎІЎ®ўЗ Ў≥2-4Ў≥+1ЎєўДўЙ ЎµўИЎ±Ў© )Ў≥_ўЕ(2 +ўЖвАђ вАЂЎ≥2_4Ў≥+1 =)Ў≥2-4Ў≥+4(+1-4вАђ вАЂ=)Ў≥-2(2+-3вАђ вАЂ=)Ў≥-2(2+-3вАђ вАЂЎІўДЎ±Ў£Ў≥ )2ўИ-3( Ў•ўЖ Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© Ў≥2-4Ў≥+1=ЎµўБЎ± ўЗўИвАђ вАЂЎІўДЎ≠ЎѓЎІЎЂўК ЎІўДЎ≥ўКўЖўК ўДўЖўВЎЈЎ© Ў™ўВЎІЎЈЎє ЎІўДўВЎ™Ў±ЎІўЖ Ў≥2-4Ў≥+1ўЕЎєвАђ вАЂўЕЎ≠ўИЎ± ЎІўДЎ≥ўКўЖЎІЎ™ ўИўЕўЖ ЎІўДЎ±Ў≥ўЕ ўЖўДЎ≠ЎЄ Ў£ўЖ Ў≥=ўЂ3 0ЎЫЎ≥=ўЂ7 3вАђ