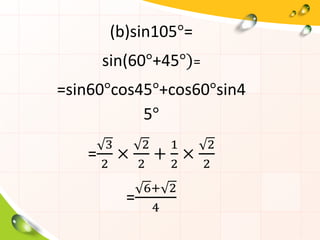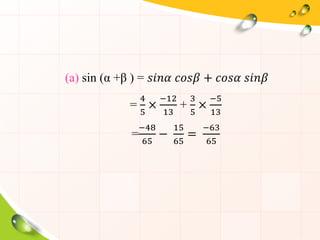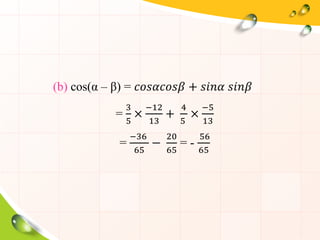ўЕЎ™ЎЈЎІЎ®ўВЎІЎ™ ЎІўДўЕЎђўЕўИЎє ўИЎІўДўБЎ±ўВ
- 1. L/O/G/O вАЂўВвАђвАЂўИЎІўДўБЎ±вАђ вАЂЎІўЕўДЎђўЕўИЎєвАђ вАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ um and difference identities вАЂЎІўДЎЂЎІўЖўИўКЎ©вАђ вАЂўВЎ±ЎЈЎ®Ў©вАђ вАЂЎ≥Ў©вАђвАЂЎ±вАђвАЂўЕЎѓвАђ/вАЂЎ®ўЖЎІЎ™вАђ вАЂЎІўДЎ±ўКЎІЎґўКЎІЎ™вАђ вАЂўВЎ≥ўЕвАђ вАЂЎєўДўЕўКвАђ вАЂЎєЎіЎ±вАђвАЂЎІўДЎ≠ЎІЎѓўКвАђ вАЂўДўДЎµўБвАђ вАЂЎєўЕўДвАђвАЂЎіЎ©вАђвАЂЎ±вАђвАЂўИвАђ вАЂЎІўДЎЂЎІўЖўКвАђ вАЂўКвАђ вАЂЎІЎ≥вАђвАЂЎ±вАђвАЂЎІўДЎѓвАђвАЂЎІўДўБЎµўДвАђ вАЂЎ®ўЖЎѓвАђ(9вАУ4) вАЂЎІўДўВЎ≥ўЕвАђ вАЂЎ¶ўКЎ≥Ў©вАђвАЂЎ±вАђ/вАЂЎ£вАђ.вАЂЎІўДЎєЎѓЎІўИўЖўКвАђвАЂўЕўЖўКЎ±Ў©вАђ вАЂЎ≥Ў©вАђвАЂЎ±вАђвАЂЎІўЕўДЎѓвАђвАЂўЕЎѓўКЎ±Ў©вАђ/вАЂЎ£вАђ.вАЂЎІўЕўДўКЎ±вАђ вАЂЎЃЎІўДЎѓЎ©вАђ вАЂЎІўДўБўЖўКвАђ вАЂЎІўЕўДўИЎђўЗвАђ/вАЂЎ£вАђ.вАЂЎІўДЎѓўКўЖвАђ вАЂЎ±вАђвАЂўЖўИвАђ вАЂЎєЎ®ЎѓЎІўДўИўЗЎІЎ®вАђ вАЂЎІЎ£ўДўИўДўЙвАђ вАЂЎІўЕўДўИЎђўЗЎ©вАђ/вАЂЎ£вАђ.вАЂЎІўДЎєўДўКвАђ вАЂЎ≠ЎµЎ©вАђ
- 2. вАЂЎІўДЎ≥ўДўИўГўКЎ©вАђ вАЂЎІЎ£ўДўЗЎѓЎІўБвАђ.. вАЂЎ£ўЖвАђ вАЂЎєўДўКвАђвАЂўВЎІЎѓЎ±вАђвАЂЎІўДЎЈЎІўДЎ®вАђ вАЂўЖвАђвАЂўКўГўИвАђ вАЂЎ£ўЖвАђ вАЂўКЎ™ўИўВЎєвАђвАЂЎІўДЎ®ўЖЎѓвАђвАЂўЖўЗЎІўКЎ©вАђ вАЂўБўКвАђ: 1)вАЂЎІўЕўДЎ™ўГЎІўБЎ¶Ў©вАђвАЂЎІўДЎѓўИЎІўДвАђвАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂўКЎ∞ўГЎ±вАђ. 2)вАЂЎІўЕўДЎ™ўГЎІўБЎ¶Ў©вАђвАЂЎІўДЎѓўИЎІўДвАђвАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂЎ®ЎІЎ≥Ў™ЎЃЎѓЎІўЕвАђвАЂЎІўЕўДЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂЎ®ЎєЎґвАђвАЂЎµЎ≠Ў©вАђ вАЂўКЎЂЎ®Ў™вАђ. 3)вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂўЕўДЎђўЕўИЎєвАђвАЂЎІўДЎ™ўЕЎІўЕвАђ вАЂЎђўКЎ®вАђвАЂўЖвАђвАЂўВЎІўЖўИвАђ вАЂўКЎ≥Ў™ўЖЎ™ЎђвАђ. 4)вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂЎ®ўКўЖвАђ вАЂўВвАђвАЂўДўДўБЎ±вАђвАЂЎІўДЎ™ўЕЎІўЕвАђ вАЂЎђўКЎ®вАђ вАЂўЖвАђвАЂўВЎІўЖўИвАђ вАЂўКЎ≥Ў™ўЖЎ™ЎђвАђ. 5)вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂўЕўДЎђўЕўИЎєвАђ вАЂЎІўДЎђўКЎ®вАђвАЂўЖвАђвАЂўВЎІўЖўИвАђ вАЂўКЎ≥Ў™ўЖЎ™ЎђвАђ. 6)вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂЎ®ўКўЖвАђ вАЂўВвАђвАЂўДўДўБЎ±вАђ вАЂЎІўДЎђўКЎ®вАђвАЂўЖвАђвАЂўВЎІўЖўИвАђ вАЂўКЎ≥Ў™ўЖЎ™ЎђвАђ.
- 3. 7)вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂўЕўДЎђўЕўИЎєвАђ вАЂЎІўДЎЄўДвАђвАЂўЖвАђвАЂўВЎІўЖўИвАђ вАЂўКЎ≥Ў™ўЖЎ™ЎђвАђ. 8)вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂЎ®ўКўЖвАђ вАЂўВвАђвАЂўДўДўБЎ±вАђ вАЂЎІўДЎЄўДвАђвАЂўЖвАђвАЂўВЎІўЖўИвАђ вАЂўКЎ≥Ў™ўЖЎ™ЎђвАђ. 9)вАЂЎІўДЎЃЎІЎµЎ©вАђвАЂЎІўКЎІвАђвАЂўИвАђвАЂўДўДЎ≤вАђвАЂЎІўЕўДЎЂўДЎЂўКЎ©вАђ вАЂЎІўДўЖЎ≥Ў®вАђ вАЂўКЎ∞ўГЎ±вАђ. 10)вАЂЎІўКЎІвАђвАЂўИвАђвАЂЎІўДЎ≤вАђвАЂўДЎ®ЎєЎґвАђвАЂЎІўЕўДЎЂўДЎЂўКЎ©вАђ вАЂЎІўДўЖЎ≥Ў®вАђвАЂЎІЎҐўДўДЎ©вАђ вАЂЎІЎ≥Ў™ЎЃЎѓЎІўЕвАђ вАЂўЖвАђвАЂЎ®ЎѓўИвАђ вАЂўКўИЎђЎѓвАђ. 11)вАЂЎЂвАђвАЂЎ±вАђвАЂўБўКЎЂЎІЎЇўИвАђвАЂўЕЎ™ЎЈЎІЎ®ўВЎ©вАђ вАЂўКЎ∞ўГЎ±вАђ. 12)вАЂЎІўИўКЎ©вАђвАЂЎ≤вАђвАЂўДўДвАђвАЂЎІўЕўДЎЂўДЎЂўКЎ©вАђ вАЂЎІўДўЖЎ≥Ў®вАђ вАЂЎ•ўКЎђЎІЎѓвАђ вАЂўБўКвАђвАЂЎЂвАђвАЂЎ±вАђвАЂўБўКЎЂЎІЎЇўИвАђ вАЂўЕЎ™ЎЈЎІЎ®ўВЎ©вАђ вАЂўКЎ≥Ў™ЎЃЎѓўЕвАђ. 13)вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂўЕўДЎђўЕўИЎєвАђ вАЂЎІўЕўДЎЂўДЎЂўКЎ©вАђ вАЂЎІўДўЖЎ≥Ў®вАђ вАЂЎ•ўДўКЎђЎІЎѓвАђвАЂЎІўЕўДЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂўВўИЎІўЖўКўЖвАђ вАЂўКЎ≥Ў™ЎЃЎѓўЕвАђ. 14)вАЂЎІўИўКЎ™ўКвАђвАЂЎ≤вАђ вАЂЎ®ўКўЖвАђ вАЂўВвАђвАЂўДўДўБЎ±вАђ вАЂЎІўЕўДЎЂўДЎЂўКЎ©вАђ вАЂЎІўДўЖЎ≥Ў®вАђ вАЂЎ•ўДўКЎђЎІЎѓвАђвАЂЎІўЕўДЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂўВўИЎІўЖўКўЖвАђ вАЂўКЎ≥Ў™ЎЃЎѓўЕвАђвАЂўЖвАђ.
- 4. вАЂЎІўДЎ™ЎєўДўКўЕўКЎ©вАђ вАЂЎІўДўИЎ≥ЎІЎ¶ўДвАђ.. вАЂЎђўЗЎІЎ≤вАђвАЂЎІЎҐўДўКЎ®ЎІЎѓвАђ. вАЂЎ®ЎЈЎІўВЎІЎ™вАђ. вАЂЎІўДўИЎ≠ЎѓЎ©вАђ вАЂЎѓЎІЎ¶Ў±Ў©вАђ вАЂўДўИЎ≠Ў©вАђ. Mulit mouses вАЂЎ©вАђвАЂЎ±вАђвАЂЎ≥Ў®ўИвАђ вАЂЎ£ўВЎІўДўЕвАђ
- 5. вАЂЎІўДЎђЎѓўКЎѓЎ©вАђ вАЂўИЎІўЕўДўБЎІўЗўКўЕвАђ вАЂЎІўЕўДўБЎ±ЎѓЎІЎ™вАђ.. *вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂўЕЎђўЕўИЎєвАђ вАЂЎђўКЎ®вАђ *вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂЎ®ўКўЖвАђ вАЂўВвАђвАЂЎІўДўБЎ±вАђ вАЂЎђўКЎ®вАђ *вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђвАЂўЕЎђўЕўИЎєвАђ вАЂЎ™ўЕЎІўЕвАђ вАЂЎђўКЎ®вАђ *вАЂЎІўИўКЎ™ўКўЖвАђвАЂЎ≤вАђ вАЂЎ®ўКўЖвАђ вАЂўВвАђвАЂЎІўДўБЎ±вАђ вАЂЎ™ўЕЎІўЕвАђ вАЂЎђўКЎ®вАђ *вАЂўЕЎ™ўГЎІўБЎ¶Ў©вАђ вАЂЎѓўИЎІўДвАђ
- 6. вАЂЎІўДЎ™ЎЈЎ®ўКўВвАђ вАЂЎІўДЎ™ЎѓЎ±ўКЎ≥вАђ вАЂЎІўДўЕўИЎґўИЎєвАђ вАЂЎІўДЎ≠ЎµЎ©вАђ вАЂЎ£ўЖвАђ вАЂЎ≠ЎІўИўДвАђ вАЂЎІўДЎЈЎІўДЎ®вАђ вАЂўГЎ™ЎІЎ®вАђ вАЂЎ™Ў≠ўДвАђ1,2 вАЂЎµвАђ вАЂЎІўДЎЈЎІўДЎ®вАђ вАЂўГЎ™ЎІЎ®вАђ100 вАЂўЕЎЂЎІўДвАђ1 вАЂЎµвАђ101вАЂўЕЎЂЎІўДвАђ2 вАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђвАЂЎІўДЎѓўИЎІўДвАђ вАЂЎІўДўЕЎ™ўГЎІўБЎ¶Ў©вАђ вАЂЎІЎ£ўДўИўДўКвАђ вАЂЎІўДЎ™ўЕЎІЎ±ўКўЖвАђ вАЂўГЎ±ЎІЎ≥Ў©вАђ вАЂЎµвАђ40вАЂЎ±ўВўЕвАђ вАЂўЕўЖвАђ1вАЂЎІўДўКвАђ вАЂЎ±ўВўЕвАђ3,вАЂЎ±ўВўЕвАђ вАЂўИўЕўЖвАђ6 вАЂЎ±ўВўЕвАђ вАЂЎІўДўКвАђ10 вАЂЎІўДЎЈЎІўДЎ®вАђ вАЂўГЎ™ЎІЎ®вАђ вАЂЎµвАђ102вАЂўЕЎЂЎІўДвАђ3, вАЂЎ™Ў≠ўДвАђ вАЂЎ£ўЖвАђ вАЂЎ≠ЎІўИўДвАђ3 вАЂўГЎ±ЎІЎ≥Ў©вАђвАЂЎІўДЎ™ўЕЎІЎ±ўКўЖвАђ вАЂЎµвАђ40вАЂЎ±ўВўЕвАђ5 вАЂЎІўДўЕЎђўЕўИЎєвАђ вАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂЎ®ўКўЖвАђ вАЂўИЎІўДўБЎ±ўВвАђвАЂЎ≤ЎІўИўКЎ™ўКвАђвАЂўЖвАђ вАЂЎІўДЎЂЎІўЖўКЎ©вАђ вАЂЎІўДЎ™ўЕЎІЎ±ўКўЖвАђ вАЂўГЎ±ЎІЎ≥Ў©вАђ вАЂЎµвАђ40вАЂЎ±ўВўЕвАђ4 вАЂЎµвАђ вАЂЎІўДЎЈЎІўДЎ®вАђ вАЂўГЎ™ЎІЎ®вАђ103 вАЂўЕЎЂЎІўДвАђ4,вАЂЎ™Ў≠ўДвАђ вАЂЎ£ўЖвАђ вАЂЎ≠ЎІўИўДвАђ 4 вАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂЎ™ЎІЎ®ЎєвАђ вАЂЎ®ўКўЖвАђ вАЂўИЎІўДўБЎ±ўВвАђ вАЂЎІўДўЕЎђўЕўИЎєвАђ вАЂЎ≤ЎІўИўКЎ™ўКўЖвАђ вАЂЎІўДЎЂЎІўДЎЂЎ©вАђ вАЂўДвАђвАЂЎІўДЎђЎѓўИвАђвАЂўКЎєвАђвАЂЎ≤вАђвАЂўДЎ™ўИвАђ вАЂЎІўЕўДўВЎ™Ў±Ў≠вАђ вАЂЎІўДЎ≠ЎµЎµвАђ..
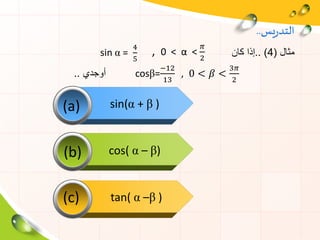
- 9. вАЂўКЎ≥вАђвАЂЎ±вАђвАЂЎІўДЎ™ЎѓвАђ.. вАЂЎІўДўЕЎ™ўГЎІўБЎ¶Ў©вАђ вАЂЎІўДЎѓўИЎІўДвАђ вАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂЎІЎ£ўДЎ≥ЎІЎ≥ўКЎ©вАђ вАЂЎІўДўЕЎЂўДЎЂўКЎ©вАђ вАЂЎІўДЎѓўИЎІўДвАђ вАЂЎ®ўКўЖвАђ вАЂЎІўДўЕЎ™ўГЎІўБЎ¶Ў©вАђ вАЂЎІўДЎѓўИЎІўДвАђ вАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ вАЂЎ™Ў±Ў®ЎЈвАђ вАЂўДўЗЎІвАђ вАЂЎІўДўЕўГЎІўБЎ¶Ў©вАђ вАЂўИЎІўДЎѓўИЎІўДвАђ (вАЂЎІўДЎ™ўЕЎІўЕвАђ вАЂўИЎЄўДвАђ вАЂўИЎІўДЎЄўДвАђ вАЂЎІўДЎ™ўЕЎІўЕвАђ вАЂўИЎђўКЎ®вАђ вАЂЎІўДЎђўКЎ®вАђ,вАЂЎІўДЎ™ўЕЎІўЕвАђ вАЂўИўВЎІЎЈЎєвАђ вАЂЎІўДўВЎІЎЈЎєвАђ)
- 10. вАЂўЕЎЂЎІўДвАђ(1..) sin (пБ± - рЭЬЛ 2 ) = - cos пБ± вАЂЎ£ўЖвАђ вАЂЎ£ЎЂЎ®Ў™вАђ: вАЂЎІўДЎ≠ўДвАђ.. Sin (пБ± - рЭЬЛ 2 ) = sin пБЫ - ( рЭЬЛ 2 - пБ± ) пБЭ b вАУ a = - ( a вАУ b ) = - sin ( рЭЬЛ 2 - пБ± ) sin (- пБ°) = - sin (пБ° ) = - cos пБ± sin ( рЭЬЛ 2 - пБ° ) = cos
- 11. вАЂўЕЎЂЎІўДвАђ(2..) cos(пБ± - рЭЬЛ 2 ) = sinпБ± вАЂЎ£ўЖвАђ вАЂЎ£ЎЂЎ®Ў™вАђ: вАЂЎІўДЎ≠ўДвАђ.. cos (пБ± - рЭЬЛ 2 ) = cos пБЫ - ( рЭЬЛ 2 - пБ± ) пБЭ b вАУ a = - ( a вАУ b ) = cos ( рЭЬЛ 2 - пБ± ) cos (- пБ°) = cos (пБ° ) = sin пБ± cos( рЭЬЛ 2 - пБ° ) = sin пБ°
- 12. вАЂўЕЎЂЎІўДвАђ(3..) Csc (пБ± - рЭЬЛ 2 ) = - sec пБ± вАЂЎ£ўЖвАђ вАЂЎ£ЎЂЎ®Ў™вАђ: вАЂЎІўДЎ≠ўДвАђ.. csc (пБ± - рЭЬЛ 2 ) = csc пБЫ - ( рЭЬЛ 2 - пБ± ) пБЭ b вАУ a = - ( a вАУ b ) = 1 рЭС†рЭСЦрЭСЫвИТ( рЭЬЛ 2 вИТрЭЬГ) = 1 вИТsin ( рЭЬЛ 2 вИТрЭЬГ) sin ( - пБ° ) = - sin пБ° = вИТ1 рЭСРрЭС†рЭСРрЭЬГ = - sec пБ± sin ( рЭЬЛ 2 - пБ° ) = cos пБ°
- 13. вАЂўЕЎЂЎІўДвАђ(4..) sec (пБ± - рЭЬЛ 2 ) = csc пБ± вАЂЎ£ўЖвАђ вАЂЎ£ЎЂЎ®Ў™вАђ: вАЂЎІўДЎ≠ўДвАђ.. sec(пБ± - рЭЬЛ 2 ) = sec пБЫ - ( рЭЬЛ 2 - пБ± ) пБЭ = b вАУ a = - ( a вАУ b ) 1 cos[вИТ рЭЬЛ 2 вИТрЭЬГ ] = = 1 cos( рЭЬЛ 2 вИТрЭЬГ ) cos( - пБ° ) = cos пБ° = 1 рЭС†рЭСЦрЭСЫрЭЬГ = csc пБ± cos ( рЭЬЛ 2 - пБ° ) = sin пБ°
- 15. вАЂЎІўДЎ≥ўДўИўГўКЎ©вАђ вАЂЎІЎ£ўДўЗЎѓЎІўБвАђ..вАЂўЕўЖвАђ3-10 вАЂЎ≥вАђвАЂЎ±вАђвАЂЎІўДЎѓвАђ вАЂЎ™ўЕўЗўКЎѓвАђ.. вАЂЎµўБЎ±ўКўКўЖвАђвАЂЎЇўКЎ±вАђ вАЂўЕўДЎ™ЎђўЗўКўЖвАђ вАЂЎІўДЎѓЎІЎЃўДўКвАђ вАЂЎІўДЎґЎ±Ў®вАђ вАЂўЖЎІЎ™ЎђвАђвАЂЎ£ўЖвАђ вАЂЎ™ЎєўДўЕЎ™вАђ рЭРі= < XA,YA > ,рЭРµ =<XB ,YB> вАЂЎ•ўКЎђЎІЎѓўЗвАђ вАЂўКўЕўГўЖвАђвАЂЎ®Ў•Ў≠ЎѓўЙвАђвАЂЎІўДЎ™ЎІўДўКЎ™ўКўЖвАђ вАЂЎІўДЎєЎІўДўВЎ™ўКўЖвАђ: рЭРівИЩ рЭРµ = XAXB + YAYB рЭРівИЩ рЭРµ =а•• рЭРіа••вИЩа•• рЭРµа••cosќЄ вАЂЎ≠ўКЎЂвАђќЄвАЂЎ®ЎІўЕўДЎ™ЎђўЗўКўЖвАђ вАЂЎІўЕўДЎ≠ЎѓЎѓЎ©вАђ вАЂЎІўИўКЎ©вАђвАЂЎ≤вАђвАЂЎІўДвАђвАЂўЗўКвАђ.
- 16. вАЂўКЎ≥вАђвАЂЎ±вАђвАЂЎІўДЎ™ЎѓвАђ.. вАЂўЕЎ™ЎЈЎІЎ®ўВЎ©вАђ вАЂЎ•ўДўКЎђЎІЎѓвАђ вАЂўЕўДЎ™ЎђўЗўКўЖвАђ вАЂЎІўДЎѓЎІЎЃўДўКвАђвАЂЎІўДЎґЎ±Ў®вАђ вАЂўЖЎ≥Ў™ЎЃЎѓўЕвАђ вАЂЎ≥ўИўБвАђ cos (ќ± вАУ ќ≤) рЭСВрЭСБ вИЩ рЭСВрЭСБ = <cosќ≤ ,sinќ≤ >вИЩ<cosќ± , sinќ± > = cosќ≤cosќ±+sinќ≤sinќ± вА¶(1) рЭСВрЭСБ вИЩ рЭСВрЭСБ =а••рЭСВрЭСБа••вИЩа••рЭСВрЭСБа••cos(ќ≤ вАУќ±) =1 √Ч 1 √Ч cos(ќ≤ вАУќ±) =cos(ќ≤ вАУќ±) рЭСВрЭСБ вИЩ рЭСВрЭСБ = cos(ќ≤ вАУќ±) вА¶(2)
- 17. вАЂўЕўЖвАђ(1)вАЂўИвАђ(2): cos(ќ≤ вАУќ±) = cosќ≤cosќ±+sinќ≤sinќ± вАЂўИЎІўДўКЎђЎІЎѓвАђcos(ќ≤ +ќ±) ќ≤ +ќ± = ќ≤ вАУ (- ќ±) cos( ќ≤ +ќ±) =cos[ ќ≤ вАУ (- ќ±)] =cosќ≤cos(-ќ±)+sinќ≤sin(-ќ±) =cosќ≤cosќ±+sinќ≤(-sinќ±) cos( ќ≤ +ќ±)= cosќ≤cosќ±-sinќ≤sinќ±
- 18. вАЂўГЎ™ЎІЎ®Ў©вАђ вАЂўЖЎ≥Ў™ЎЈўКЎєвАђsin (ќ≤+ќ±)вАЂЎІўДЎіўГўДвАђ вАЂЎєўДўЙвАђ(ќ≤+ќ±) ]-cos[ рЭЬЛ 2 Sin(ќ≤+ќ±) = cos[ рЭЬЛ 2 -(ќ≤ +ќ±) ] = cos[( рЭЬЛ 2 вАУ ќ≤ - ќ± ] = cos[( рЭЬЛ 2 - ќ≤) - ќ± ] =cos( рЭЬЛ 2 - ќ≤)cosќ± + sin ( рЭЬЛ 2 - ќ≤)sinќ± Sin(ќ≤ + ќ±) =sin ќ≤ cosќ± + cosќ≤ sinќ± Sin(ќ≤-ќ±)= sin[ ќ≤+(-ќ±)] = sin ќ≤ cos(-ќ±) + cosќ≤ sin(-ќ±) Sin(ќ≤ - ќ±) =sin ќ≤ cosќ± - cosќ≤ sinќ±
- 19. вАЂЎ®ўГЎ™ЎІЎ®Ў©вАђtan(ќ≤ + ќ±) = sin(рЭЫљ+рЭЫЉ) cos(рЭЫљ+рЭЫЉ) вАЂЎєўДўЙвАђ вАЂўЖЎ≠ЎµўДвАђ.. tan(ќ≤ + ќ±) = рЭС°рЭСОрЭСЫрЭЫљ+рЭС°рЭСОрЭСЫрЭЫЉ 1вИТрЭС°рЭСОрЭСЫрЭЫљрЭС°рЭСОрЭСЫрЭЫЉ tan(ќ≤ - ќ±) = рЭС°рЭСОрЭСЫрЭЫљвИТрЭС°рЭСОрЭСЫрЭЫЉ 1+рЭС°рЭСОрЭСЫрЭЫљрЭС°рЭСОрЭСЫрЭЫЉ
- 20. вАЂўИЎІўДўБЎ±ўВвАђ вАЂЎІўДўЕЎђўЕўИЎєвАђ вАЂўЕЎ™ЎЈЎІЎ®ўВЎІЎ™вАђ.. cos(ќ≤ вАУ ќ±) = cosќ≤cosќ± + sinќ≤sinќ± cos( ќ≤ + ќ±)= cosќ≤cosќ± - sinќ≤sinќ± Sin(ќ≤ + ќ±) =sin ќ≤ cosќ± + cosќ≤ sinќ± Sin(ќ≤ - ќ±) =sin ќ≤ cosќ± - cosќ≤ sinќ± tan(ќ≤ + ќ±) = рЭС°рЭСОрЭСЫрЭЫљ+рЭС°рЭСОрЭСЫрЭЫЉ 1вИТрЭС°рЭСОрЭСЫрЭЫљ рЭС°рЭСОрЭСЫрЭЫЉ tan(ќ≤ - ќ±) = рЭС°рЭСОрЭСЫрЭЫљвИТрЭС°рЭСОрЭСЫрЭЫЉ 1+рЭС°рЭСОрЭСЫрЭЫљ рЭС°рЭСОрЭСЫрЭЫЉ
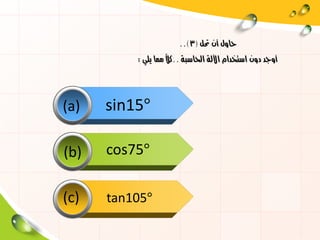
- 21. вАЂЎІЎ£ўДўЕЎЂўДЎ©вАђ.. вАЂўЕЎЂЎІўДвАђ(3)вАЂЎµвАђ102 вАЂўКўДўКвАђ вАЂўЕўЕЎІвАђ ўЛвАЂЎІўДвАђвАЂўГвАђ вАЂЎІўДЎ≠ЎІЎ≥Ў®Ў©вАђ вАЂЎІЎҐўДўДЎ©вАђ вАЂЎІЎ≥Ў™ЎЃЎѓЎІўЕвАђ вАЂЎѓўИўЖвАђ вАЂЎ£ўИЎђЎѓвАђ.. (a) Cos15¬∞ (b) sin105¬∞ (c) tan75¬∞
- 22. (a)Cos15¬∞ = cos(60¬∞ - 45¬∞)= =cos60¬∞cos45¬∞+sin60¬∞sin45¬∞ = 1 2 √Ч 2 2 + 3 2 √Ч 2 2 = 2 4 + 6 4 = 2+ 6 4
- 26. (a)sin15¬∞= sin(60¬∞ -45¬∞) =sin60¬∞cos45¬∞- cos60¬∞sin45¬∞ = 3 2 √Ч 2 2 вИТ 1 2 √Ч 2 2 = 6вИТвИЪ2 4
- 27. (b)cos75¬∞= cos(45¬∞+30¬∞)= =cos45¬∞cos30¬∞-sin45¬∞sin30¬∞ = 2 2 √Ч 3 2 вИТ 2 2 √Ч 1 2 = 6вИТ 2 4
- 28. (c)tan105¬∞= tan(60¬∞+45¬∞)= = рЭС°рЭСОрЭСЫ60¬∞+рЭС°рЭСОрЭСЫ45¬∞ 1вИТрЭС°рЭСОрЭСЫ60¬∞рЭС°рЭСОрЭСЫ45¬∞ = 3+1 1вИТ 3√Ч1 = 3+1 1вИТ 3 √Ч 1+ 3 1+ 3 = 2 3+4 вИТ 2 = вИТ2 вИТ 3
- 30. вАЂЎІўДЎ≥ўДўИўГўКЎ©вАђ вАЂЎІЎ£ўДўЗЎѓЎІўБвАђ..вАЂўЕўЖвАђ11-14 вАЂЎ≥вАђвАЂЎ±вАђвАЂЎІўДЎѓвАђ вАЂЎ™ўЕўЗўКЎѓвАђ.. ўЛвАЂЎІўДвАђвАЂЎ£ўИвАђ..вАЂЎ™ўЕЎ±ўКўЖвАђ вАЂўЕўЖЎІўВЎіЎ©вАђ(5)вАЂўИвАђ(7)вАЂўИвАђ(8)вАЂЎµвАђ40вАЂЎІўДЎ™ўЕЎІЎ±ўКўЖвАђ вАЂўГЎ±ЎІЎ≥Ў©вАђ вАЂўЕўЖвАђ.. вАЂЎІўДЎ≤ЎІўИўКЎ©вАђ вАЂЎЄўДвАђ вАЂЎ£ўИвАђ вАЂЎ™ўЕЎІўЕвАђ вАЂЎђўКЎ®вАђ вАЂЎ£ўИвАђ вАЂЎђўКЎ®вАђ вАЂЎµўИЎ±Ў©вАђ вАЂЎєўДўЙвАђ вАЂЎІўДўЕўВЎѓЎІЎ±вАђ вАЂЎІўГЎ™Ў®вАђ.. (5) sin42¬∞cos17¬∞ - cos42¬∞sin17¬∞= sin(42 вАУ 17 )= sin25 (8) cos рЭЬЛ 7 рЭСРрЭСЬрЭС†рЭС• + рЭС†рЭСЦрЭСЫ рЭЬЛ 7 рЭС†рЭСЦрЭСЫрЭС• = cos рЭЬЛ 7 вИТ рЭС• (7) рЭС°рЭСОрЭСЫ19+рЭС°рЭСОрЭСЫ47 1вИТрЭС°рЭСОрЭСЫ19рЭС°рЭСОрЭСЫ47 =tan(19+47 )=tan66 ўЛвАЂЎІвАђвАЂЎЂЎІўЖўКвАђ..вАЂўБўКЎЂЎІЎЇўИЎ±ЎЂвАђ вАЂЎ®ўЕЎ™ЎЈЎІЎ®ўВЎ©вАђ вАЂЎІўДЎЈЎІўДЎ®ЎІЎ™вАђ вАЂЎ™Ў∞ўГўКЎ±вАђ.. Sin2ќ± +cos2ќ± = 1
- 31. (a) (b) (c) вАЂўКЎ≥вАђвАЂЎ±вАђвАЂЎІўДЎ™ЎѓвАђ.. вАЂўЕЎЂЎІўДвАђ(4.. )вАЂЎ•Ў∞ЎІвАђвАЂўГЎІўЖвАђsin ќ± = 4 5 вАЂЎ£ўИЎђЎѓўКвАђ.. cosќ≤= вИТ12 13 , 0 < рЭЫљ < 3рЭЬЛ 2 , 0 < ќ± < рЭЬЛ 2 sin(ќ± + ќ≤ ) cos( ќ± вАУ ќ≤) tan( ќ± вАУќ≤ )
- 32. ўЛвАЂЎІўДвАђвАЂЎ£ўИвАђ..вАЂўЖўИЎђЎѓвАђ:cosќ± ,sinќ≤ , tanќ± ,tanќ≤ вАЂўБўКЎЂЎІЎЇўИЎ±ЎЂвАђ вАЂўЕЎ™ЎЈЎІЎ®ўВЎ©вАђ вАЂЎ®ЎІЎ≥Ў™ЎЃЎѓЎІўЕвАђ Sin2ќ± +cos2ќ± = 1 ( 4 5 )2+ cos2ќ± = 1 cos2ќ± = 1- 16 25 cos2ќ± = 9 25 0 < ќ± < рЭЬЛ 2 cos ќ± > 0 cosќ± = 3 5
- 33. sin2ќ≤ +cos2ќ≤ = 1 sin2 ќ≤ +( вИТ12 13 )2 =1 sin2ќ≤ = 1- 144 169 sin2ќ≤ = 25 169 0 < рЭЫљ < 3рЭЬЛ 2 sinќ≤ <0 sinќ≤ = вИТ5 13 tan ќ± = рЭС†рЭСЦрЭСЫрЭЫЉ рЭСРрЭСЬрЭС†рЭЫЉ = 4 5 3 5 tan ќ± = 4 3
- 34. (a) sin (ќ± +ќ≤ ) = рЭС†рЭСЦрЭСЫрЭЫЉ рЭСРрЭСЬрЭС†рЭЫљ + рЭСРрЭСЬрЭС†рЭЫЉ рЭС†рЭСЦрЭСЫрЭЫљ = 4 5 √Ч вИТ12 13 + 3 5 √Ч вИТ5 13 = вИТ48 65 вИТ 15 65 = вИТ63 65
- 35. (b) cos(ќ± вАУ ќ≤) = рЭСРрЭСЬрЭС†рЭЫЉрЭСРрЭСЬрЭС†рЭЫљ + рЭС†рЭСЦрЭСЫрЭЫЉ рЭС†рЭСЦрЭСЫрЭЫљ = 3 5 √Ч вИТ12 13 + 4 5 √Ч вИТ5 13 = вИТ36 65 вИТ 20 65 = - 56 65
- 36. (c)tan (ќ± вАУќ≤) = tan рЭЫЉвИТtan рЭЫљ 1+tan рЭЫЉ рЭС°рЭСОрЭСЫрЭЫљ = 4 3 вИТ 5 12 1+ 4 3 √Ч 5 12 = 33 56
- 37. вАЂЎ™Ў≠ўДвАђ вАЂЎ£ўЖвАђ вАЂЎ≠ЎІўИўДвАђ)4.. ( вАЂЎІўДўЕЎЂЎІўДвАђ вАЂўЕўЖвАђ вАЂЎІўДўЕЎєЎЈўКЎІЎ™вАђ вАЂЎ®ЎІЎ≥Ў™ЎЃЎѓЎІўЕвАђ)4(вАЂўКўДўКвАђ вАЂўЕўЕЎІвАђ ўЛвАЂЎІўДвАђвАЂўГвАђ вАЂЎ£ўИЎђЎѓвАђ: (a)cos(ќ± +ќ≤) = cosќ± cosќ≤ вАУ sinќ± sinќ≤ = 3 2 √Ч вИТ12 13 вИТ 4 5 √Ч вИТ5 13 = - 1,076
- 38. (a)tan (ќ± +ќ≤ )= рЭС°рЭСОрЭСЫрЭЫЉ+рЭС°рЭСОрЭСЫрЭЫљ 1вИТрЭС°рЭСОрЭСЫрЭЫЉ рЭС°рЭСОрЭСЫрЭЫљ = 4 3 + 5 12 1вИТ 4 3 √Ч 5 12 = 3,93 (a)sin ( ќ≤ вАУ ќ± ) = sin ќ≤ cosќ± вАУ cosќ≤ sinќ± = вИТ5 13 √Ч 3 2 - вИТ12 13 √Ч 4 5 = 0,161










![вАЂўЕЎЂЎІўДвАђ(4..)
sec (пБ± -
рЭЬЛ
2
) = csc пБ± вАЂЎ£ўЖвАђ вАЂЎ£ЎЂЎ®Ў™вАђ:
вАЂЎІўДЎ≠ўДвАђ..
sec(пБ± -
рЭЬЛ
2
) =
sec пБЫ - (
рЭЬЛ
2
- пБ± ) пБЭ = b вАУ a = - ( a вАУ b )
1
cos[вИТ
рЭЬЛ
2
вИТрЭЬГ ]
=
=
1
cos(
рЭЬЛ
2
вИТрЭЬГ )
cos( - пБ° ) = cos пБ°
=
1
рЭС†рЭСЦрЭСЫрЭЬГ
= csc пБ± cos (
рЭЬЛ
2
- пБ° ) = sin пБ°](https://image.slidesharecdn.com/random-140518113622-phpapp01/85/-13-320.jpg)



![вАЂўЕўЖвАђ(1)вАЂўИвАђ(2):
cos(ќ≤ вАУќ±) = cosќ≤cosќ±+sinќ≤sinќ±
вАЂўИЎІўДўКЎђЎІЎѓвАђcos(ќ≤ +ќ±)
ќ≤ +ќ± = ќ≤ вАУ (- ќ±)
cos( ќ≤ +ќ±) =cos[ ќ≤ вАУ (- ќ±)]
=cosќ≤cos(-ќ±)+sinќ≤sin(-ќ±)
=cosќ≤cosќ±+sinќ≤(-sinќ±)
cos( ќ≤ +ќ±)= cosќ≤cosќ±-sinќ≤sinќ±](https://image.slidesharecdn.com/random-140518113622-phpapp01/85/-17-320.jpg)
![вАЂўГЎ™ЎІЎ®Ў©вАђ вАЂўЖЎ≥Ў™ЎЈўКЎєвАђsin (ќ≤+ќ±)вАЂЎІўДЎіўГўДвАђ вАЂЎєўДўЙвАђ(ќ≤+ќ±) ]-cos[
рЭЬЛ
2
Sin(ќ≤+ќ±) = cos[
рЭЬЛ
2
-(ќ≤ +ќ±) ]
= cos[(
рЭЬЛ
2
вАУ ќ≤ - ќ± ]
= cos[(
рЭЬЛ
2
- ќ≤) - ќ± ]
=cos(
рЭЬЛ
2
- ќ≤)cosќ± + sin (
рЭЬЛ
2
- ќ≤)sinќ±
Sin(ќ≤ + ќ±) =sin ќ≤ cosќ± + cosќ≤ sinќ±
Sin(ќ≤-ќ±)= sin[ ќ≤+(-ќ±)]
= sin ќ≤ cos(-ќ±) + cosќ≤ sin(-ќ±)
Sin(ќ≤ - ќ±) =sin ќ≤ cosќ± - cosќ≤ sinќ±](https://image.slidesharecdn.com/random-140518113622-phpapp01/85/-18-320.jpg)