![E = e1 + e2 + … + e55
ek = {(t1[k]-z1[k]) + (t2[k]-z2[k]) }
Z1
Z2
t1
t2
z1
z2
出?層
k番?の
画像
計算
出? 理想値
2 2](https://image.slidesharecdn.com/casuallearningmachinelearningwithexcelno6-200821101241/85/Casual-learning-machine-learning-with_excel_no6-19-320.jpg)
![……
k番?
1番?
55番?
学習データ
ニューラルネット
e1 = {(t1[1]-z1[1]) + (t2[1]-z2[1]) }
2
ek = {(t1[k]-z1[k]) + (t2[k]-z2[k]) }
e55 = {(t1[55]-z1[55]) + (t2[55]-z2[55]) }
2 2
2 2
……
……
誤差
2
予測値の算出](https://image.slidesharecdn.com/casuallearningmachinelearningwithexcelno6-200821101241/85/Casual-learning-machine-learning-with_excel_no6-22-320.jpg)
![……
k番?
1番?
55番?
学習データ
ニューラルネット
e1 = {(t1[1]-z1[1]) + (t2[1]-z2[1]) }
2
ek = {(t1[k]-z1[k]) + (t2[k]-z2[k]) }
e55 = {(t1[55]-z1[55]) + (t2[55]-z2[55]) }
2 2
2 2
……
……
誤差
2
0
0
1
……
正解
t1[1]=1
t2[1]=0
t1[k]=1
t2[k]=0
t1[55]=0
t2[55]=1
……
理想値
予測値の算出](https://image.slidesharecdn.com/casuallearningmachinelearningwithexcelno6-200821101241/85/Casual-learning-machine-learning-with_excel_no6-23-320.jpg)
![……
k番?
1番?
55番?
e1 = {(t1[1]-z1[1]) + (t2[1]-z2[1]) }
2 2
ek = {(t1[k]-z1[k]) + (t2[k]-z2[k]) }
e55 = {(t1[55]-z1[55]) + (t2[55]-z2[55]) }
2 2
2 2
……
……
0
0
1
……
学習データ 誤差
ニューラルネット
予測値の算出
正解
t1[1]=1
t2[1]=0
t1[k]=1
t2[k]=0
t1[55]=0
t2[55]=1
……
理想値
E = e1 + e2 + … + e55
?的関数](https://image.slidesharecdn.com/casuallearningmachinelearningwithexcelno6-200821101241/85/Casual-learning-machine-learning-with_excel_no6-24-320.jpg)
Casual learning machine learning with_excel_no6
- 1. カジュアル勉強会 @仙台 Excelで機械学習入門 第6回 株式会社 エクテック データサイエンティスト
- 3. 前段
- 8. Excel 2013, 2016 Google Spreadsheets
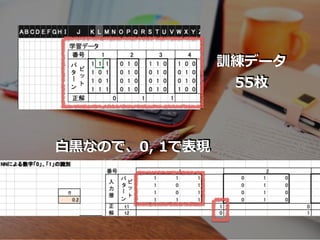
- 14. 4 ? 3 画素の??２値画像として読み取った 「0」,「1」の?書き?字画像を識別する ニューラルネットワークを作成します。 学習?画像データは55枚とします。
- 15. 前回のお话で
- 17. 训练データは55枚あるので
- 18. … {t1, t2} … 正解ラベルtの組は55個ある (今回は”0”,”1”の数字データなので 学習の際にあらかじめ ”0” or “1”の ラベルがふられている) {t1, t2} {t1, t2} {t1, t2}
- 19. E = e1 + e2 + … + e55 ek = {(t1[k]-z1[k]) + (t2[k]-z2[k]) } Z1 Z2 t1 t2 z1 z2 出?層 k番?の 画像 計算 出? 理想値 2 2
- 22. …… k番? 1番? 55番? 学習データ ニューラルネット e1 = {(t1[1]-z1[1]) + (t2[1]-z2[1]) } 2 ek = {(t1[k]-z1[k]) + (t2[k]-z2[k]) } e55 = {(t1[55]-z1[55]) + (t2[55]-z2[55]) } 2 2 2 2 …… …… 誤差 2 予測値の算出
- 23. …… k番? 1番? 55番? 学習データ ニューラルネット e1 = {(t1[1]-z1[1]) + (t2[1]-z2[1]) } 2 ek = {(t1[k]-z1[k]) + (t2[k]-z2[k]) } e55 = {(t1[55]-z1[55]) + (t2[55]-z2[55]) } 2 2 2 2 …… …… 誤差 2 0 0 1 …… 正解 t1[1]=1 t2[1]=0 t1[k]=1 t2[k]=0 t1[55]=0 t2[55]=1 …… 理想値 予測値の算出
- 24. …… k番? 1番? 55番? e1 = {(t1[1]-z1[1]) + (t2[1]-z2[1]) } 2 2 ek = {(t1[k]-z1[k]) + (t2[k]-z2[k]) } e55 = {(t1[55]-z1[55]) + (t2[55]-z2[55]) } 2 2 2 2 …… …… 0 0 1 …… 学習データ 誤差 ニューラルネット 予測値の算出 正解 t1[1]=1 t2[1]=0 t1[k]=1 t2[k]=0 t1[55]=0 t2[55]=1 …… 理想値 E = e1 + e2 + … + e55 ?的関数
- 27. 勾配降下法の式を书き下すと
- 28. ?的関数Eにおいて、重み w11, …,w11, …と 閾値 θ1, … ,θ1, … を順に w11+Δw11, …, θ1+Δθ1, … H H H H w11+Δw11, …, θ1+Δθ1, … O O O O H O H O と変化させたときに?的関数Eが最も?さく なるのは次の関係が成り?つときである (w11, … , θ1, … , w11, …, θ1, …) = - η( H H O O δE δw11 δE δθ1 δE δw11 δE δθ1 H OH O,…, ,…, ,…, ,… )
- 30. そこで 誤差逆伝播法の登場
- 31. そもそも?的関数Eは 平?誤差の和 E = e1 + e2 + … + e55
- 32. そもそも?的関数Eは 平?誤差の和 E = e1 + e2 + … + e55 つまり?的関数Eの勾配は、 平?誤差の和の勾配
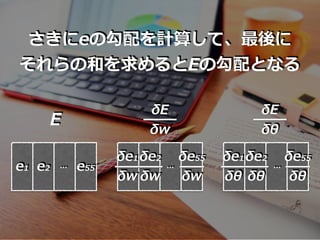
- 33. そもそも?的関数Eは 平?誤差の和 E = e1 + e2 + … + e55 つまり?的関数Eの勾配は、 平?誤差の和の勾配 さきにeの勾配を計算して、最後に それらの和を求めるとEの勾配となる
- 35. ここで 『ユニットの誤差』の導?
- 37. ?的関数Eにおいて、重み w11, …,w11, …と 閾値 θ1, … ,θ1, … を順に w11+Δw11, …, θ1+Δθ1, … H H H H w11+Δw11, …, θ1+Δθ1, … O O O O H O H O と変化させたときに?的関数Eが最も?さく なるのは次の関係が成り?つときである (w11, … , θ1, … , w11, …, θ1, …) = - η( H H O O δE δw11 δE δθ1 δE δw11 δE δθ1 H OH O,…, ,…, ,…, ,… ) ユニットごとに、ユニット間の 重みや閾値を計算しようとするから ?変なことになる
- 39. 1. ユニットの誤差ξの導? 2. 勾配を、ユニットの誤差ξから算出 3. 出?層の『ユニットの誤差』を算出 4. 誤差逆伝播法から中間層の ? 『ユニット誤差』を求める
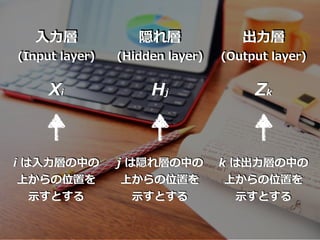
- 41. Xi Hj Zk 隠れ層 (Hidden layer) ??層 (Input layer) 出?層 (Output layer) i は??層の中の 上からの位置を ?すとする j は隠れ層の中の 上からの位置を ?すとする k は出?層の中の 上からの位置を ?すとする
- 42. Hj Zk Xi ユニットXi の出?xi ユニットHj の出?hj ユニットZkの出?zk ??字は、ユニット名を ??字は、ユニットの出?変数を表すことにします
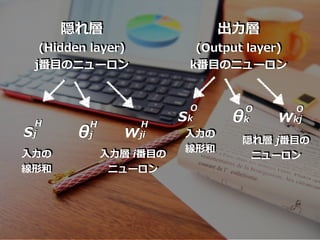
- 43. sj 隠れ層 (Hidden layer) j番?のニューロン 出?層 (Output layer) k番?のニューロン ??の 線形和 H θj H wji H ??層 i番?の ニューロン sk ??の 線形和 O θk O wkj O 隠れ層 j番?の ニューロン
- 44. 1. ユニットの誤差ξの導? δe δsj ξj = (j=1,2,3) δe δsk , ξj = (k=1,2)OH
- 45. 1. ユニットの誤差ξの導? δe δsj ξj = (j=1,2,3) δe δsk , ξk = (k=1,2)OH 2. 勾配を、ユニットの誤差ξから算出 δe δwji H = ξj xi , H δe δθj H = -ξj H (i=1,2, …, 12, j=1,2,3) δe δwkj O = ξk hj , O δe δθk O = -ξk O (j=1,2,3, k=1,2)
- 46. 3. 出?層の『ユニットの誤差』を算出 ξk = O δe δsk O = δe δzk δzk δsk O = δe δzk = a(sk) O
- 47. 3. 出?層の『ユニットの誤差』を算出 ξk = O δe δsk O = δe δzk δzk δsk O = δe δzk = a(sk) O ??で、 e = 1/2{(t1-z1) + (t2-z2) }2 2 なので、※計算のしやすさから 1/2倍している δe δz1 = -(t1 - z1), δe δz2 = -(t2 - z2)
- 48. 3. 出?層の『ユニットの誤差』を算出 ξk = O δe δsk O = δe δzk δzk δsk O = δe δzk = a(sk) O より δe δz1 = -(t1 - z1), δe δz2 = -(t2 - z2) ξ1 = -(t1 - z1) a(s1), ξ2 = -(t2 - z2) a(s2), O OO O
- 49. 3. 出?層の『ユニットの誤差』を算出 ξk = O δe δsk O = δe δzk δzk δsk O = δe δzk = a(sk) O より δe δz1 = -(t1 - z1), δe δz2 = -(t2 - z2) ξ1 = -(t1 - z1) a(s1), ξ2 = -(t2 - z2) a(s2), O OO O 既知の値なので誤差 ξk O が求まる
- 50. 4. 誤差逆伝播法から中間層の ? 『ユニット誤差』を求める ※算出を実際にトライしてみてください ξj = (ξ1w1j + ξ2w2j ) a(sj) (i=1,2,3) H O O O O H
- 51. 4. 誤差逆伝播法から中間層の ? 『ユニット誤差』を求める ※算出を実際にトライしてみてください ξj = (ξ1w1j + ξ2w2j ) a(sj) (i=1,2,3) H O O O O H この仕組みによって、 ?倒な微分計算を?わず、 漸化式で解くことが可能となる
- 53. これが 誤差逆伝播法
- 54. 误差逆伝播法を贰虫肠别濒で体験
- 56. 1. 訓練データの準備
- 58. 2. 重みと閾値の初期化
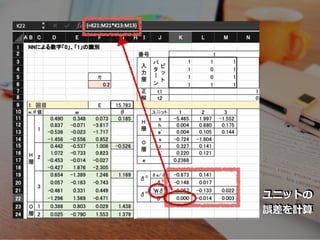
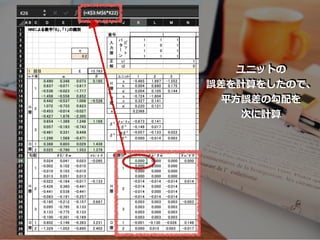
- 63. ユニットの 誤差を計算
- 64. 5.平?誤差e の勾配を計算
- 67. 55枚分を 横にコピペ
- 71. 8. 3.~7.を繰り返し計算
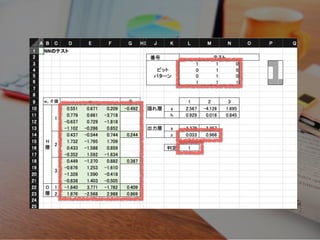
- 73. いざ、テスト
- 75. いかがでしたでしょうか？
- 78. EoF