�ݺ�ߣ

KEL_2_Jembatan_Arus_Bolak_Balik_pptx.pptx

JEMBATAN ARUS BOLAK-BALIK
Disampaikan untuk memenuhi Tugas Mata Kuliah Alat
Ukur dan Metoda Pengukuran Fisika Tahun 2015
Home
Pengertian
Macam-Macam
Jembatan Hay
Jembatan Maxwell
Jembatan Schering
Kondisi Tidak Setimbang
Jembatan Wien
KEL. 2 :
1. VISKIA MANELZA
2. PUTRI ANGJELINA
3. NOVRIZAL SAPUTRA

Arus rangkaian listrik dari sumber
tegangan dipecah kedalam dua
lintasan yang paralel
Jembatan yang terdiri dari empat lengan
jembatan , sumber eksitasi, dan sebuah detektor
nol dan sumber daya menyalurkan tegangan
bolak-balik ke jembatan
Rangkaian Jembatan
Jembatan
Arus Bolak - Balik

JEMBATA
N ARUS
BOLAK-
BALIK
JEMBATAN
MAXWELL
JEMBATAN
HAY
JEMBATAN
SCHERING
JEMBATAN
WIEN
MACAM-MACAM

JEMBATAN MAXWELL
Ciri-ciri
Untuk menghitung induktansi
dan resistansi yang diseri
dengan induktor
Salah satu lengan perbandingan
mempunyai sebuah tahanan dan
sebuah kapasitansi dalam hubungan
paralel

Gambar
Jembatan Maxwell
Tahanan
Induktansi
Tidak
diketahui
KAPASITANSI
Sumber
Tegangan
Tahanan
Tidak
diketahui

Mengukur induktansi dan
tahanan yang tidak diketahui
Mengukur kumparan dengan Q
menengah (1<Q<10)
JEMBATAN MAXWELL
Fungsi

menurut gambar
PERSAMAAN (8-4a)
3
2
4
1 Z
Z
Z
Z 
1
3
2 Y
Z
Z
Zx 
1
1
1
3
3
2
2
1
C
j
R
Y
R
Z
R
Z





3
2
1 Z
Z
Z
Z x 
diperoleh
dari gambar

menurut gambar











 1
1
3
2
1
C
j
R
R
R
L
j
R
Z x
x
x 

1
3
2
R
R
R
Rx  1
3
2 C
R
R
j
L
j x 
 
1
3
2 C
R
R
Lx 
Pisahkan bagian nyata dan
bagian khayal
Bagian nyata
Bagian khayal

JEMBATAN MAXWELL
Aplikasi
Menghitung induktansi dan

Mempunyai tahanan R1
yang seri dengan kapasitor
standar C1.
Sehingga rangkaian hay lebih
cocok untuk pengukuran Q
tinggi.
Sehingga pada sudut-sudut fasa
yang besar, R1 akan mempunyai
nilai yang sangat rendah.
JEMBATAN HAY
Ciri-ciri

Mengukur kumparan dengan Q
tinggi
Mengukur induktansi dan
JEMBATAN HAY
Fungsi

Gambar
Jembatan Hay
Tahanan
Kapasitansi
Sumber
Tegangan
Induktansi
Tidak
Diketahui
Tahanan
Tidak
Diketahui

1
1
1
C
j
R
Z



2
2 R
Z  3
3 R
Z  x
x
x L
j
R
Z 


3
2
1 Z
Z
Z
Z x 
  3
2
1
1 R
R
L
j
R
C
j
R x
x 

 

3
2
1
1
1
1 R
R
C
L
C
jR
L
R
j
R
R x
x
x
x 





dari gambar

3
2
1
1
1
1 R
R
C
L
C
jR
L
R
j
R
R x
x
x
x 





Pisahkan angka nyata dan
angka khayal
Angka nyata
3
2
1
1 R
R
C
L
R
R x
x 

Angka khayal
x
x
L
R
C
R
1
1




3
2
1
1 R
R
C
L
R
R x
x 
 dan
2
1
2
1
2
3
2
1
2
1
2
1 R
C
R
R
R
C
Rx




di dapat
2
1
2
1
2
1
3
2
1 R
C
C
R
R
Lx



x
x
L
R
C
R
1
1




Q
R
L
R
X
x
x
L
L 




tan
1
1
1
tan
R
C
R
XC
C

 

C
L 
 tan
tan 
1
1
1
R
C
Q


atau
2
1
2
1
2
1
3
2
1 R
C
C
R
R
Lx



 2
1
3
2
1
1 Q
C
R
R
Lx


Gambar jembatan
hay menunjukkan
Tangen sudut
fasa induktif
Tangen sudut
fasa kapasitif

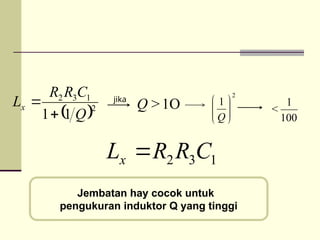
 2
1
3
2
1
1 Q
C
R
R
Lx


1
3
2 C
R
R
Lx 
1O
>
Q
2
1








Q 100
1
<
jika
Jembatan hay cocok untuk
pengukuran induktor Q yang tinggi

JEMBATAN HAY
Aplikasi
Menghitung induktansi dan

Mempunyai tahanan R1
yang paralel dengan
kapasitor C1
JEMBATAN SCHERING
Ciri-ciri

JEMBATAN SCHERING
Untuk pengukuran kapasitor dan
Mengukur sifat-sifat isolasi yakni pada
sudut fasa mendekati 
90
Fungsi

Gambar
Jembatan Schering
Tahanan
Sumber
Tegangan Kapasitansi
Tidak
Diketahui
Tahanan
Tidak
Diketahui

1
3
2 Y
Z
Z
Zx 



















 1
1
3
2
1
C
j
R
C
j
R
C
j
R
x
x 


3
1
2
3
1
2
C
C
R
C
R
jR
C
j
R
x
x 





3
1
2
C
C
R
Rx 
2
1
3
R
R
C
Cx 
Pisahkan angka nyata dan
angka khayal
Angka nyata Angka khayal
Persamaan
Kesetimbangan

x
x
x
x
R
C
X
R
PF 


x
x
x
x
R
C
X
R
D 


Factor daya (PF) dari sebuah
kombinasi seri RC yaitu
cosinus sudut fasa rangkaian
x
x
X
R
PF 
Untuk sudut-sudut fasa yang
sangat mendekati 90◦, reaktansi
hampir sama dengan impedansi
dan dapat mendekati faktor daya
Factor disipasi dari sebuah
rangkaian seri RC
didefinisikan sebagai
cotangent sudut fasa

1
1C
R
D 

3
1
2
C
C
R
Rx 
2
1
3
R
R
C
Cx 
x
x
x
x
R
C
X
R
D 


dengan
didapat

JEMBATAN SCHERING
Untuk pengukuran kapasitor dan
Aplikasi

KONDISI TIDAK SETIMBANG
Tidak terpenuhi
salah satu syarat
kesetimbangan
Jembatan arus bolak-
balik menjadi tidak
setimbang sama sekali

CONTOH 8.3
(HAL.180)
Perhatikan gambar berikut (a) dan tentukan apakah jembatan
tersebut setimbang sempurna atau tidak. Jika tidak, tunjukkan
dua cara agar dia dapat dibuat setimbang dan tetapkan nilai-
nilai numerik untuk setiap komponen tambahan. Anggap
bahwa lengan jembatan 4 adalah yang tidak diketahui yang
tidak dapat diubah.

Penyelesaian
Syarat kesetimbangan :
• Memperbesar
•
3
R
3
2
4
1 


 










90
<
0
90
4
3
2
1



 (Kapasitansi murni)
(Tahanan murni)
(Impedansi induktif)

4
1 
 


 0
3
2 

Akan sedikit negatif
Kesetimbangan
tidak tercapai
Kesetimbangan dapat
dipulihkan
Merubah rangkaian
2 metoda

1. Paralel dengan
kapasitor
1
Z
Kondisi tidak setimbang
Jembatan setimbang
dengan menambah
tahanan pada lengan 1
Menghasilkan
Jembatan maxwell

1
R Ditentukan dengan persamaan
kesetimbangan
3
2
4
1
Z
Z
Z
Y  Dimana
1000
1
1
1
j
R
Y 









5
1000
500
500
100
1000
1
1000
1
1
1
3
2
4
1
R
j
j
R
Z
Z
Z
j
R

2. Mengubah sudut fasa
lengan 2 atau 3 dengan
menserikan kapasitor
dengan persamaan kesetimbangan
2
4
1
3
Z
Z
Z
Z 
 






200
500
500
100
1000
1000
C
C
X
j
j
jX

JEMBATAN WIEN
Mempunyai kombinasi seri
dan paralel RC
Ciri-ciri

JEMBATAN WIEN
Banyak fungsi
Frekuensi
Alat penganalisa distorsi
harmonik
Osilator audio

Gambar
Jembatan Wien
Tahanan
Kapasitansi
Sumber
Tegangan

Memiliki sebuah
kombinasi seri RC dan
sebuah kombinasi
paralel RC

3
2
4
1 Z
Z
Z
Z 
1
1
1
C
j
R
Z



3
3
3
3
1
1
C
j
R
Z
Y 



dengan
3
4
1
3
4
1
2 Y
Z
Z
Z
Z
Z
Z 

persamaan

3
4
1
2 Y
Z
Z
Z 


















 3
3
4
1
1
2
1
C
j
R
R
C
j
R
R 

3
1
4
4
1
4
4
1
3
3
4
1
2
C
C
R
R
C
jR
R
R
C
j
R
R
R
R 






3
1
4
3
4
1
2
C
C
R
R
R
R
R 

3
1
4
4
1
3
R
C
R
R
R
C

 
f

 2

3
1
3
1
2
1
R
R
C
C
f


Pisahkan angka nyata dan angka
khayal
Angka nyata Angka khayal
1
3
3
1
4
2
C
C
R
R
R
R



3
1
3
1
2
1
R
R
C
C
f


3
1 R
R 
3
1 C
C  RC
f

2
1

1
3
3
1
4
2
C
C
R
R
R
R

 4
2 2R
R 
Dalam jembatan praktis,
•C1 dan C3 kapasitor tetap
• R1 dan R3 tahanan variabel yang
Dikontrol oleh sebuah poros bersama
didapat

4
2 2R
R 
Jembatan dapat digunakan
sebagai alat pengukur frekuensi
yang disetimbangkan oleh satu
pengontrol tunggal

DAFTAR PUSTAKA
Bhavani, V. 2008. Measurements And Instrumentation.
Malaysia : IBS BUKU SDN. BHD
William, D Cooper. 1999. Instrumentasi Elektronik Dan Teknik
Pengukuran. Jakarta : Erlangga.
http://www.sentra-edukasi.com/

�ݺ�ߣ

KEL_2_Jembatan_Arus_Bolak_Balik_pptx.pptx

More Related Content

KEL_2_Jembatan_Arus_Bolak_Balik_pptx.pptx