Mammarella
- 1. Valutare lApprendimento della Geometria Irene C. Mammarella Universit degli Studi di Padova
- 3. Geometria nella scuola dellinfanzia La valutazione dellapprendimento della geometria dai 4 ai 6 anni Conosco le Forme: Valutare e potenziare lapprendimento della geometria dai 4 ai 6 anni Lucangeli D., Mammarella I.C., Todeschini M., Miele G., Cornoldi C.
- 4. Geometria nella scuola dellinfanzia Organizzazione delle prove Scuola infanzia e prima classe scuola primaria Conoscenze: Denominazione di figure Differenze tra figure Abilit visuo-spaziali: Classificazione Accoppiamento figure uguali Ricomposizione di figure Colorazione
- 5. Geometria nella scuola dellinfanzia Conoscenze dichiarative Denominazione di figure Differenze tra figure
- 6. Geometria nella scuola dellinfanzia Abilit visuospaziali Accoppiamento e Classificazione di Figure Ricomposizione di Figure Colorazione di Figure
- 7. Geometria nella scuola primaria e secondaria Il GeometriaTest Irene C. Mammarella, Marta Todeschini, Germana Englaro, Daniela Lucangeli & Cesare Cornoldi
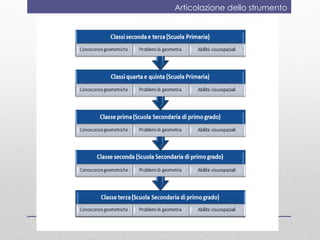
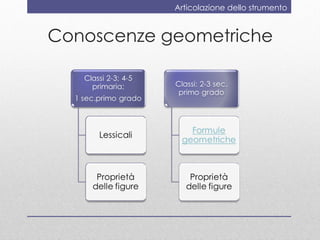
- 9. Articolazione dello strumento Conoscenze geometriche
- 10. Articolazione dello strumento LESSICALE PROPRIETA FIGURE
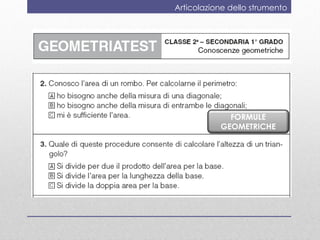
- 11. Articolazione dello strumento FORMULE GEOMETRICHE
- 12. Articolazione dello strumento Problemi geometrici
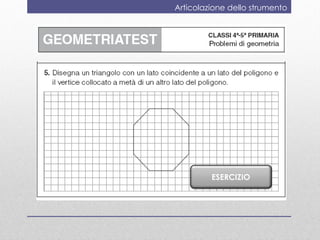
- 13. Articolazione dello strumento ESERCIZIO
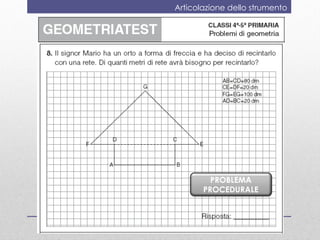
- 14. Articolazione dello strumento PROBLEMA PROCEDURALE
- 15. Articolazione dello strumento PROBLEMA STRATEGICO
- 16. Articolazione dello strumento Abilit visuospaziali 6 sub-test con 4 item a risposta multipla SCOMPOSIZIONE COMPOSIZIONE DI DI FIGURE FIGURE
- 17. Articolazione dello strumento Abilit visuospaziali COMPOSIZIONE DI STIMA DEL FIGURE SOLIDE VOLUME
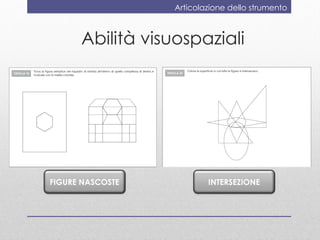
- 18. Articolazione dello strumento Abilit visuospaziali FIGURE NASCOSTE INTERSEZIONE
- 19. Una ricerca sullansia per la matematica e i problemi di geometria
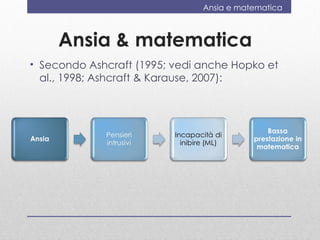
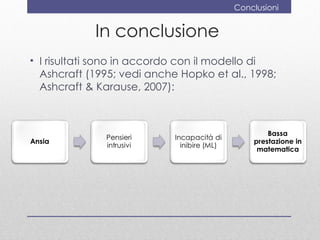
- 20. Ansia e matematica Ansia & matematica Secondo Ashcraft (1995; vedi anche Hopko et al., 1998; Ashcraft & Karause, 2007):
- 21. La Ricerca La presente ricerca Campione iniziale: 100 bambini classe 4 e 5 scuola primaria (52 M 48 F) et media =122.9 mesi (DS=7.46) Materiali: Ansia per la matematica: MARS-R (Saccani & Cornoldi, 2005) Ansia: Test TAD (Barenbaum, et al., 1995) scala A
- 22. Materiali La presente ricerca Prestazioni in geometria - GeometriaTest
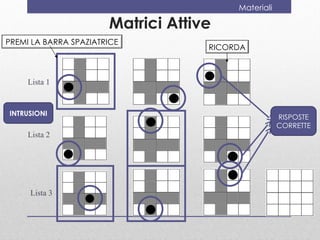
- 23. Materiali Matrici Attive PREMI LA BARRA SPAZIATRICE RICORDA Lista 1 INTRUSIONI RISPOSTE CORRETTE Lista 2 Lista 3
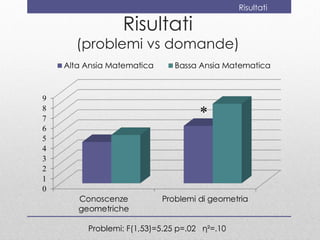
- 26. Risultati Risultati (problemi vs domande) * Problemi: F(1,53)=5.25 p=.02 侶族=.10
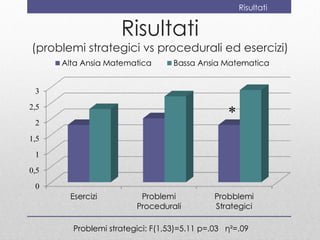
- 27. Risultati Risultati (problemi strategici vs procedurali ed esercizi) * Problemi strategici: F(1,53)=5.11 p=.03 侶族=.09
- 28. Risultati Risultati (Ansia & Problemi & MLVS) Covariando per la percentuale di intrusioni, le differenze tra bambini con alta e bassa ansia nei problemi sono ancora significative? NO Effetto del gruppo F(1,52)=2.38 p=.13 侶族=.04 Effetto della covariata F(1,52)=6.85 p=.01 侶族=.12
- 29. Risultati Quindi In accordo con Ashcraft & Krause (2007) i bambini con alta ansia matematica: Difficolt in problemi geometrici 束strategici損 che coinvolgono la ML Le differenze tra bambini con alta e bassa ansia nella capacit di soluzione di problemi spariscono se si 束ripulisce損 leffetto delle intrusioni in MLVS
- 30. Conclusioni In conclusione I risultati sono in accordo con il modello di Ashcraft (1995; vedi anche Hopko et al., 1998; Ashcraft & Karause, 2007):
- 31. Conclusioni Per la scuola Importante valutare lansia per la matematica Far sperimentare situazioni di successo in prove di geometria
Editor's Notes
- #13: Per esercizio si intende una prova di ragionamento, priva della domanda finale; i problemi procedurali possiedono la struttura tipica dei problemi matematici (presentazione della situazione problema seguita dalla domanda finale) la cui soluzione pu嘆 essere raggiunta attraverso lapplicazione di formule e procedure note allo studente; nei problemi strategici, infine, la conoscenza delle formule e delle procedure, pur essendo necessaria, non 竪 sufficiente per raggiungere il risultato corretto, poich辿 deve intervenire una scoperta da parte dellesecutore ( insight ) che, attraverso un pensiero produttivo, ma sostenuto dal ragionamento, permetta di arrivare alla soluzione.