�ݺ�ߣ

MATRIKS ROTASI DENGAN PUSAT
P (a,b) SEJAUH θ
KELOMPOK 5 XII MIA 2:
-Fitra Rahmadania P
-Iffah Azzah M
-Mutya Eka
-Putri Sagita U
-Resta Astriana
-Tia Uniarti














 








by
ax
by
ax


cossin
sincos
'
'

Catatan Penting
1. Jika titik rotasi sejauh θ searah jarum jam
maka besar sudut = -θ
2. Jika rotasi sejauh θ berlawanan arah jarum
jam maka besar sudut = +θ

Tentukan bayangan titik A (3,2) jika
diputar sejauh 90 berlawanan arah
jarum jam dan berpusat di (4,1)

Matriks rotasi dengan pusat p (a,b)

Jika persamaan bayangan oleh sebuah rotasi
sejauh π/2 searah jarum jam dengan pusat di
P (3,5) adalah 5x-6y + 8 = 0. maka persamaan
mula-mulanya adalah...

Jawab
Persamaan bayangan : 5x’-6y’+ 8 = 0
Karena searah jarum jam maka θ= -π/2
Matriks rotasinya adalah
MR =














































01
10
2
cos
2
sin
2
sin
2
cos



Selanjutnya....























































x
y
y
x
y
x
y
x
by
ax
M
by
ax
R
3
5
5'
3'
5
3
.
01
10
5'
3'
.
'
'
Diperoleh :
x’-3=y-5x’=y-2
y’-5=3-xy’=8-x
Substitusi bayangan :
5x’-6y’+8=0
5(y-2)-6.(8-x)+8=0
5y-10-48+6x+8=0
5y+6x-50=0

tentukan bayangan titik dibawah ini karena
rotasi [P(2,1), R(θ)]
a. A(-3,2), R(30o)

A(-3,2) [P(2,1), R(300)] A’ (x’,y’)














































































 






2
3
3
2
1
2
3
3
2
5
1
2
3
2
1
2
5
2
1
3
2
5
1
2
1
5
3
2
1
2
1
2
1
3
2
1
1
2
12
23
30cos30sin
30sin30cos
'
'
00
00
y
x

B(3,-1) [P(2,1), R(-900)] B’(x’,y’)






























































































0
0
1
2
1
2
1
2
2
1
01
10
1
2
2
1
90cos90sin
90sin90cos
1
2
11
23
)90cos()90sin(
)90sin()90cos(
'
'
oo
oo
oo
oo
y
x

Tuliskan persamaan bayangan kurva di bawah ini
karena rotasi [P, R(θ)]
b. Garis g ≡ y = 3x+2, [P(3,2), R(-30°)]

JAWAB
Bayangan garis g ≡ y = 3x+2 karena [P(3,2), R(-30°)]
Kita akan melakukan dengan cara eliminasi
Gauss-Jordan dalam menjawab soal ini.
Persamaan matriks Gauss-Jordan:























































2'
3'
3
2
1
2
1
2
1
3
2
1
2'
3'
30cos30sin
30sin30cos
2'
3'
)30cos()30sin(
)30sin()30cos(
y
x
y
x
y
x

• Proses Eliminasi Gauss-Jordan:
• (2√3)B1  B1
• (2)B2  B2
(1/3)B1  B1
B1 + B2  B2


















 2'
3'
3
2
1
2
1
2
1
3
2
1
y
x








































4'2
32'3
3
2
31
3
3
1
1
4'2
36'32
31
33
y
x
y
x




































































2
3
3'3
2
1
'
2
1
3
2
1
1'
2
1
'3
6
1
32'3
3
2
10
01
2
3
3'3
2
1
'
2
1
32'3
3
2
10
3
3
1
1
324'2'3
3
2
32'3
3
2
3
3
4
0
3
3
1
1
yx
yxx
yx
x
yx
x
112
22
3
3
1
4
3
BBB
BB









hal ini berarti:
2
1
3'3
2
1
'
2
1
2
3
3'3
2
1
'
2
1
2
43
2
3
'
2
1
'3
2
1
3
2
1
1'
2
1
'3
6
1
32'3
3
2
3




yxy
yxy
yxx
yxxx

Kedua persamaan di atas
disubstitusikan ke persamaan garis
y=3x+2, diperoleh bayangan
0
2
1
133
2
7
'
2
3
3
2
1
'
2
1
3
2
3
014
2
1
3
2
9
3'
2
3
3
2
1
'
2
1
3
2
3
2123
2
9
'
2
3
'3
2
3
2
1
3'3
2
1
'
2
1
243
2
3
'
2
1
'3
2
1
3
2
1
3'3
2
1
'
2
1


































yx
yx
yxyx
yxyx

(kedua ruas dikalikan 2)
Jadi , bayangan garis g adalah
02737')33(')133(  yx
02737')33(')133(  yx

�ݺ�ߣ

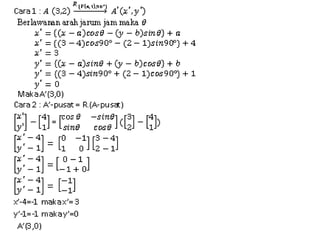
Matriks rotasi dengan pusat p (a,b)

More Related Content

Matriks rotasi dengan pusat p (a,b)