More Related Content
What's hot (20)
More from Inger B辰ckstr旦m (20)
Potenser
- 1. Potenser Potens betyder f旦rm奪ga N奪got som 辰r potent 辰r n奪got med stor f旦rm奪ga, starkt, effektivt Inger B辰ckstr旦m, Burtr辰sk 1
- 2. N奪gon har allts奪 uppfunnit ett effektivt s辰tt att skriva tal p奪 Inger B辰ckstr旦m, Burtr辰sk 2
- 3. Olika typer av potenser: Tal i potensform Tiopotenser Tal i tiopotensform Tal med tiopotenser Grundpotensform Tal i grundpotensform Inger B辰ckstr旦m, Burtr辰sk 3
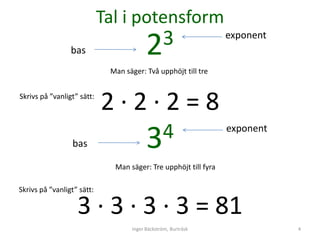
- 4. Tal i potensform bas 2 3 exponent Man s辰ger: Tv奪 upph旦jt till tre Skrivs p奪 vanligt s辰tt: 222=8 bas 3 4 exponent Man s辰ger: Tre upph旦jt till fyra Skrivs p奪 vanligt s辰tt: 3 3 3 3 = 81 Inger B辰ckstr旦m, Burtr辰sk 4
- 5. Tiopotenser bas 102 exponent Man s辰ger: Tio upph旦jt till tv奪 102= 10 10 = 100 Inger B辰ckstr旦m, Burtr辰sk 5
- 6. 10 2= 10 10 = 100 103 = 10 10 10 = 1000 104 = 10 000 106 = 1 000 000 Ser du sambandet mellan exponenten och antalet nollor? Inger B辰ckstr旦m, Burtr辰sk 6
- 7. Tiopotenser tal mindre 辰n 1 En tiondel 0,1 Obs!!! Tal mindre 辰n 1 1 1 har negativ exponent. 10 Om tiorna finns 10 nedanf旦r br奪kstrecket En hundradel 0,01 blir de upph旦jt till minus n奪gonting. 1 100 1 1 1 2 10 100 10 10 102 2 0,01 10 Inger B辰ckstr旦m, Burtr辰sk 7
- 8. Tiopotenser tal mindre 辰n 1 0,001 = 10-3 0,000 001 = 10-6 10-4 = 0,000 1 10-9 = 0,000 000 001 Inger B辰ckstr旦m, Burtr辰sk 8
- 9. Tal i tiopotensform 17 102 198 106 1 435 109 0,01 107 0,398 10-6 Inger B辰ckstr旦m, Burtr辰sk 9
- 10. Grundpotensform I ord: Ett tal mellan 1 och 10 multiplicerat med en tiopotens Med siffror: 6,3 104 6,3 104 = 6,3 10 000 = 63 000 1,8 10-2 1,8 10-2 = 1,8 0,01 = 0,018 Inger B辰ckstr旦m, Burtr辰sk 10
- 11. Fr奪n tal i tiopotensform till tal i grundpotensform 52 102 (tal i tiopotensform) 52 102 = 5 200 Inger B辰ckstr旦m, Burtr辰sk 11
- 12. 52 102 = 5,2 103 Tal mellan 1 och 10 Tiopotens Vad g旦r man f旦r att f奪 52 till ett tal mellan 1 och 10? Inger B辰ckstr旦m, Burtr辰sk 12
- 13. Jo, man delar med 10 52 5,2 10 Men f旦r att beh奪lla v辰rdet p奪 talet, allts奪 5 200, m奪ste man g旦ra n奪got mer Man m奪ste g旦ra tiopotensen st旦rre, man m奪ste multiplicera den med 10: 102 10 = 103 52 102 = 5,2 103 Kontroll: Mindre St旦rre 52 100 = 5 200 5,2 1000 = 5 200 Inger B辰ckstr旦m, Burtr辰sk 13
- 14. Fr奪n tal i tiopotensform till tal i grundpotensform 1,2 10 2 0,12 103 = St旦rre Mindre 0,12 10 10 10 = 1,2 10 10 0,037 105 = 3,7 10 3 St旦rre Mindre Kontroll: 0,037 1010101010 = 3,7 101010 0,037 10 = 0,37 0,37 10 = 3,7 Inger B辰ckstr旦m, Burtr辰sk 14
- 15. Tiopotensform Grundpotensform 2,3 10 -3 23 10-4 = Mindre St旦rre 23 0,0001 = 2,3 0,001 23 2,3 10 0,0001 10 = 0,001 Kontroll: 23 0,000 1 = 0,0023 2,3 0,001 = 0,0023 Inger B辰ckstr旦m, Burtr辰sk 15
- 16. Tiopotensform Grundpotensform -4 0,47 10 -3 = 4,7 10 St旦rre Mindre 0,47 10 = 4,7 0,001 0,0001 10 Kontroll: 0,47 0,001 = 0,00047 4,7 0,0001 = 0,00047 Inger B辰ckstr旦m, Burtr辰sk 16