More Related Content
What's hot (20)
PPT
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П: –Я–µ—А–µ–Љ—Ц—Й–µ–љ–љ—П —В–∞ –є–Њ–≥–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Цsveta7940ћэ
PPT
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц —В–∞ –є–Њ–≥–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц. –У–Њ–Љ–Њ—В–µ—В—Ц—П.sveta7940ћэ
PPT
–Ї–≤–∞–і—А–∞—В–љ–µ —А—Ц–≤–љ—П–љ–љ—П —П–Ї –Љ–∞—В–µ–Љ–∞—В–Є—З–љ–∞ –Љ–Њ–і–µ–ї—М –њ—А–Є–Ї–ї–∞–і–љ–Њ—Ч –Ј–∞–і–∞—З—Цssuserd3e938ћэ
DOC
–Ъ–Њ–љ—В—А–Њ–ї—М–љ–∞ —А–Њ–±–Њ—В–∞ –њ–Њ —В–µ–Љ—Ц " –†–Њ–Ј–≤"—П–Ј—Г–≤–∞–љ–љ—П –Ј–∞–і–∞—З –Ј–∞ –і–Њ–њ–Њ–Љ–Њ–≥–Њ—О —А—Ц–≤–љ—П–љ—М"sveta7940ћэ
PPTX
–≤–њ–Є—Б–∞–љ—Ц –Њ–њ–Є—Б–∞–љ—Ц —З–Њ—В–Є—А–Є–Ї—Г—В–љ–Є–Ї–Є 1Lesya74ћэ
PPT
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–Я–Њ–љ—П—В—В—П –њ–ї–Њ—Й—Ц –Љ–љ–Њ–≥–Њ–Ї—Г—В–љ–Є–Ї–∞. sveta7940ћэ
PPT
–Ъ–Њ–ї–Њ, –Њ–њ–Є—Б–∞–љ–µ –љ–∞–≤–Ї–Њ–ї–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞. –Ъ–Њ–ї–Њ, –≤–њ–Є—Б–∞–љ–µ –≤ —В—А–Є–Ї—Г—В–љ–Є–Ї.sveta7940ћэ
PPTX
–њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П —В–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —Ц –Ї–Њ–љ—Г—Б—Ц–≤.pptxssuser908bb6ћэ
PPT
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–†–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц —З–Є—Б–ї–∞. –Ж—А—А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц —З–Є—Б–ї–∞, –і—Ц–є—Б–љ—Ц —З–Є—Б–ї–∞, —З–Є—Б–ї–Њ–≤—Ц –Љ–љ–Њ...sveta7940ћэ
PPTX
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –і–Њ —Г—А–Њ–Ї—Г вДЦ9 "–Т–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є"kurchenkogalinaћэ
PPT
–Т–ї–∞—Б—В–Є–≤—Ц—Б—В—М —В–Њ—З–Ї–Є, —А—Ц–≤–љ–Њ–≤—Ц–і–і–∞–ї–µ–љ–Њ—Ч –≤—Ц–і —Г—Б—Ц—Е —Б—В–Њ—А—Ц–љ –Љ–љ–Њ–≥–Њ–Ї—Г—В–љ–Є–Ї–∞–Ы—О–і–Љ–Є–ї–∞ –Ъ–Є—А–Є–ї—О–Їћэ
Viewers also liked (20)
PPT
–Њ–±вАЩ—Ф–Љ –Љ–љ–Њ–≥–Њ–≥—А–∞–љ–љ–Є–Ї—Ц–≤ (–љ–∞–≤—З–∞–ї—М–љ–∞ –њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П —В–∞ –Ј–∞–≤–і–∞–љ–љ—П)–Ы—О–і–Љ–Є–ї–∞ –©–µ—Ж–Њ–≤–∞ћэ
PPTX
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –љ–∞ –Ї–Њ–љ–Ї—Г—А—Б —О–љ–Є—Е –Љ–∞—В–µ–Љ–∞—В–Є–Ї—Ц–≤ —Ц–Љ–µ–љ—Ц –Ь.–Т.–Ю—Б—В—А–Њ–≥—А–∞–і—Б—М–Ї–Њ–≥–Њkurchenkogalinaћэ
PPT
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П —Г—А–Њ–Ї—Г –і–Њ –Ї–Њ–љ–Ї—Г—А—Б—Г "–£—З–Є—В–µ–ї—М —А–Њ–Ї—Г" —Г –љ–Њ–Љ—Ц–љ–∞—Ж—Ц—Ч вАЭ–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞вАЭkurchenkogalinaћэ
PPT
–њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –і–Њ —Г—А–Њ–Ї—Г вДЦ1.–њ–Њ—З–∞—В–Ї–Є —В–µ–Њ—А—Ц—Ч –є–Љ–Њ–≤—Ц—А–љ–Њ—Б—В—Ц NataKvashaћэ
PPT
–Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П –Љ–µ—В–∞–љ–Њ–ї—Г –є –µ—В–∞–љ–Њ–ї—Г, —Ч—Е –і—Ц—П –љ–∞ –Њ—А–≥–∞–љ—Ц–Ј–Љ –ї—О–і–Є–љ–Єanakaolesyaћэ
Similar to –≤—З–Є—В–µ–ї—М—Б—М–Ї–∞ –њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –і–Њ —Г—А–Њ–Ї—Г –њ–Њ–і—Ц–±–љ—Ц—Б—В—М –≥–Њ–Љ–Њ—В–µ—В—Ц—П (7)
PPT
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П: –Я–∞—А–∞–ї–µ–ї—М–љ–µ –њ–µ—А–µ–љ–µ—Б–µ–љ–љ—Пsveta7940ћэ
DOC
–Я–Њ–і—Ц–±–љ—Ц—Б—В—М —Д—Ц–≥—Г—А. –Я–ї–Њ—Й—Ц –њ–Њ–і—Ц–±–љ–Є—Е —Д—Ц–≥—Г—Аsveta7940ћэ
PPTX
—Б–Є–Љ–µ—В—А—Ц—П –≤—Ц–і–љ–Њ—Б–љ–Њ —В–Њ—З–Ї–Є —Ц –њ—А—П–Љ–Њ—ЧSv1tsunћэ
More from Lyubow Bondar (20)
DOC
—Г—А–Њ–Ї –Ї–≤–∞–і—А–∞—В–љ—Ц –Ї–Њ—А–µ–љ—Ц —А—Ц–≤–љ—П–љ–љ—ПLyubow Bondarћэ
DOC
—А–Њ–Ј–≤—П–Ј—Г–≤–∞–љ–љ—П —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ–Є—Е —А—Ц–≤–љ—П–љ—М —Й–Њ –Ј–≤–Њ–і—П—В—М—Б—П –і–Њ –Ї–≤–∞–і—А–∞—В–љ–Є—ЕLyubow Bondarћэ
DOC
—Г—А–Њ–Ї –≥—А–∞ –Ї–≤–∞–і—А–∞—В–љ—Ц —А—Ц–≤–љ—П–љ–љ—ПLyubow Bondarћэ
PPS
–Ї—Ц—А–Њ–≤–Њ–≥—А–∞–і вАУ –Љ—Ц–є –Ј–Њ–ї–Њ—В–Є—Б—В–Є–є –Ї—А–∞–єLyubow Bondarћэ
PPT
–Љ–Њ –њ—А–Є—А–Њ–і–љ–Є—З–Њ–Љ–∞—В–µ–Љ–∞—В–Є—З–љ–Њ–≥–Њ —Ж–Є–Ї–ї—ГLyubow Bondarћэ
PPT
–°–Њ—Ж—Ц–∞–ї—М–љ–∞ —Б—Ц—В–Ї–∞. –Ф–Њ–±—А–Њ —Ц –Ј–ї–Њ —Й–Њ –≤–Њ–љ–∞ –≤ —Б–Њ–±—Ц —Е–Њ–≤–∞—Ф..Lyubow Bondarћэ
PPT
—Б–Њ—Ж—Ц–∞–ї—М–љ–Є–є –њ—А–Њ–µ–Ї—В —Г –і–Є—В—П—З–Њ–Љ—Г —Б–∞–і–Њ—З–Ї—ГLyubow Bondarћэ
PPT
–Я–Њ—А—В—Д–Њ–ї—Ц–Њ —В–≤–Њ—А—З–Њ–≥–Њ –≤—З–Є—В–µ–ї—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є —В–∞ —Ц–љ—Д–Њ—А–Љ–∞—В–Є–Ї–ЄLyubow Bondarћэ
DOC
–і–Є—Д–µ—А–µ–љ—Ж—Ц–∞—Ж—Ц—П –њ—А–Є –≤–Є–Ї–ї–∞–і–∞–љ–љ—Ц —Ц–љ—Д–Њ—А–Љ–∞—В–Є–Ї–Є. —Г—З–љ—Ц–≤—Б–Ї–∞ –Ї–Њ–љ—Д–µ—А–µ–љ—Ж—Ц—П.Lyubow Bondarћэ
PPT
Intel ¬Ђ—И–ї—П—Е –і–Њ —Г—Б–њ—Ц—Е—Г¬ї —Б–Њ—Ж—Ц–∞–ї—М–љ–Є–є –њ—А–Њ–µ–Ї—В –Я–∞—А–ЇLyubow Bondarћэ
–≤—З–Є—В–µ–ї—М—Б—М–Ї–∞ –њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –і–Њ —Г—А–Њ–Ї—Г –њ–Њ–і—Ц–±–љ—Ц—Б—В—М –≥–Њ–Љ–Њ—В–µ—В—Ц—П
- 5. –Я—А–Њ–і–Њ–≤–ґ —А–µ—З–µ–љ–љ—ПвА¶.
–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П —Б–Є–Љ–µ—В—А—Ц—Ч –≤—Ц–і–љ–Њ—Б–љ–Њ
—В–Њ—З–Ї–Є –Ю –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —В–∞–Ї–µ вА¶вА¶..
–§—Ц–≥—Г—А–Є F —Г —Д—Ц–≥—Г—А—Г F1, —Г–љ–∞—Б–ї—Ц–і–Њ–Ї
—П–Ї–Њ–≥–Њ –Ї–Њ–ґ–љ–∞ —В–Њ—З–Ї–∞ —Д—Ц–≥—Г—А–Є F
–њ–µ—А–µ—Е–Њ–і–Є—В—М —Г вА¶..—Д—Ц–≥—Г—А–Є F1, вА¶вА¶..
–Т—Ц–і–љ–Њ—Б–љ–Њ —В–Њ—З–Ї–Є –Ю.
–¶—О —Б–Є–Љ–µ—В—А—Ц—О —Й–µ –љ–∞–Ј–Є–≤–∞—О—В—М вА¶..
- 11. –Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П
–њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц.
–У–Њ–Љ–Њ—В–µ—В—Ц—П.
1. –Ю–Ј–љ–∞—З–µ–љ–љ—П –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е
–њ–µ—А–µ—В–≤–Њ—А–µ–љ—М.
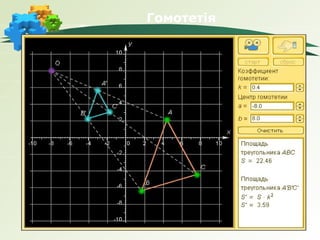
2. –Ъ–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В –≥–Њ–Љ–Њ—В–µ—В—Ц—Ч.
3. –Т–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц –њ–µ—А–µ—В–≤–Њ—А–µ–љ—М.
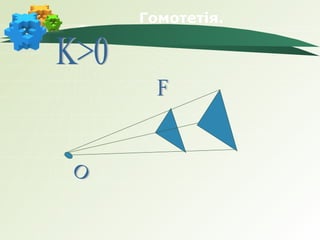
- 12. –У–Њ–Љ–Њ—В–µ—В—Ц—П.
пБґ –У–Њ–Љ–Њ—В–µ—В—Ц—П –Ј —Ж–µ–љ—В—А–Њ–Љ —Г —В–Њ—З—Ж—Ц –Ю —Ц
–Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–Њ–Љ –Ъ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —В–∞–Ї–µ
–≥–µ–Њ–Љ–µ—В—А–Є—З–љ–µ –њ–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П, —П–Ї–µ
–њ–µ—А–µ–≤–Њ–і–Є—В—М –і–Њ–≤—Ц–ї—М–љ—Г —В–Њ—З–Ї—Г –Р —Д—Ц–≥—Г—А–Є F вАУ
–њ—А–Њ–Њ–±—А–∞–Ј—Г –≤ —В–Њ—З–Ї—Г –Р1 —Д—Ц–≥—Г—А–Є F1 вАУ–Њ–±—А–∞–Ј—Г
—В–∞–Ї, —Й–Њ —В–Њ—З–Ї–Є –Р, –Ю, –Р1 –ї–µ–ґ–∞—В—М –љ–∞ –Њ–і–љ—Ц–є
–њ—А—П–Љ—Ц–є —Ц –Р1–Ю= |–Ъ|–Р–Ю
пБґ –°–∞–Љ—Ц —Д—Ц–≥—Г—А–Є –њ—А–Є —Ж—М–Њ–Љ—Г –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П
–≥–Њ–Љ–Њ—В–µ—В–Є—З–љ–Є–Љ–Є.
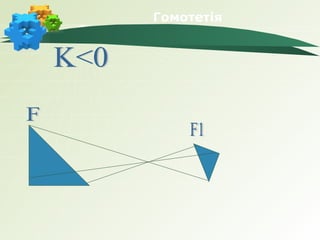
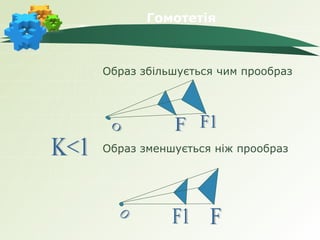
- 13. –У–Њ–Љ–Њ—В–µ—В—Ц—П.
–Т–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц
пБґ –У–Њ–Љ–Њ—В–µ—В—Ц—П –Ј–±–µ—А—Ц–≥–∞—Ф —Д–Њ—А–Љ—Г —Д—Ц–≥—Г—А–Є, –∞–ї–µ –љ–µ —Ч—Ч
—А–Њ–Ј–Љ—Ц—А–Є.
пБґ –У–Њ–Љ–Њ—В–µ—В—Ц—П —Ф –њ–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц.
пБґ –У—А–∞–і—Г—Б–љ–∞ –Љ—Ц—А–∞ –Ї—Г—В—Ц–≤ –њ—А–Є –њ–µ—А–µ—В–≤–Њ—А–µ–љ–љ—Ц
–Ј–±–µ—А—Ц–≥–∞—Ф—В—М—Б—П.
пБґ –Т—Ц–і–њ–Њ–≤—Ц–і–љ—Ц –ї—Ц–љ—Ц–є–љ—Ц –µ–ї–µ–Љ–µ–љ—В–Є –≥–Њ–Љ–Њ—В–µ—В–Є—З–љ–Є—Е
—Д—Ц–≥—Г—А –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ—Ц –Ј –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–Њ–Љ |–Ъ|
пБґ –ѓ–Ї—Й–Њ F ~F1 –Ј –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–Њ–Љ –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц |–Ъ|, —В–Њ
SF1=K2SF
- 18. –У–Њ–Љ–Њ—В–µ—В—Ц—П
–З—Ч –љ–∞–Ј–Є–≤–∞—О—В—М —Ц—Й–µ –∞—Д—Ц–љ–љ–Є–Љ –њ–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П–Љ,
—Г —В–Њ–Љ—Г –≤–Є–њ–∞–і–Ї—Г, —П–Ї—Й–Њ –њ—А—П–Љ—Ц –њ—А–Њ—Е–Њ–і—П—В—М
—З–µ—А–µ–Ј –Њ–і–љ—Г —В–Њ—З–Ї—Г —Ц –њ—А–∞—Ж—О—О—В—М –љ–∞
–Ј–±—Ц–ї—М—И–µ–љ–љ—П.
(–Я—А–Њ–µ–Ї—Ж—Ц–є–љ–Є–є –ї—Ц—Е—В–∞—А, –Ї—Ц–љ–Њ)
- 21. –Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц
–Т–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц
–£ –њ–Њ–і—Ц–±–љ–Є—Е —Д—Ц–≥—Г—А–∞—Е —Г—Б—Ц –ї—Ц–љ—Ц–є–љ—Ц –µ–ї–µ–Љ–µ–љ—В–Є
–њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ—Ц –Ј –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–Њ–Љ –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц –Ъ,
–∞ –Ї—Г—В–Є –Љ—Ц–ґ –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Є–Љ–Є –ї—Ц–љ—Ц–є–љ–Є–Љ–Є
—А–Њ–Ј–Љ—Ц—А–∞–Љ–Є –Ј–±–µ—А—Ц–≥–∞—О—В—М—Б—П.
–Я—А—П–Љ–∞ –њ–µ—А–µ—Е–Њ–і–µ —Г –њ—А—П–Љ—ГвА¶.
–Т—Ц–і–љ–Њ—И–µ–љ–љ—П –і–Њ–≤–ґ–Є–љ –≤—Ц–і—А—Ц–Ј–Ї—Ц–≤ –Њ–і–љ–Њ—Ч –њ—А—П–Љ–Њ—Ч
–Ј–±–µ—А—Ц–≥–∞—Ф—В—М—Б—П.
–Р–Ы–Х
–Т—Ц–і–љ–Њ—И–µ–љ–љ—П –і–Њ–≤–ґ–Є–љ –≤—Ц–і—А—Ц–Ј–Ї—Ц–≤ —А—Ц–Ј–љ–Є—Е
–њ—А—П–Љ–Є—Е, –Э–Х –Ч–С–Х–†–Ж–У–Р–Д–Ґ–ђ–°–ѓ.