–њ–Њ–і–Њ—А–Њ–ґ –і–Њ —Б–µ–Љ–Є —З—Г–і–µ—Б —Б–≤—Ц—В—Г (–≥–µ–Њ–Љ–µ—В—А—Ц—П)
- 1. 1 –Я–Њ–і–Њ—А–Њ–ґ –і–Њ —Б–µ–Љ–Є —З—Г–і–µ—Б —Б–≤—Ц—В—Г.–Я–Њ–і–Њ—А–Њ–ґ –і–Њ —Б–µ–Љ–Є —З—Г–і–µ—Б —Б–≤—Ц—В—Г. –†–Њ–Ј–≤вАШ—П–Ј—Г–≤–∞–љ–љ—П –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є—Е —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤. –Ґ–µ–Њ—А–µ–Љ–∞ –Я—Ц—Д–∞–≥–Њ—А–∞.
- 2. 2 –Ь–µ—В–∞ —Г—А–Њ–Ї—Г :–Ь–µ—В–∞ —Г—А–Њ–Ї—Г : пГЉ –њ–Њ–≤—В–Њ—А–Є—В–Є –Њ–Ј–љ–∞—З–µ–љ–љ—П sinx, cosx, tgx, ctgx –≥–Њ—Б—В—А–Њ–≥–Њ –Ї—Г—В–∞; пГЉ –њ–Њ–≤—В–Њ—А–Є—В–Є —В. –Я—Ц—Д–∞–≥–Њ—А–∞ —В–∞ –Њ—Б–љ–Њ–≤–љ—Ц –љ–∞—Б–ї—Ц–і–Ї–Є –Ј –љ–µ—Ч; пГЉ –Ј–∞–Ї—А—Ц–њ–Є—В–Є –≤–Љ—Ц–љ–љ—П —Ц –љ–∞–≤–Є—З–Ї–Є –Ј–∞—Б—В–Њ—Б–Њ–≤—Г–≤–∞—В–Є —В–µ–Њ—А–µ—В–Є—З–љ–Є–є –Љ–∞—В–µ—А—Ц–∞–ї –і–Њ —А–Њ–Ј–≤вАЩ—П–Ј–∞–љ–љ—П –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є—Е —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤; пГЉ —А–Њ–Ј–≤–Є–љ—Г—В–Є –Љ—Ц–ґ–њ—А–µ–і–Љ–µ—В–љ–Є–є –Ј–≤вАЩ—П–Ј–Њ–Ї (–Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ —В–∞ —Ц—Б—В–Њ—А—Ц—П); пГЉ –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –≤ –њ–Њ–≤—Б—П–Ї–і–µ–љ–љ–Њ–Љ—Г –ґ–Є—В—В—Ц.
- 3. 3 –Ф–µ–≤—Ц–Ј —Г—А–Њ–Ї—Г:–Ф–µ–≤—Ц–Ј —Г—А–Њ–Ї—Г: –ѓ–Ї—Й–Њ —Е–Њ—З–µ—И –і–Њ—Б—П–≥–љ—Г—В–Є –£ –ґ–Є—В—В—Ц —Б–≤–Њ—Ч—Е –≤–µ—А—И–Є–љ, –Ь–∞—В–µ–Љ–∞—В–Є–Ї—Г –Ј–±–∞–≥–љ—Г—В–Є –Ь–∞—Ф—И —В–Њ–љ–Ї–Њ –і–Њ –≥–ї–Є–±–Є–љ.
- 5. 5 –Я–Є—В–∞–љ–љ—П:–Я–Є—В–∞–љ–љ—П: пГЉ –ѓ–Ї –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П —Б—В–Њ—А–Њ–љ–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞? пГЉ –І–Њ–Љ—Г –і–Њ—А—Ц–≤–љ—О—Ф —Б—Г–Љ–∞ –≥–Њ—Б—В—А–Є—Е –Ї—Г—В—Ц–≤ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞? пГЉ –ѓ–Ї –њ–Њ–≤вАЩ—П–Ј–∞–љ—Ц –Љ—Ц–ґ —Б–Њ–±–Њ—О –Ї–∞—В–µ—В–Є —Ц –≥—Ц–њ–Њ—В–µ–љ—Г–Ј–∞ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є—Е —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤? пГЉ –ѓ–Ї—Ц —В—А—Ц–є–Ї–Є —З–Є—Б–µ–ї –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П –њ—Ц—Д–∞–≥–Њ—А–Њ–≤–Є–Љ–Є? пГЉ –ѓ–Ї–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —Ф–≥–Є–њ–µ—В—Б—М–Ї–Є–Љ?
- 6. 6 –Я–Є—В–∞–љ–љ—П: пГЉ –°—Д–Њ—А–Љ—Г–ї—О–є—В–µ –≤–ї–∞—Б—В–Є–≤—Ц—Б—В—М –Љ–µ–і—Ц–∞–љ–Є, –њ—А–Њ–≤–µ–і–µ–љ–Њ—Ч –Ј –≤–µ—А—И–Є–љ–Є –њ—А—П–Љ–Њ–≥–Њ –Ї—Г—В–∞. пГЉ –°—Д–Њ—А–Љ—Г–ї—О–є—В–µ –≤–ї–∞—Б—В–Є–≤—Ц—Б—В—М –Ї–∞—В–µ—В–∞ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞, —Й–Њ –ї–µ–ґ–Є—В—М –њ—А–Њ—В–Є –Ї—Г—В–∞ 30. –Т—Ц–і–њ–Њ–≤—Ц–і—М –њ–Њ—П—Б–љ—Ц—В—М. пГЉ –І–Њ–Љ—Г –і–Њ—А—Ц–≤–љ—О—Ф –≤–Є—Б–Њ—В–∞, –њ—А–Њ–≤–µ–і–µ–љ–∞ –Ј –≤–µ—А—И–Є–љ–Є –њ—А—П–Љ–Њ–≥–Њ –Ї—Г—В–∞? пГЉ –°—Д–Њ—А–Љ—Г–ї—О–є—В–µ –љ–µ—А—Ц–≤–љ—Ц—Б—В—М —В—А–Є–Ї—Г—В–љ–Є–Ї–∞. пГЉ –Ф–∞–є—В–µ –Њ–Ј–љ–∞—З–µ–љ–љ—П sinx, cosx, tgx, ctgx –≥–Њ—Б—В—А–Њ–≥–Њ –Ї—Г—В–∞ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞.
- 9. 9 –Э–∞ –±–µ—А–µ–Ј—Ц —А—Ц—З–Ї–Є –њ–∞–ї—М–Љ–∞ —А–Њ—Б–ї–∞, –Ґ–∞ –≤—Ц—В—А—Г –њ–Њ—А–Є–≤ —Ч—Ч —Б—В–Њ–≤–±—Г—А –Ј–ї–∞–Љ–∞–≤. –Ґ–Њ–њ–Њ–ї—П —Г–њ–∞–ї–∞, —Ц —Б—В–Њ–≤–±—Г—А —Ч—Ч –Ъ—Г—В –њ—А—П–Љ–Є–є –Ј —В–µ—З—Ц—Ф—О —А—Ц—З–Ї–Є —Г—В–≤–Њ—А–Є–≤. –Я–∞–Љ'—П—В–∞–є: –≤ —В–Њ–Љ—Г –Љ—Ц—Б—Ж—Ц —А—Ц–Ї–∞ 4 —Д—Г—В–Є –±—Г–ї–∞ —И–Є—А–Є–љ–Њ—О; –Т–µ—А—Е—Ц–≤–Ї–∞ —Б—Е–Є–ї–Є–ї–∞—Б—М –і–Њ –Ї—А–∞—О, –Ч–∞–ї–Є—И–Є–≤—И–Є 3 —Д—Г—В–∞ –≤—Б—М–Њ–≥–Њ –љ–∞–і –≤–Њ–і–Њ—О. –Я—А–Њ—И—Г —В–µ–њ–µ—А —И–≤–Є–і—И–µ —Б–Ї–∞–ґ–Є –Љ–µ–љ—Ц —В–Є, –Я–∞–ї—М–Љ–∞ —П–Ї–Њ—Ч –±—Г–ї–∞ –≤–Є—Б–Њ—В–Є?
- 11. 11 –£—Б–љ—Ц –Ј–∞–і–∞—З—Ц:–£—Б–љ—Ц –Ј–∞–і–∞—З—Ц: пВі –ѓ–Ї –њ–µ—А–µ–≤—Ц—А–Є—В–Є, —З–Є –Љ–∞—Ф –і–∞–љ–Є–є —И–Љ–∞—В —В–Ї–∞–љ–Є–љ–Є —Д–Њ—А–Љ—Г –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞? пВі –ѓ–Ї –≤—Ц–і –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ—Ч –і–Њ—И–Ї–Є –≤—Ц–і—А—Ц–Ј–∞—В–Є —З–∞—Б—В–Є–љ—Г –њ—Ц–і –Ї—Г—В–Њ–Љ 45 –≥—А–∞–і—Г—Б—Ц–≤ ? пВі –І–Є –Љ–Њ–ґ–љ–∞ –Ј 24 —Б—Ц—А–љ–Є–Ї—Ц–≤ —Б–Ї–ї–∞—Б—В–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї? пВі –ѓ–Ї –Ј–∞ –і–Њ–њ–Њ–Љ–Њ–≥–Њ—О –Љ–Њ—В—Г–Ј–Ї–Є –≤ –°—В–∞—А–Њ–і–∞–≤–љ—М–Њ–Љ—Г –Д–≥–Є–њ—В—Ц –≤—Ц–і–Ї–ї–∞–і–∞–ї–Є –њ—А—П–Љ—Ц –Ї—Г—В–Є?
- 12. 12 –Ь–∞–≤–Ј–Њ–ї–µ–є —Г –У–∞–ї—Ц–Ї–∞—А–љ–∞—Б—Ц–Ь–∞–≤–Ј–Њ–ї–µ–є —Г –У–∞–ї—Ц–Ї–∞—А–љ–∞—Б—Ц
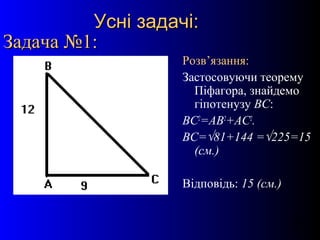
- 13. 13 –£—Б–љ—Ц –Ј–∞–і–∞—З—Ц:–£—Б–љ—Ц –Ј–∞–і–∞—З—Ц: –Ч–∞–і–∞—З–∞ вДЦ1:–Ч–∞–і–∞—З–∞ вДЦ1: –†–Њ–Ј–≤вАЩ—П–Ј–∞–љ–љ—П: –Ч–∞—Б—В–Њ—Б–Њ–≤—Г—О—З–Є —В–µ–Њ—А–µ–Љ—Г –Я—Ц—Д–∞–≥–Њ—А–∞, –Ј–љ–∞–є–і–µ–Љ–Њ –≥—Ц–њ–Њ—В–µ–љ—Г–Ј—Г –Т–°: –Т–°2 =–Р–Т2 +–Р–°2 . –Т–°=вИЪ81+144 =вИЪ225=15 (—Б–Љ.) –Т—Ц–і–њ–Њ–≤—Ц–і—М: 15 (—Б–Љ.)
- 14. 14 –Ч–∞–і–∞—З–∞ вДЦ2–Ч–∞–і–∞—З–∞ вДЦ2 –†–Њ–Ј–≤вАЩ—П–Ј–∞–љ–љ—П: –Ґ—А–Є–Ї—Г—В–љ–Є–Ї –Р–Т–° —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є. (–Р–Т=–Т–°). –Т –љ—М–Њ–Љ—Г –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤–Є—Б–Њ—В–∞ –Т–Ь, —П–Ї–∞ —А—Ц–≤–љ–∞ —Б—В–Њ—А–Њ–љ–∞–Љ –Р–Т —В–∞ –Т–°=> => —В—А–Є–Ї—Г—В–љ–Є–Ї –Р–Ь–Т —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є —В–∞ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–є. –£ —В–∞–Ї–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ –≥–Њ—Б—В—А—Ц –Ї—Г—В–Є —А—Ц–≤–љ—Ц, —В–∞ –і–Њ—А—Ц–≤–љ—О—О—В—М 450 : –°—Г–Љ–∞ –Ї—Г—В—Ц–≤ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ =1800 . –Т –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–Љ—Г —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–Љ—Г: 1800 -(900 +2—Е0 ); —Е0 = 900 /2 =450 . –Т—Ц–і–њ–Њ–≤—Ц–і—М: 450 .
- 15. 15 –Ч–∞–і–∞—З–∞ вДЦ3–Ч–∞–і–∞—З–∞ вДЦ3 –†–Њ–Ј–≤вАЩ—П–Ј–∞–љ–љ—П : –£—Б—Ц —Б—В–Њ—А–Њ–љ–Є –Ї–≤–∞–і—А–∞—В—Г —А—Ц–≤–љ—Ц, —В–∞ –≤—Б—Ц –Ї—Г—В–Є –і–Њ—А—Ц–≤–љ—О—О—В—М 900 . –Я–Њ–і–Є–≤–Є–Љ–Њ—Б—М –љ–∞ —В—А–Є–Ї—Г—В–љ–Є–Ї –Р–°–Ь: вИ†–Р–Ь–°= 900 , –∞ —Б—В–Њ—А–Њ–љ–Є –Р–Ь=–°–Ь. –¶–µ —А—Ц–≤–љ–Њ–±—Ц—З–љ–Є–є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї, –і–Њ –љ—М–Њ–≥–Њ –Љ–Є –Љ–Њ–ґ–µ–Љ–Њ –Ј–∞—Б—В–Њ—Б—Г–≤–∞—В–Є —В–µ–Њ—А–µ–Љ—Г –Я—Ц—Д–∞–≥–Њ—А–∞: –Р–°2 =2–Р–Ь2 ; –Р–Ь2 = –Р–°2 /2; –Р–Ь=вИЪ100/2; –Р–Ь=–Р–°=5вИЪ2 (—Б–Љ). –Т—Ц–і–њ–Њ–≤—Ц–і—М: 5вИЪ2 (—Б–Љ).
- 16. 16 –Ч–∞–і–∞—З–∞ вДЦ4–Ч–∞–і–∞—З–∞ вДЦ4 –†–Њ–Ј–≤вАЩ—П–Ј–∞–љ–љ—П : –Ґ—А–Є–Ї—Г—В–љ–Є–Ї –Р–Т–° –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–є. –Ч–љ–∞–є–і–µ–Љ–Њ –≥—Ц–њ–Њ—В–µ–љ—Г–Ј—Г –Т–° –Ј–∞ —В–µ–Њ—А–µ–Љ–Њ—О –Я—Ц—Д–∞–≥–Њ—А–∞: –Т–°2 =–Р–Т2 +–Р–°2 ; –Т–°=вИЪ64+36 =вИЪ100 = 10 (—Б–Љ). –Ч–љ–∞–є–і–µ–Љ–Њ –њ–ї–Њ—Й—Г —Ж—М–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ –Ј–∞ —Д–Њ—А–Љ—Г–ї–Њ—О:SпБ≤=¬љ –Р–°*–Р–Т; SпБ≤=24—Б–Љ2 . –Ґ–µ–њ–µ—А –Љ–Њ–ґ–µ–Љ–Њ –Ј–љ–∞–є—В–Є —А–∞–і—Ц—Г—Б –Њ–њ–Є—Б–∞–љ–Њ—Ч –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—Ц: R–Њ–њ=–Р–Т*–Т–°*–Р–°/4 SпБ≤; R–Њ–њ =480/96 =5(—Б–Љ). –Т—Ц–і–њ–Њ–≤—Ц–і—М: 5(—Б–Љ).
- 17. 17 –Ч–∞–і–∞—З–∞ вДЦ5:–Ч–∞–і–∞—З–∞ вДЦ5:–†–Њ–Ј–≤вАЩ—П–Ј–∞–љ–љ—П : –Р–Т–°–Ь-—А–Њ–Љ–±. –Т—Б—Ц –є–Њ–≥–Њ —Б—В–Њ—А–Њ–љ–Є —А—Ц–≤–љ—Ц –Љ—Ц–ґ —Б–Њ–±–Њ—О, –і—Ц–∞–≥–Њ–љ–∞–ї—Ц —В–Њ—З–Ї–Њ—О –њ–µ—А–µ—В–Є–љ–∞–љ–љ—П –њ–Њ–і—Ц–ї—П—О—В—М—Б—П –љ–∞–≤–њ—Ц–ї, —В–∞ –њ–µ—А–µ—В–Є–љ–∞—О—В—М—Б—П –њ—Ц–і –њ—А—П–Љ–Є–Љ –Ї—Г—В–Њ–Љ. –Ґ—А–Є–Ї—Г—В–љ–Є–Ї –Р–Ю–Ь –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–є (вИ†–Р–Ю–Ь=900 ). –Ч–љ–∞–є–і–µ–Љ–Њ –≥—Ц–њ–Њ—В–µ–љ—Г–Ј—Г –Р–Ь: –Р–Ь2 =–Ь–Ю2 +–Р–Ю2; –Р–Ь= вИЪ144+256 = вИЪ400 = 20 (—Б–Љ). –Т—Ц–і–њ–Њ–≤—Ц–і—М: 20 (—Б–Љ).
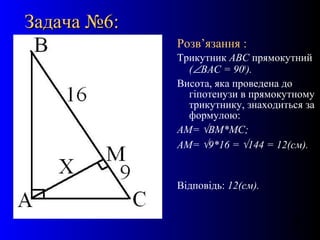
- 18. 18 –Ч–∞–і–∞—З–∞ вДЦ6:–Ч–∞–і–∞—З–∞ вДЦ6: –†–Њ–Ј–≤вАЩ—П–Ј–∞–љ–љ—П : –Ґ—А–Є–Ї—Г—В–љ–Є–Ї –Р–Т–° –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–є (вИ†–Т–Р–° = 900 ). –Т–Є—Б–Њ—В–∞, —П–Ї–∞ –њ—А–Њ–≤–µ–і–µ–љ–∞ –і–Њ –≥—Ц–њ–Њ—В–µ–љ—Г–Ј–Є –≤ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–Љ—Г —В—А–Є–Ї—Г—В–љ–Є–Ї—Г, –Ј–љ–∞—Е–Њ–і–Є—В—М—Б—П –Ј–∞ —Д–Њ—А–Љ—Г–ї–Њ—О: –Р–Ь= вИЪ–Т–Ь*–Ь–°; –Р–Ь= вИЪ9*16 = вИЪ144 = 12(—Б–Љ). –Т—Ц–і–њ–Њ–≤—Ц–і—М: 12(—Б–Љ).
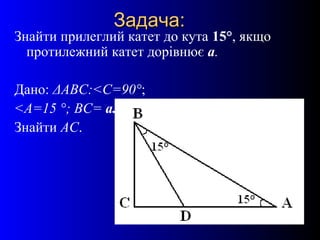
- 19. 19 –Ч–∞–і–∞—З–∞:–Ч–∞–і–∞—З–∞: –Ч–љ–∞–є—В–Є –њ—А–Є–ї–µ–≥–ї–Є–є –Ї–∞—В–µ—В –і–Њ –Ї—Г—В–∞ 15¬∞, —П–Ї—Й–Њ –њ—А–Њ—В–Є–ї–µ–ґ–љ–Є–є –Ї–∞—В–µ—В –і–Њ—А—Ц–≤–љ—О—Ф –∞. –Ф–∞–љ–Њ: ќФ–Р–Т–°:<–°=90¬∞; <–Р=15 ¬∞; –Т–°= –∞. –Ч–љ–∞–є—В–Є –Р–°.
- 20. 20 –†–Њ–Ј–≤'—П–Ј–∞–љ–љ—П –Ј–∞–і–∞—З—Ц:–†–Њ–Ј–≤'—П–Ј–∞–љ–љ—П –Ј–∞–і–∞—З—Ц: пБђ –Я—А–Њ–≤–µ–і–µ–Љ–Њ BD —В–∞–Ї–Є–Љ —З–Є–љ–Њ–Љ, —Й–Њ–± –Ї—Г—В ABD=15¬∞. пБђ ќФABD вАУ —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є: AD=BD (–Ј–∞ –≤–ї–∞—Б—В–Є–≤—Ц—Б—В—О –Ї—Г—В—Ц–≤ —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ <BAD=<ABD). пБђ <BDC вАУ –Ј–Њ–≤–љ—Ц—И–љ—Ц–є –Ї—Г—В, –Ј–∞ —В–µ–Њ—А–µ–Љ–Њ—О –њ—А–Њ –Ј–Њ–≤–љ—Ц—И–љ—Ц–є –Ї—Г—В —В—А–Є–Ї—Г—В–љ–Є–Ї–∞: <BDC=30¬∞. пБђ ќФBDC:<–°=90¬∞. –Ч–∞ –≤–ї–∞—Б—В–Є–≤—Ц—Б—В—О –Ї—Г—В–∞ –њ—А–Њ—В–Є 30¬∞, BD=2B–°=2a. пБђ –Ч–љ–∞–є–і–µ–Љ–Њ DC –Ј–∞ —В–µ–Њ—А–µ–Љ–Њ—О –Я—Ц—Д–∞–≥–Њ—А–∞: DC2=BD2- BC2=4a2-a2=3a2 . пБђ AC=AD+DC=2a+a вИЪ3 =a(2+ вИЪ3 ). пБђ –Т—Ц–і–њ–Њ–≤—Ц–і—М: a(2+вИЪ3).
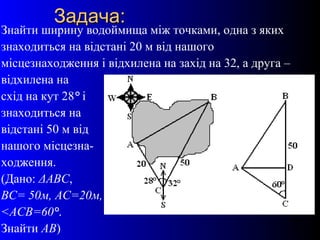
- 22. 22 –Ч–∞–і–∞—З–∞:–Ч–∞–і–∞—З–∞: –Ч–љ–∞–є—В–Є —И–Є—А–Є–љ—Г –≤–Њ–і–Њ–є–Љ–Є—Й–∞ –Љ—Ц–ґ —В–Њ—З–Ї–∞–Љ–Є, –Њ–і–љ–∞ –Ј —П–Ї–Є—Е –Ј–љ–∞—Е–Њ–і–Є—В—М—Б—П –љ–∞ –≤—Ц–і—Б—В–∞–љ—Ц 20 –Љ –≤—Ц–і –љ–∞—И–Њ–≥–Њ –Љ—Ц—Б—Ж–µ–Ј–љ–∞—Е–Њ–і–ґ–µ–љ–љ—П —Ц –≤—Ц–і—Е–Є–ї–µ–љ–∞ –љ–∞ –Ј–∞—Е—Ц–і –љ–∞ 32, –∞ –і—А—Г–≥–∞ вАУ –≤—Ц–і—Е–Є–ї–µ–љ–∞ –љ–∞ —Б—Е—Ц–і –љ–∞ –Ї—Г—В 28¬∞ —Ц –Ј–љ–∞—Е–Њ–і–Є—В—М—Б—П –љ–∞ –≤—Ц–і—Б—В–∞–љ—Ц 50 –Љ –≤—Ц–і –љ–∞—И–Њ–≥–Њ –Љ—Ц—Б—Ж–µ–Ј–љ–∞- —Е–Њ–і–ґ–µ–љ–љ—П. (–Ф–∞–љ–Њ: ќФ–Р–Т–°, –Т–°= 50–Љ, –Р–°=20–Љ, <–Р–°–Т=60¬∞. –Ч–љ–∞–є—В–Є –Р–Т)
- 23. 23 –†–Њ–Ј–≤'—П–Ј–∞–љ–љ—П –Ј–∞–і–∞—З—Ц:–†–Њ–Ј–≤'—П–Ј–∞–љ–љ—П –Ј–∞–і–∞—З—Ц: пБђ –Я—А–Њ–≤–µ–і–µ–Љ–Њ –≤–Є—Б–Њ—В—Г AD: ADвФіBC; пБђ ќФADC: <D= 90¬∞; DC=ACcos60¬∞=20:2=10–Љ; AD=ACsin60¬∞= 20вИЪ3:2=10вИЪ3 –Љ; пБђ BC=CD+BD вАУ –Ј–∞ –∞–Ї—Б—Ц–Њ–Љ–Њ—О –њ–ї–∞–љ—Ц–Љ–µ—В—А—Ц—Ч, —В–Њ–Љ—Г: BD=BC- CD=50-10=40–Љ; пБђ ќФA–ТD: <D=90¬∞вЖТ–Ј–∞ —В–µ–Њ—А–µ–Љ–Њ—О–Я—Ц—Д–∞–≥–Њ—А–∞ A–Т2=AD2+BD2 =300+1600=1900; AB=10вИЪ19–Љ. –Т—Ц–і–њ–Њ–≤—Ц–і—М:10вИЪ19–Љ.
- 24. 24 –Т–Є—Б—П—З—Ц —Б–∞–і–Є –Т–∞–≤—Ц–ї–Њ–љ–∞–Т–Є—Б—П—З—Ц —Б–∞–і–Є –Т–∞–≤—Ц–ї–Њ–љ–∞
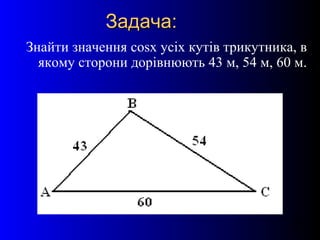
- 25. 25 –Ч–∞–і–∞—З–∞:–Ч–∞–і–∞—З–∞: –Ч–љ–∞–є—В–Є –Ј–љ–∞—З–µ–љ–љ—П cosx —Г—Б—Ц—Е –Ї—Г—В—Ц–≤ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞, –≤ —П–Ї–Њ–Љ—Г —Б—В–Њ—А–Њ–љ–Є –і–Њ—А—Ц–≤–љ—О—О—В—М 43 –Љ, 54 –Љ, 60 –Љ.
- 26. 26 –†–Њ–Ј–≤'—П–Ј–∞–љ–љ—П –Ј–∞–і–∞—З—Ц:–†–Њ–Ј–≤'—П–Ј–∞–љ–љ—П –Ј–∞–і–∞—З—Ц: –Ф–ї—П –Ј–≤–Є—З–∞–є–љ–Є—Е —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤ –Љ–Њ–ґ–µ–Љ–Њ –Ј–∞—Б—В–Њ—Б–Њ–≤—Г–≤–∞—В–Є —В–µ–Њ—А–µ–Љ—Г –Ї–Њ—Б–Є–љ—Г—Б—Ц–≤. –Ф–ї—П —Ж—Ц—Ф—Ч –Ј–∞–і–∞—З—Ц, –њ–Њ-–њ–µ—А—И–µ, –Ј–љ–∞–є–і–µ–Љ–Њ –Ї—Г—В –Р–°–Т –Ј–∞ —В–µ–Њ—А–µ–Љ–Њ—О –Ї–Њ—Б–Є–љ—Г—Б—Ц–≤: –Р–Т2=–Т–°2+–Р–°2-2–Р–Т*–Т–°*cosвИ†–Р–°–Т. –Т–Є—А–∞–Ј–Є–Љ–Њ –Ј —Ж—Ц—Ф—Ч —Д–Њ—А–Љ—Г–ї–Є cosвИ†–Р–°–Т: cosвИ†–Р–°–Т= –Р–Т2 - –Т–°2 - –Р–°2 / 2–Р–Т*–Т–°. –Я—Ц–і—Б—В–∞–≤–ї—П—О—З–Є –Ј–љ–∞—З–µ–љ–љ—П —Б—В–Њ—А—Ц–љ, –Ј–љ–∞–є–і–µ–Љ–Њ cosвИ†–Р–°–Т, –≤—Ц–љ –і–Њ—А—Ц–≤–љ—О—Ф –њ—А–Є–±–ї–Є–Ј–љ–Њ 85 0 . –Р–љ–∞–ї–Њ–≥—Ц—З–љ–Њ –Ј–љ–∞–є–і–µ–Љ–Њ cosвИ†–Р–Т–°. –Т—Ц–љ –і–Њ—А—Ц–≤–љ—О—Ф 75 0 –Ъ—Г—В –°–Р–Т –Ј–љ–∞–є–і–µ–Љ–Њ —В–∞–Ї: —Б—Г–Љ–∞ –≤—Б—Ц—Е –Ї—Г—В—Ц–≤ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ –і–Њ—А—Ц–≤–љ—О—Ф 1800 —В–Њ–Љ—Г –Ї—Г—В –°–Р–Т=1800 вАУ75 0 - 85 0 = 20 0 . –Т—Ц–і–њ–Њ–≤—Ц–і—М: 75 0 ;85 0 ; 20 0.
- 27. 27 –°—М–Њ–≥–Њ–і–љ—Ц –љ–∞ —Г—А–Њ—Ж—Ц –Љ–Є –Ј –≤–∞–Љ–Є:–°—М–Њ–≥–Њ–і–љ—Ц –љ–∞ —Г—А–Њ—Ж—Ц –Љ–Є –Ј –≤–∞–Љ–Є: пГЉ –њ–Њ–≤—В–Њ—А–Є–ї–Є, —Б–Є—Б—В–µ–Љ–∞—В–Є–Ј—Г–≤–∞–ї–Є –є —Г–Ј–∞–≥–∞–ї—М–љ–Є–ї–Є —В–µ–Њ—А–µ—В–Є—З–љ—Ц –њ–Њ–љ—П—В—В—П –Ј –≤–Є–≤—З–µ–љ–Њ—Ч —В–µ–Љ–Є; пГЉ —А–Њ–Ј–≥–ї—П–љ—Г–ї–Є —Г—Б–љ—Ц –≤–њ—А–∞–≤–Є —Ц –Ј–∞–і–∞—З—Ц –њ—А–∞–Ї—В–Є—З–љ–Њ–≥–Њ –Ј–Љ—Ц—Б—В—Г; пГЉ —А–Њ–Ј–≥–ї—П–љ—Г–ї–Є –њ—А–Є–Ї–ї–∞–і–Є –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—П —В–µ–Њ—А–µ–Љ–Є –Я—Ц—Д–∞–≥–Њ—А–∞ –≤ –љ–∞—Г—Ж—Ц, –Љ–Є—Б—В–µ—Ж—В–≤—Ц, –∞—А—Е—Ц—В–µ–Ї—В—Г—А—Ц.