�ݺ�ߣ

‫لالحتمال‬ ‫التقليدى‬ ‫التعريف‬:
‫ف‬ ‫نفسها‬ ‫الفرصه‬ ‫لها‬ ‫نتائجها‬ ‫جميع‬ ‫عشوائيه‬ ‫تجربه‬ ‫لدينا‬ ‫كان‬ ‫إذا‬‫الظهور‬ ‫ى‬
‫العينه‬ ‫فضاء‬ ‫وكان‬S‫عناصره‬ ‫عدد‬ ‫أن‬ ‫أى‬ ‫محدود‬ ‫التجربه‬ ‫لهذه‬n(S)‫قيمه‬
‫الحادث‬ ‫وقوع‬ ‫احتمال‬ ‫فإن‬ ‫محدوده‬A‫عناصره‬ ‫عدد‬ ‫الذى‬n(A)‫يساوى‬
P(A)=n(A)
n(S)
‫مثال‬:‫فردى‬ ‫عدد‬ ‫ظهور‬ ‫احتمال‬ ‫فما‬ ‫واحده‬ ‫مرة‬ ‫متزنه‬ ‫نرد‬ ‫زهرة‬ ‫رميت‬ ‫إذا‬
‫االجابه‬:
S={1,2,3,4,5,6} n(A)={1,3,5}
P(A)=3
6

‫االحتمال�Ĭ ‫بديهيات‬ ‫أو‬ ‫مسلمات‬:
1-‫حادث‬ ‫لكل‬A‫فإن‬P(A) ≥ 0
2-‫واحد‬ ‫يساوى‬ ‫مؤكد‬ ‫حادث‬ ‫وقوع‬ ‫احتمال‬.‫أن‬ ‫أى‬P(S)=1
3-‫اتح‬ ‫احتمال‬ ‫فإن‬ ‫البعض‬ ‫لبعضها‬ ‫مانعه‬ ‫الحوادث‬ ‫كانت‬ ‫إذا‬‫ادها‬
‫احتماالتها‬ ‫مجموع‬ ‫يساوى‬

‫ونتائج‬ ‫نظريات‬
•‫نظريه‬1:‫كان‬ ‫إذا‬Å‫للحادث‬ ‫المتمم‬ ‫الحادث‬ ‫هو‬A‫فإن‬:
• P(Å )=1-P(A)
•‫نتيجه‬:‫احتمال‬‫صفر‬ ‫يساوى‬ ‫مستحيل‬ ‫حادث‬ ‫وقوع‬P(ϕ)=0
•‫نظريه‬2:‫كان‬ ‫إذا‬A,B‫عينه‬ ‫فضاء‬ ‫إلى‬ ‫ينتميان‬ ‫حادثين‬ ‫أى‬
‫فإن‬ ‫محدود‬P(Aᴗ B)=P(A)+(B)+P(A∩B)

‫مثال‬
‫الحادث‬ ‫وكان‬ ‫واحده‬ ‫مره‬ ‫متزنه‬ ‫نرد‬ ‫زهرة‬ ‫رمى‬ ‫تجربه‬ ‫فى‬A‫يمثل‬
‫،والحادث‬ ‫زوجى‬ ‫رقم‬ ‫ظهور‬B‫أويساوى‬ ‫من‬ ‫أقل‬ ‫رقم‬ ‫ظهور‬ ‫يمثل‬
2
‫االجابه‬:‫التجربه‬ ‫لهذه‬ ‫العينه‬ ‫فضاء‬S={1,2,3,4,5,6} n(S)=6
A={2,4,6} B={1,2} A∩B={2}
P(A)=3 P(B)=2 P(A ∩B)=1
6 6 6
P(AᴗB)=3+2-1=4=2
6 6 3

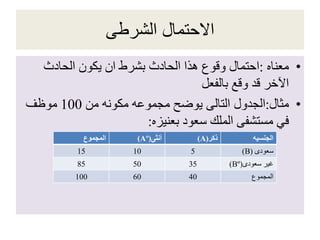
‫االحتمال�Ĭ‫الشرطى‬
•‫معناه‬:‫الحادث‬ ‫يكون‬ ‫ان‬ ‫بشرط‬ ‫الحادث‬ ‫هذا‬ ‫وقوع‬ ‫احتمال‬
‫بالفعل‬ ‫وقع‬ ‫قد‬ ‫اآلخر‬
•‫مثال‬:‫الجدول‬‫التالى‬‫من‬ ‫مكونه‬ ‫مجموعه‬ ‫يوضح‬100‫موظف‬
‫سعود‬ ‫الملك‬ ‫مستشفى‬ ‫في‬‫بعنيزه‬:
‫الجنسيه‬‫ذكر‬(A)‫أنثى‬(Aº)‫المجموع‬
‫سعودى‬)B(51015
‫غير‬‫سعودى‬)Bº(355085
‫المجموع‬4060100

‫االجابه‬
•‫أنثى‬ ‫بأنه‬ ‫علما‬ ‫سعوديا‬ ‫المختار‬ ‫الموظف‬ ‫كان‬ ‫إذا‬
• P(BAº)=n(Aº ∩B) =10
• P(B) 60
•‫نتيجه‬:‫إذا‬‫كان‬P(B)=0‫فإن‬P(AB)‫معرف‬ ‫غير‬ ‫يكون‬

‫الحوادث‬ ‫استقالل‬
•‫معناها‬:‫احتمال‬‫معين‬ ‫حادث‬ ‫وقوع‬A‫اليتأثر‬‫أو‬ ‫بوقوع‬ ‫مطلقا‬
‫آخر‬ ‫حادث‬ ‫وقوع‬ ‫عدم‬B
•‫شروطها‬:1-‫كان‬ ‫إذا‬Aº,B‫مستقالن‬.
•2-‫إذا‬‫كان‬A,Bº‫مستقالن‬.
•3-‫إذا‬‫كان‬Aº,Bº‫مستقالن‬.

‫بيز‬ ‫نظرية‬
‫معين‬ ‫حادث‬ ‫وقوع‬ ‫مصدر‬ ‫هو‬ ‫ما‬ ‫سببا‬ ‫يكون‬ ‫أن‬ ‫احتمال‬ ‫بحساب‬ ‫تعنى‬‫نعلم‬
‫المعر‬ ‫أسبابه‬ ‫أحد‬ ‫وقع‬ ‫إذا‬ ‫يقع‬ ‫الحادث‬ ‫هذا‬ ‫أن‬ ‫حيث‬ ‫بوقوعه‬ ‫مسبقا‬‫وف‬
‫سبب‬ ‫تحقق‬ ‫إذا‬ ‫الحادث‬ ‫هذا‬ ‫وقوع‬ ‫احتمال‬ ‫والمعروف‬ ‫منها‬ ‫كل‬ ‫احتمال‬
‫األسباب‬ ‫هذه‬ ‫من‬ ‫ما‬
P(B ∕ A)=P(A ∕ B).P(B)
P(A)

�ݺ�ߣ

الاحتمال

Recommended

More Related Content

Similar to الاحتمال (15)

More from abeer97 (20)

Recently uploaded (9)

الاحتمال