–≤–Ķ–ļ—ā–ĺ—Ä–ł —Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł —É –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—Ė
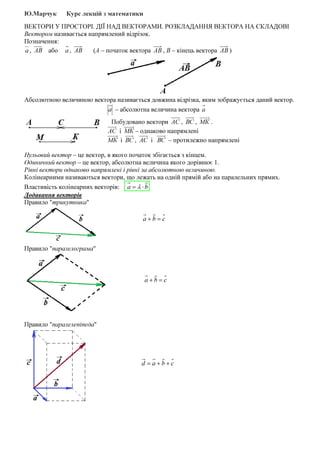
- 1. –ģ.–ú–į—Ä—á—É–ļ –ö—É—Ä—Ā –Ľ–Ķ–ļ—Ü—Ė–Ļ –∑ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł –í–ē–ö–Ę–ě–†–ė –£ –ü–†–ě–°–Ę–ě–†–Ü. –Ē–Ü–á –Ě–ź–Ē –í–ē–ö–Ę–ě–†–ź–ú–ė. –†–ě–ó–ö–õ–ź–Ē–ź–Ě–Ě–Į –í–ē–ö–Ę–ě–†–ź –Ě–ź –°–ö–õ–ź–Ē–ě–í–Ü –í–Ķ–ļ—ā–ĺ—Ä–ĺ–ľ –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –Ĺ–į–Ņ—Ä—Ź–ľ–Ľ–Ķ–Ĺ–ł–Ļ –≤—Ė–ī—Ä—Ė–∑–ĺ–ļ. –ü–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź: –į , –ź–í –į–Ī–ĺ –į , –ź–í (–ź ‚Äď –Ņ–ĺ—á–į—ā–ĺ–ļ –≤–Ķ–ļ—ā–ĺ—Ä–į –ź–í , –í ‚Äď –ļ—Ė–Ĺ–Ķ—Ü—Ć –≤–Ķ–ļ—ā–ĺ—Ä–į –ź–í ) –ź–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—é –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ—é –≤–Ķ–ļ—ā–ĺ—Ä–į –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –ī–ĺ–≤–∂–ł–Ĺ–į –≤—Ė–ī—Ä—Ė–∑–ļ–į, —Ź–ļ–ł–ľ –∑–ĺ–Ī—Ä–į–∂—É—Ē—ā—Ć—Ā—Ź –ī–į–Ĺ–ł–Ļ –≤–Ķ–ļ—ā–ĺ—Ä. –į ‚Äď –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į –į –ü–ĺ–Ī—É–ī–ĺ–≤–į–Ĺ–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł –ź–° , –í–° , –ú–ö . –ź–° —Ė –ú–ö ‚Äď –ĺ–ī–Ĺ–į–ļ–ĺ–≤–ĺ –Ĺ–į–Ņ—Ä—Ź–ľ–Ľ–Ķ–Ĺ—Ė –ú–ö —Ė –í–° , –ź–° —Ė –í–° ‚Äď –Ņ—Ä–ĺ—ā–ł–Ľ–Ķ–∂–Ĺ–ĺ –Ĺ–į–Ņ—Ä—Ź–ľ–Ľ–Ķ–Ĺ—Ė –Ě—É–Ľ—Ć–ĺ–≤–ł–Ļ –≤–Ķ–ļ—ā–ĺ—Ä ‚Äď —Ü–Ķ –≤–Ķ–ļ—ā–ĺ—Ä, –≤ —Ź–ļ–ĺ–≥–ĺ –Ņ–ĺ—á–į—ā–ĺ–ļ –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ –ļ—Ė–Ĺ—Ü–Ķ–ľ. –ě–ī–ł–Ĺ–ł—á–Ĺ–ł–Ļ –≤–Ķ–ļ—ā–ĺ—Ä ‚Äď —Ü–Ķ –≤–Ķ–ļ—ā–ĺ—Ä, –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į —Ź–ļ–ĺ–≥–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē 1. –†—Ė–≤–Ĺ—Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł –ĺ–ī–Ĺ–į–ļ–ĺ–≤–ĺ –Ĺ–į–Ņ—Ä—Ź–ľ–Ľ–Ķ–Ĺ—Ė —Ė —Ä—Ė–≤–Ĺ—Ė –∑–į –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—é –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ—é. –ö–ĺ–Ľ—Ė–Ĺ–Ķ–į—Ä–Ĺ–ł–ľ–ł –Ĺ–į–∑–ł–≤–į—é—ā—Ć—Ā—Ź –≤–Ķ–ļ—ā–ĺ—Ä–ł, —Č–ĺ –Ľ–Ķ–∂–į—ā—Ć –Ĺ–į –ĺ–ī–Ĺ—Ė–Ļ –Ņ—Ä—Ź–ľ—Ė–Ļ –į–Ī–ĺ –Ĺ–į –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł—Ö –Ņ—Ä—Ź–ľ–ł—Ö. –í–Ľ–į—Ā—ā–ł–≤—Ė—Ā—ā—Ć –ļ–ĺ–Ľ—Ė–Ĺ–Ķ–į—Ä–Ĺ–ł—Ö –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤: ba ‚čÖ= őĽ –Ē–ĺ–ī–į–≤–į–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ –ü—Ä–į–≤–ł–Ľ–ĺ "—ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į" cba =+ –ü—Ä–į–≤–ł–Ľ–ĺ "–Ņ–į—Ä–į–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–į" cba =+ –ü—Ä–į–≤–ł–Ľ–ĺ "–Ņ–į—Ä–į–Ľ–Ķ–Ľ–Ķ–Ņ—Ė–Ņ–Ķ–ī–į" cbad ++=
- 2. –í—Ė–ī–Ĺ—Ė–ľ–į–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ cba =‚ąí –ě—Ä—ā ‚Äď —Ü–Ķ –ĺ–ī–ł–Ĺ–ł—á–Ĺ–ł–Ļ –≤–Ķ–ļ—ā–ĺ—Ä, –Ĺ–į–Ņ—Ä—Ź–ľ —Ź–ļ–ĺ–≥–ĺ –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ –Ĺ–į–Ņ—Ä—Ź–ľ–ĺ–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ĺ—ó –ĺ—Ā—Ė. –ü–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –ĺ—Ä—ā—Ė–≤: 1e , 2–Ķ , 3e –į–Ī–ĺ i , j , k 1e ‚Äď –ĺ—Ä—ā –ĺ—Ā—Ė –ě–• –†–ĺ–∑–ļ–Ľ–į–ī–į–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä–į –Ĺ–į —Ā–ļ–Ľ–į–ī–ĺ–≤—Ė —É –Ņ–Ľ–ĺ—Č–ł–Ĺ—Ė yx aaa += –ī–Ķ xa ‚Äď –Ņ—Ä–ĺ–Ķ–ļ—Ü—Ė—Ź –≤–Ķ–ļ—ā–ĺ—Ä–į a –Ĺ–į –≤—Ė—Ā—Ć –ě–•, ya ‚Äď –Ņ—Ä–ĺ–Ķ–ļ—Ü—Ė—Ź –≤–Ķ–ļ—ā–ĺ—Ä–į a –Ĺ–į –≤—Ė—Ā—Ć OY. 1e —Ė xa ‚Äď –ļ–ĺ–Ľ—Ė–Ĺ–Ķ–į—Ä–Ĺ—Ė 2–Ķ —Ė ya ‚Äď –ļ–ĺ–Ľ—Ė–Ĺ–Ķ–į—Ä–Ĺ—Ė, 2–Ķ ‚Äď –ĺ—Ä—ā –ĺ—Ā—Ė OY –Ę–ĺ–ī—Ė 1eax ‚čÖ= őĽ , 2eay ‚čÖ= ¬Ķ . –ě—ā–∂–Ķ, 21 eea ¬ĶőĽ += –†–ĺ–∑–ļ–Ľ–į–ī–į–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä–į –Ĺ–į —Ā–ļ–Ľ–į–ī–ĺ–≤—Ė —É –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—Ė zyx aaaa ++= –ī–Ķ xa ‚Äď –Ņ—Ä–ĺ–Ķ–ļ—Ü—Ė—Ź –≤–Ķ–ļ—ā–ĺ—Ä–į a –Ĺ–į –≤—Ė—Ā—Ć –ě–•, ya ‚Äď –Ņ—Ä–ĺ–Ķ–ļ—Ü—Ė—Ź –≤–Ķ–ļ—ā–ĺ—Ä–į a –Ĺ–į –≤—Ė—Ā—Ć OY, za ‚Äď –Ņ—Ä–ĺ–Ķ–ļ—Ü—Ė—Ź –≤–Ķ–ļ—ā–ĺ—Ä–į a –Ĺ–į –≤—Ė—Ā—Ć OZ. –Ę–ĺ–ī—Ė 1eax ‚čÖ= őĽ , 2eay ‚čÖ= ¬Ķ , 3eaz ‚čÖ=őĹ , 3e ‚Äď –ĺ—Ä—ā –ĺ—Ā—Ė OZ. –ě—ā–∂–Ķ, 321 eeea őŬĶőĽ ++= –ü–†–Į–ú–ě–ö–£–Ę–Ě–Ü –ö–ě–ě–†–Ē–ė–Ě–ź–Ę–ė –í –ü–†–ě–°–Ę–ě–†–Ü. –Ē–Ü–á –Ě–ź–Ē –í–ē–ö–Ę–ě–†–ź–ú–ė, –©–ě –ó–ź–Ē–ź–Ě–Ü –ö–ě–ě–†–Ē–ė–Ě–ź–Ę–ź–ú–ė –ü—Ä–ĺ—Ā—ā–ĺ—Ä–ĺ–≤—É —Ā–ł—Ā—ā–Ķ–ľ—É –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —É—ā–≤–ĺ—Ä—é—é—ā—Ć —ā—Ä–ł –≤–∑–į—Ē–ľ–Ĺ–ĺ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—Ė —á–ł—Ā–Ľ–ĺ–≤—Ė –Ņ—Ä—Ź–ľ—Ė x, y, z, —Ź–ļ—Ė –Ņ–Ķ—Ä–Ķ—ā–ł–Ĺ–į—é—ā—Ć—Ā—Ź –≤ —ā.–ě. –Ę–ĺ—á–ļ–į –ě ‚Äď –Ņ–ĺ—á–į—ā–ĺ–ļ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā. –¶—Ė –Ņ—Ä—Ź–ľ—Ė —É—ā–≤–ĺ—Ä—é—é—ā—Ć –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ—Ė –Ņ–Ľ–ĺ—Č–ł–Ĺ–ł (xy), (yz), (xz). –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł —ā–ĺ—á–ļ–ł –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—É: –ź(x; y; z) x ‚Äď –į–Ī—Ā—Ü–ł—Ā–į, y ‚Äď –ĺ—Ä–ī–ł–Ĺ–į—ā–į, z ‚Äď –į–Ņ–Ľ—Ė–ļ–į—ā–į. –í–ł–Ī–Ķ—Ä–Ķ–ľ–ĺ —É –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä–ĺ–≤—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —ā.–ź. –ü–Ľ–ĺ—Č–ł–Ĺ–į, —Č–ĺ –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā—Ć —á–Ķ—Ä–Ķ–∑ —ā.–ź —Ė –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–į –Ņ–Ľ–ĺ—Č–ł–Ĺ—Ė (yz), –Ņ–Ķ—Ä–Ķ—ā–ł–Ĺ–į—Ē –≤—Ė—Ā—Ć –ě–• –≤ —ā.–ź—Ö; –į–Ĺ–į–Ľ–ĺ–≥—Ė—á–Ĺ–ĺ –≤—Ė—Ā—Ć OY ‚Äď –≤ —ā.–źy, –≤—Ė—Ā—Ć OZ ‚Äď –≤ —ā.–źz. –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ĺ—é —Ö –Ĺ–į–∑–ł–≤–į—é—ā—Ć —á–ł—Ā–Ľ–ĺ, —Ź–ļ–Ķ –∑–į –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—é –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ—é –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –ī–ĺ–≤–∂–ł–Ĺ—Ė –≤—Ė–ī—Ä—Ė–∑–ļ–į –ě–ź—Ö. –Į–ļ—Č–ĺ —ā.–ź—Ö –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ —ā.–ě, —ā–ĺ —Ö = 0. –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ĺ—é y –Ĺ–į–∑–ł–≤–į—é—ā—Ć —á–ł—Ā–Ľ–ĺ, —Ź–ļ–Ķ –∑–į –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—é –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ—é –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –ī–ĺ–≤–∂–ł–Ĺ—Ė –≤—Ė–ī—Ä—Ė–∑–ļ–į –ě–źy. –Į–ļ—Č–ĺ —ā.–źy –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ —ā.–ě, —ā–ĺ y = 0. –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ĺ—é z –Ĺ–į–∑–ł–≤–į—é—ā—Ć —á–ł—Ā–Ľ–ĺ, —Ź–ļ–Ķ –∑–į –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—é –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ—é –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –ī–ĺ–≤–∂–ł–Ĺ—Ė –≤—Ė–ī—Ä—Ė–∑–ļ–į –ě–źz. –Į–ļ—Č–ĺ —ā.–źz –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ —ā.–ě, —ā–ĺ z = 0.
- 3. –ģ.–ú–į—Ä—á—É–ļ –ö—É—Ä—Ā –Ľ–Ķ–ļ—Ü—Ė–Ļ –∑ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł –≤–Ķ–ļ—ā–ĺ—Ä–į —É –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—Ė –∑ –Ņ–ĺ—á–į—ā–ļ–ĺ–ľ –≤ —ā–ĺ—á—Ü—Ė –ź1(x1; y1; z1) —Ė –ļ—Ė–Ĺ—Ü–Ķ–ľ —É —ā–ĺ—á—Ü—Ė A2(x2; y2; z2) –Ĺ–į–∑–ł–≤–į—é—ā—Ć—Ā—Ź —á–ł—Ā–Ľ–į —Ö2 ‚Äď —Ö1, y2 ‚Äď y1, z2 ‚Äď z1. 21AA (—Ö2 ‚Äď —Ö1; y2 ‚Äď y1; z2 ‚Äď z1) –í–Ľ–į—Ā—ā–ł–≤–ĺ—Ā—ā—Ė: ‚ÄĘ —Ä—Ė–≤–Ĺ—Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł –ľ–į—é—ā—Ć —Ä—Ė–≤–Ĺ—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł; ‚ÄĘ –≤–Ķ–ļ—ā–ĺ—Ä–ł –∑ —Ä—Ė–≤–Ĺ–ł–ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł —Ä—Ė–≤–Ĺ—Ė. –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł –ĺ—Ä—ā—Ė–≤: 1e (1; 0; 0), 2–Ķ (0; 1; 0), 3e (0; 0; 1) –Ē—Ė—ó –Ĺ–į–ī –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł ‚ÄĘ –°—É–ľ–ĺ—é –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ –į (–į1; –į2; –į3) —Ė b (b1; b2; b3) –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –≤–Ķ–ļ—ā–ĺ—Ä c ( –į1 +b1; –į2 +b2; –į3 +b3). ‚ÄĘ –Ē–ĺ–Ī—É—ā–ļ–ĺ–ľ –≤–Ķ–ļ—ā–ĺ—Ä–į –į (–į1; –į2; –į3) –Ĺ–į —á–ł—Ā–Ľ–ĺ őĽ –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –≤–Ķ–ļ—ā–ĺ—Ä –įőĽ (őĽ–į1; őĽ–į2; őĽ–į3) –Ě–į–Ņ—Ä—Ź–ľ –≤–Ķ–ļ—ā–ĺ—Ä–į –įőĽ –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ –Ĺ–į–Ņ—Ä—Ź–ľ–ĺ–ľ –≤–Ķ–ļ—ā–ĺ—Ä–į –į , —Ź–ļ—Č–ĺ őĽ > 0, —Ė –Ī—É–ī–Ķ –Ņ—Ä–ĺ—ā–ł–Ľ–Ķ–∂–Ĺ–ł–ľ, —Ź–ļ—Č–ĺ őĽ < 0. –°–ö–ź–õ–Į–†–Ě–ė–ô, –ú–Ü–®–ź–Ě–ė–ô –Ę–ź –í–ē–ö–Ę–ě–†–Ě–ė–ô –Ē–ě–Ď–£–Ę–ö–ė –í–ē–ö–Ę–ě–†–Ü–í –°–ļ–į–Ľ—Ź—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –Ě–Ķ—Ö–į–Ļ –ī–į–Ĺ–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł );;( zyx aaaa —Ė );;( zyx bbbb . –°–ļ–į–Ľ—Ź—Ä–Ĺ–ł–ľ –ī–ĺ–Ī—É—ā–ļ–ĺ–ľ –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —ā–į b –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź —á–ł—Ā–Ľ–ĺ, —Č–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē —Ā—É–ľ—Ė –ī–ĺ–Ī—É—ā–ļ—Ė–≤ —ó—Ö –ĺ–ī–Ĺ–ĺ–Ļ–ľ–Ķ–Ĺ–Ĺ–ł—Ö –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā. ab = –į1b1 + –į2b2 + –į3b3 –°–ļ–į–Ľ—Ź—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —ā–į b –Ņ–ĺ–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ ba ‚čÖ , –į–Ī–ĺ ( )ba, . –ě—ā–∂–Ķ, a ¬∑ b = ( )ba, = ax bx + ay by + az bz . (1) –Ě–Ķ—Ö–į–Ļ ŌÜ ‚ÄĒ –ļ—É—ā –ľ—Ė–∂ –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł a —Ė b , —ā–ĺ–ī—Ė —Ā–ļ–į–Ľ—Ź—Ä–Ĺ–ł–ľ –ī–ĺ–Ī—É—ā–ļ–ĺ–ľ –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —ā–į b —Ē —á–ł—Ā–Ľ–ĺ, —Č–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –ī–ĺ–Ī—É—ā–ļ–ĺ–≤—Ė –ī–ĺ–≤–∂–ł–Ĺ —Ü–ł—Ö –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ –Ĺ–į –ļ–ĺ—Ā–ł–Ĺ—É—Ā –ļ—É—ā–į ŌÜ –ľ—Ė–∂ –Ĺ–ł–ľ–ł, —ā–ĺ–Ī—ā–ĺ ( ) Ōēcos, bababa ==‚čÖ . (2) –ó (3), –≤—Ä–į—Ö–ĺ–≤—É—é—á–ł (2), –≤–ł–Ņ–Ľ–ł–≤–į—Ē, —Č–ĺ 222222 cos zyxzyx zzyyxx bbbaaa bababa ++‚čÖ++ ++ =Ōē (3) –Į–ļ—Č–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł a —Ė b –≤–∑–į—Ē–ľ–Ĺ–ĺ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—Ė, —ā–ĺ ŌÜ = 2 ŌÄ , —ā–ĺ–ī—Ė cos ŌÜ = 0, –∑–≤—Ė–ī–ļ–ł –≤–ł–Ņ–Ľ–ł–≤–į—Ē —É–ľ–ĺ–≤–į –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ—Ā—ā—Ė : ax bx + ay by + az bz = 0. –í–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –Ę—Ä–ł –≤–Ķ–ļ—ā–ĺ—Ä–ł –Ĺ–į–∑–ł–≤–į—é—ā—Ć—Ā—Ź –≤–Ņ–ĺ—Ä—Ź–ī–ļ–ĺ–≤–į–Ĺ–ĺ—é —ā—Ä—Ė–Ļ–ļ–ĺ—é –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤, —Ź–ļ—Č–ĺ –≤–ļ–į–∑–į–Ĺ–ĺ, —Ź–ļ–ł–Ļ –∑ –Ĺ–ł—Ö –Ņ–Ķ—Ä—ą–ł–Ļ, —Ź–ļ–ł–Ļ –ī—Ä—É–≥–ł–Ļ —Ė —Ź–ļ–ł–Ļ —ā—Ä–Ķ—ā—Ė–Ļ. –†–ĺ–∑–≥–Ľ—Ź–Ĺ–Ķ–ľ–ĺ –Ņ—Ä—Ź–ľ–ĺ–ļ—É—ā–Ĺ—É —Ā–ł—Ā—ā–Ķ–ľ—É –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā. –ě–ī–ł–Ĺ–ł—á–Ĺ—Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł kji ,, , —Ź–ļ—Ė —Ā–Ņ—Ė–≤–Ņ–į–ī–į—é—ā—Ć –∑ –ī–ĺ–ī–į—ā–Ĺ–ł–ľ–ł –Ĺ–į–Ņ—Ä—Ź–ľ–į–ľ–ł –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ĺ –ĺ—Ā–Ķ–Ļ –į–Ī—Ā—Ü–ł—Ā, –ĺ—Ä–ī–ł–Ĺ–į—ā —Ė –į–Ņ–Ľ—Ė–ļ–į—ā, –Ĺ–į–∑–ł–≤–į—é—ā—Ć—Ā—Ź –ĺ—Ä—ā–į–ľ–ł. –ü–Ķ—Ä—ą–ł–ľ –≤–Ķ–ļ—ā–ĺ—Ä–ĺ–ľ –≤–≤–į–∂–į—Ē—ā—Ć—Ā—Ź –≤–Ķ–ļ—ā–ĺ—Ä i , –ī—Ä—É–≥–ł–ľ ‚ÄĒ j , –į —ā—Ä–Ķ—ā—Ė–ľ ‚ÄĒ –≤–Ķ–ļ—ā–ĺ—Ä k . –ü—Ä—Ź–ľ–ĺ–ļ—É—ā–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –Ņ—Ä–į–≤–ĺ—é (—Ä–ł—Ā. 1), —Ź–ļ—Č–ĺ –∑ –ļ—Ė–Ĺ—Ü—Ź —ā—Ä–Ķ—ā—Ć–ĺ–≥–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–į k –Ņ–ĺ–≤–ĺ—Ä–ĺ—ā –≤—Ė–ī –Ņ–Ķ—Ä—ą–ĺ–≥–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–į i –ī–ĺ –ī—Ä—É–≥–ĺ–≥–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–į j –≤—Ė–ī–Ī—É–≤–į—Ē—ā—Ć—Ā—Ź –Ņ—Ä–ĺ—ā–ł —Ä—É—Ö—É –≥–ĺ–ī–ł–Ĺ–Ĺ–ł–ļ–ĺ–≤–ĺ—ó —Ā—ā—Ä—Ė–Ľ–ļ–ł.
- 4. –†–ł—Ā. 1 –Ę—Ä–ł –Ĺ–Ķ–ļ–ĺ–ľ–Ņ–Ľ–į–Ĺ–į—Ä–Ĺ—Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł a , b —Ė c –Ĺ–į–∑–ł–≤–į—é—ā—Ć—Ā—Ź –Ņ—Ä–į–≤–ĺ—é —ā—Ä—Ė–Ļ–ļ–ĺ—é, —Ź–ļ—Č–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł a , b —Ė c –ĺ—Ä—Ė—Ē–Ĺ—ā–ĺ–≤–į–Ĺ—Ė —ā–į–ļ —Ā–į–ľ–ĺ, —Ź–ļ —Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł kji ,, . –í–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–ľ –ī–ĺ–Ī—É—ā–ļ–ĺ–ľ –≤–Ķ–ļ—ā–ĺ—Ä–į a –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä b –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź —ā–į–ļ–ł–Ļ –≤–Ķ–ļ—ā–ĺ—Ä c , —Ź–ļ–ł–Ļ: 1) –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ł–Ļ –ī–ĺ –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —Ė b ; 2) –∑ –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł a , b —É—ā–≤–ĺ—Ä—é—Ē –Ņ—Ä–į–≤—É —ā—Ä—Ė–Ļ–ļ—É; 3) –ľ–į—Ē –ī–ĺ–≤–∂–ł–Ĺ—É, —Ź–ļ–į –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź –∑–į —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é Ōēsinbac = (ŌÜ ‚ÄĒ –ļ—É—ā –ľ—Ė–∂ –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł a —Ė b ) (—Ä–ł—Ā. 2). –í–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —Ė b –Ņ–ĺ–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ ba √ó , –į–Ī–ĺ [ ]ba, . –†–ł—Ā. 2 –ó –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ī—É—ā–ļ—É –≤–ł–Ņ–Ľ–ł–≤–į—Ē, —Č–ĺ –ī–ĺ–≤–∂–ł–Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į ba √ó —á–ł—Ā–Ķ–Ľ—Ć–Ĺ–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –Ņ–Ľ–ĺ—Č—Ė –Ņ–į—Ä–į–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–į, –Ņ–ĺ–Ī—É–ī–ĺ–≤–į–Ĺ–ĺ–≥–ĺ –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į—Ö a —Ė b —Ź–ļ –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–į—Ö, —ā–ĺ–Ī—ā–ĺ [ ] OABCSba =, (4) –ě—Ā–Ĺ–ĺ–≤–Ĺ—Ė –≤–Ľ–į—Ā—ā–ł–≤–ĺ—Ā—ā—Ė –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ī—É—ā–ļ—É: ‚ÄĘ –Ņ—Ä–ł –Ņ–Ķ—Ä–Ķ—Ā—ā–į–≤–Ľ—Ź–Ĺ–Ĺ—Ė —Ā–Ņ—Ė–≤–ľ–Ĺ–ĺ–∂–Ĺ–ł–ļ—Ė–≤ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –∑–ľ—Ė–Ĺ—é—Ē —Ā–≤—Ė–Ļ –∑–Ĺ–į–ļ, —ā–ĺ–Ī—ā–ĺ ( )abba √ó‚ąí=√ó (–≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –Ĺ–Ķ –ľ–į—Ē –ļ–ĺ–ľ—É—ā–į—ā–ł–≤–Ĺ–ĺ—ó –≤–Ľ–į—Ā—ā–ł–≤–ĺ—Ā—ā—Ė); ‚ÄĘ –ľ–į—Ē —Ā–Ņ–ĺ–Ľ—É—á–Ĺ—É –≤–Ľ–į—Ā—ā–ł–≤—Ė—Ā—ā—Ć —Č–ĺ–ī–ĺ —á–ł—Ā–Ľ–ĺ–≤–ĺ–≥–ĺ –ľ–Ĺ–ĺ–∂–Ĺ–ł–ļ–į, —ā–ĺ–Ī—ā–ĺ ( ) ( ) ( )bababa őĽőĽőĽ √ó=√ó=√ó ; ‚ÄĘ –ľ–į—Ē –ī–ł—Ā—ā—Ä–ł–Ī—É—ā–ł–≤–Ĺ—É –≤–Ľ–į—Ā—ā–ł–≤—Ė—Ā—ā—Ć –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ľ–Ĺ–ĺ–∂–Ĺ–ł–ļ–į –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ —Ā—É–ľ–ł –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤, —ā–ĺ–Ī—ā–ĺ ( ) cbcacba √ó+√ó=√ó+ ; ‚ÄĘ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ ba √ó –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –Ĺ—É–Ľ—é, —Ź–ļ—Č–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł a —Ė b –ļ–ĺ–Ľ—Ė–Ĺ–Ķ–į—Ä–Ĺ—Ė –į–Ī–ĺ –Ņ—Ä–ł–Ĺ–į–Ļ–ľ–Ĺ—Ė –ĺ–ī–ł–Ĺ –∑ –Ĺ–ł—Ö —Ē –Ĺ—É–Ľ—Ć–ĺ–≤–ł–ľ. –Ě–į –Ņ—Ė–ī—Ā—ā–į–≤—Ė –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ī—É—ā–ļ—É –Ĺ–į–≤–Ķ–ī–Ķ–ľ–ĺ —ā–į–Ī–Ľ–ł—Ü—é –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł—Ö –ī–ĺ–Ī—É—ā–ļ—Ė–≤ –ĺ—Ä—ā—Ė–≤ kji ,, : –Ě–Ķ—Ö–į–Ļ –ī–į–Ĺ–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł );;( zyx aaaa —Ė );;( zyx bbbb , —ā–ĺ–ī—Ė, –≤—Ä–į—Ö–ĺ–≤—É—é—á–ł –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –ĺ—Ä—ā—Ė–≤ kji ,, , –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –ī–į–Ĺ–ł—Ö –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —Ė b –ľ–ĺ–∂–Ĺ–į –Ņ–ĺ–ī–į—ā–ł —É –≤–ł–≥–Ľ—Ź–ī—Ė –≤–ł–∑–Ĺ–į—á–Ĺ–ł–ļ–į
- 5. –ģ.–ú–į—Ä—á—É–ļ –ö—É—Ä—Ā –Ľ–Ķ–ļ—Ü—Ė–Ļ –∑ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł (5) –į–Ī–ĺ —É –≤–ł–≥–Ľ—Ź–ī—Ė —Ä–ĺ–∑–ļ–Ľ–į–ī—É: (6) –ú—Ė—ą–į–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –ú—Ė—ą–į–Ĺ–ł–ľ –ī–ĺ–Ī—É—ā–ļ–ĺ–ľ —É–Ņ–ĺ—Ä—Ź–ī–ļ–ĺ–≤–į–Ĺ–ĺ—ó —ā—Ä—Ė–Ļ–ļ–ł –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a , b —Ė c –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź —á–ł—Ā–Ľ–ĺ, —Ź–ļ–Ķ –ĺ–ī–Ķ—Ä–∂—É—é—ā—Ć –≤–Ĺ–į—Ā–Ľ—Ė–ī–ĺ–ļ —Ā–ļ–į–Ľ—Ź—Ä–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ī—É—ā–ļ—É –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ ba √ó —ā–į c . –ú—Ė—ą–į–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –Ņ–ĺ–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ ( ba √ó ) c , –į–Ī–ĺ ( ba √ó , c ). –Į–ļ—Č–ĺ –∑–į–ī–į–Ĺ—Ė —ā—Ä–ł –Ĺ–Ķ–ļ–ĺ–ľ–Ņ–Ľ–į–Ĺ–į—Ä–Ĺ—Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł a (ax; ay; az), b (bx;bv;bz) —Ė c (cx;cy;cz), —ā–ĺ –ľ—Ė—ą–į–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –ľ–ĺ–∂–Ĺ–į –Ņ–ĺ–ī–į—ā–ł –≤–ł–∑–Ĺ–į—á–Ĺ–ł–ļ–ĺ–ľ (7) –ź–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –ľ—Ė—ą–į–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ī—É—ā–ļ—É —ā—Ä—Ć–ĺ—Ö –Ĺ–Ķ –ļ–ĺ–ľ–Ņ–Ľ–į–Ĺ–į—Ä–Ĺ–ł—Ö –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –ĺ–Ī‚Äô—Ē–ľ—É –Ņ–į—Ä–į–Ľ–Ķ–Ľ–Ķ–Ņ—Ė–Ņ–Ķ–ī–į, –Ņ–ĺ–Ī—É–ī–ĺ–≤–į–Ĺ–ĺ–≥–ĺ –Ĺ–į —Ü–ł—Ö –≤–Ķ–ļ—ā–ĺ—Ä–į—Ö —Ź–ļ –Ĺ–į —Ä–Ķ–Ī—Ä–į—Ö (—Ä–ł—Ā. 3). –†–ł—Ā. 3 –ź –ĺ–Ī‚Äô—Ē–ľ –Ņ—Ė—Ä–į–ľ—Ė–ī–ł, –Ņ–ĺ–Ī—É–ī–ĺ–≤–į–Ĺ–ĺ—ó –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į—Ö a , b —Ė c , –∑–Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –∑–į —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é (8) –í–Ķ–ļ—ā–ĺ—Ä–ł a , b —Ė c –Ī—É–ī—É—ā—Ć –ļ–ĺ–ľ–Ņ–Ľ–į–Ĺ–į—Ä–Ĺ–ł–ľ–ł —ā–ĺ–ī—Ė —Ė —ā—Ė–Ľ—Ć–ļ–ł —ā–ĺ–ī—Ė, –ļ–ĺ–Ľ–ł (9) –ü—Ä–ł–ļ–Ľ–į–ī. –ó–Ĺ–į–Ļ—ā–ł –ĺ–Ī‚Äô—Ē–ľ –Ņ—Ė—Ä–į–ľ—Ė–ī–ł –∑ –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł: A(5; 1; - 4), B(1; 2; -1), –°(3; 3; - 4) —Ė D(2;2;2) . –† –ĺ –∑ –≤ ‚Äô —Ź –∑ –į –Ĺ –Ĺ —Ź –†–ĺ–∑–≥–Ľ—Ź–Ĺ–Ķ–ľ–ĺ —ā—Ä–ł –≤–Ķ–ļ—ā–ĺ—Ä–ł a = –ź–í , b = –ź–° —Ė c = AD . –ó–į –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ł–ľ–ł —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ–ł –∑–Ĺ–į—Ö–ĺ–ī–ł–ľ–ĺ
- 6. –į—Ö = -4; –į—É=1; –įz= 3; b—Ö=-2; by =2; bz= 0; —Ā—Ö = -3; —Āy =1; —Āz = 6. –ě–Ī‚Äô—Ē–ľ —ą—É–ļ–į–Ĺ–ĺ—ó –Ņ—Ė—Ä–į–ľ—Ė–ī–ł —ą—É–ļ–į—Ē–ľ–ĺ –∑–į —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é: –Ē–ě–í–Ė–ė–Ě–ź –í–ē–ö–Ę–ě–†–ź, –ö–£–Ę –ú–Ü–Ė –í–ē–ö–Ę–ě–†–ź–ú–ė, –í–Ü–Ē–°–Ę–ź–Ě–¨ –ú–Ü–Ė –Ē–í–ě–ú–ź –Ę–ě–ß–ö–ź–ú–ė –Ē–ĺ–≤–∂–ł–Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į –į (–į1; –į2; –į3) –ĺ–Ī—á–ł—Ā–Ľ—é—Ē—ā—Ć—Ā—Ź –∑–į —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é: 2 3 2 2 2 1 aaaa ++= –ö—É—ā–ĺ–ľ –ľ—Ė–∂ –Ĺ–Ķ–Ĺ—É–Ľ—Ć–ĺ–≤–ł–ľ–ł –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł –ź–í —Ė –ź–° –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –ļ—É—ā ‚ą† –í–ź–°. –ö—É—ā–ĺ–ľ –ľ—Ė–∂ –Ī—É–ī—Ć-—Ź–ļ–ł–ľ–ł –Ĺ–Ķ–Ĺ—É–Ľ—Ć–ĺ–≤–ł–ľ–ł –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł –į —Ė b –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –ļ—É—ā –ľ—Ė–∂ –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł, —Č–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—é—ā—Ć –ī–į–Ĺ–ł–ľ —Ė –ľ–į—é—ā—Ć —Ā–Ņ—Ė–Ľ—Ć–Ĺ–ł–Ļ –Ņ–ĺ—á–į—ā–ĺ–ļ. –ö—É—ā –ľ—Ė–∂ –ī–≤–ĺ–ľ–į –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł –ľ–ĺ–∂–Ĺ–į –ĺ–Ī—á–ł—Ā–Ľ–ł—ā–ł —á–Ķ—Ä–Ķ–∑ —Ā–ļ–į–Ľ—Ź—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ —Ü–ł—Ö –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤: ba ab ‚čÖ =Ōēcos –Į–ļ—Č–ĺ —Ā–ļ–į–Ľ—Ź—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –Ĺ–Ķ–Ĺ—É–Ľ—Ć–ĺ–≤–ł—Ö –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –Ĺ—É–Ľ—é, —ā–ĺ —Ü—Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—Ė. –†—Ė–∑–Ĺ–ĺ–Ļ–ľ–Ķ–Ĺ–Ĺ—Ė –ĺ—Ä—ā–ł ‚Äď –≤–∑–į—Ē–ľ–Ĺ–ĺ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—Ė. –°–ļ–į–Ľ—Ź—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ —Ä—Ė–∑–Ĺ–ĺ–Ļ–ľ–Ķ–Ĺ–Ĺ–ł—Ö –ĺ—Ä—ā—Ė–≤ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –Ĺ—É–Ľ—é. –í—Ė–ī—Ā—ā–į–Ĺ—Ć –ľ—Ė–∂ —ā–ĺ—á–ļ–į–ľ–ł A1(x1; y1; z1) —Ė A2(x2; y2; z2) (–ī–ĺ–≤–∂–ł–Ĺ–į –≤—Ė–ī—Ä—Ė–∑–ļ–į –ź1–ź2) –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź –∑–į —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é: ( ) ( ) ( )2 12 2 12 2 1221 zzyyxxAA ‚ąí+‚ąí+‚ąí= –Ě–Ķ—Ö–į–Ļ —ā–ĺ—á–ļ–į –ě ‚Äď —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į –≤—Ė–ī—Ä—Ė–∑–ļ–į –ź1–ź2. A1(x1; y1; z1), A2(x2; y2; z2) —Ė –ě(x; y; z) –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł —ā–ĺ—á–ļ–ł –ě –≤–ł–∑–Ĺ–į—á–į—é—ā—Ć—Ā—Ź –∑–į —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ–ł: 2 21 xx x + = 2 21 yy y + = 2 21 zz z + = –†–ĺ–∑–ļ–Ľ–į–ī–į–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä–į –Ĺ–į —Ā–ļ–Ľ–į–ī–ĺ–≤—Ė (–Ņ—Ä–ĺ–ī–ĺ–≤–∂–Ķ–Ĺ–Ĺ—Ź) –ě—Ā–ļ—Ė–Ľ—Ć–ļ–ł –ĺ—Ä—ā–ł –≤—Ė–ī–ľ—Ė–Ĺ–Ĺ—Ė –≤—Ė–ī –Ĺ—É–Ľ—Ź —Ė –Ĺ–Ķ –ļ–ĺ–Ľ—Ė–Ĺ–Ķ–į—Ä–Ĺ—Ė, —ā–ĺ –Ī—É–ī—Ć-—Ź–ļ–ł–Ļ –≤–Ķ–ļ—ā–ĺ—Ä –į (–į1; –į2; –į3) –ľ–ĺ–∂–Ĺ–į –∑–į–Ņ–ł—Ā–į—ā–ł —É –≤–ł–≥–Ľ—Ź–ī—Ė: 321 eeea őŬĶőĽ ++= (*) –í–ł–∑–Ĺ–į—á–ł–ľ–ĺ őĽ, ¬Ķ, őĹ. –ü–ĺ–ľ–Ĺ–ĺ–∂–ł–ľ–ĺ —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź (*) –Ĺ–į 1–Ķ . –í—Ä–į—Ö—É–≤–į–≤—ą–ł, —Č–ĺ —Ā–ļ–į–Ľ—Ź—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –ĺ–ī–Ĺ–ĺ–Ļ–ľ–Ķ–Ĺ–Ĺ–ł—Ö –ĺ—Ä—ā—Ė–≤ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē 1, –ĺ–ī–Ķ—Ä–∂–ł–ľ–ĺ: ( ) ( ) 11321 0;0;1;; aeaaaa =‚čÖ , őĽőĽ =‚čÖ 11 ee , 012 =‚čÖee¬Ķ , 013 =‚čÖeeőĹ . –ě—ā–∂–Ķ, 1aőĽ = . –ź–Ĺ–į–Ľ–ĺ–≥—Ė—á–Ĺ–ĺ, —Ź–ļ—Č–ĺ —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź (*) –Ņ–ĺ–ľ–Ĺ–ĺ–∂–ł—ā–ł –Ĺ–į 2–Ķ , —ā–ĺ –ĺ–ī–Ķ—Ä–∂–ł–ľ–ĺ: ¬Ķ = –į2. –Ü —Ź–ļ—Č–ĺ —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź (*) –Ņ–ĺ–ľ–Ĺ–ĺ–∂–ł—ā–ł –Ĺ–į 3–Ķ , —ā–ĺ –ĺ–ī–Ķ—Ä–∂–ł–ľ–ĺ: őĹ = –į3. –í —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā—Ė –ĺ–ī–Ķ—Ä–∂–ł–ľ–ĺ —Ä–ĺ–∑–ļ–Ľ–į–ī –≤–Ķ–ļ—ā–ĺ—Ä–į –Ĺ–į —Ā–ļ–Ľ–į–ī–ĺ–≤—Ė: 332211 –Ķ–į–Ķ–į–Ķ–į–į ‚čÖ+‚čÖ+‚čÖ= –į–Ī–ĺ k–įj–įi–į–į ‚čÖ+‚čÖ+‚čÖ= 321


![–†–ł—Ā. 1
–Ę—Ä–ł –Ĺ–Ķ–ļ–ĺ–ľ–Ņ–Ľ–į–Ĺ–į—Ä–Ĺ—Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł a , b —Ė c –Ĺ–į–∑–ł–≤–į—é—ā—Ć—Ā—Ź –Ņ—Ä–į–≤–ĺ—é —ā—Ä—Ė–Ļ–ļ–ĺ—é, —Ź–ļ—Č–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł a , b —Ė c
–ĺ—Ä—Ė—Ē–Ĺ—ā–ĺ–≤–į–Ĺ—Ė —ā–į–ļ —Ā–į–ľ–ĺ, —Ź–ļ —Ė –≤–Ķ–ļ—ā–ĺ—Ä–ł kji ,, .
–í–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–ľ –ī–ĺ–Ī—É—ā–ļ–ĺ–ľ –≤–Ķ–ļ—ā–ĺ—Ä–į a –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä b –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź —ā–į–ļ–ł–Ļ –≤–Ķ–ļ—ā–ĺ—Ä c , —Ź–ļ–ł–Ļ:
1) –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ł–Ļ –ī–ĺ –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —Ė b ;
2) –∑ –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł a , b —É—ā–≤–ĺ—Ä—é—Ē –Ņ—Ä–į–≤—É —ā—Ä—Ė–Ļ–ļ—É;
3) –ľ–į—Ē –ī–ĺ–≤–∂–ł–Ĺ—É, —Ź–ļ–į –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź –∑–į —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é Ōēsinbac = (ŌÜ ‚ÄĒ –ļ—É—ā –ľ—Ė–∂ –≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł a —Ė b )
(—Ä–ł—Ā. 2).
–í–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —Ė b –Ņ–ĺ–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ ba √ó , –į–Ī–ĺ [ ]ba, .
–†–ł—Ā. 2
–ó –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ī—É—ā–ļ—É –≤–ł–Ņ–Ľ–ł–≤–į—Ē, —Č–ĺ –ī–ĺ–≤–∂–ł–Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į ba √ó —á–ł—Ā–Ķ–Ľ—Ć–Ĺ–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –Ņ–Ľ–ĺ—Č—Ė
–Ņ–į—Ä–į–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–į, –Ņ–ĺ–Ī—É–ī–ĺ–≤–į–Ĺ–ĺ–≥–ĺ –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į—Ö a —Ė b —Ź–ļ –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–į—Ö, —ā–ĺ–Ī—ā–ĺ
[ ] OABCSba =, (4)
–ě—Ā–Ĺ–ĺ–≤–Ĺ—Ė –≤–Ľ–į—Ā—ā–ł–≤–ĺ—Ā—ā—Ė –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ī—É—ā–ļ—É:
‚ÄĘ –Ņ—Ä–ł –Ņ–Ķ—Ä–Ķ—Ā—ā–į–≤–Ľ—Ź–Ĺ–Ĺ—Ė —Ā–Ņ—Ė–≤–ľ–Ĺ–ĺ–∂–Ĺ–ł–ļ—Ė–≤ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –∑–ľ—Ė–Ĺ—é—Ē —Ā–≤—Ė–Ļ –∑–Ĺ–į–ļ, —ā–ĺ–Ī—ā–ĺ
( )abba √ó‚ąí=√ó
(–≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –Ĺ–Ķ –ľ–į—Ē –ļ–ĺ–ľ—É—ā–į—ā–ł–≤–Ĺ–ĺ—ó –≤–Ľ–į—Ā—ā–ł–≤–ĺ—Ā—ā—Ė);
‚ÄĘ –ľ–į—Ē —Ā–Ņ–ĺ–Ľ—É—á–Ĺ—É –≤–Ľ–į—Ā—ā–ł–≤—Ė—Ā—ā—Ć —Č–ĺ–ī–ĺ —á–ł—Ā–Ľ–ĺ–≤–ĺ–≥–ĺ –ľ–Ĺ–ĺ–∂–Ĺ–ł–ļ–į, —ā–ĺ–Ī—ā–ĺ
( ) ( ) ( )bababa őĽőĽőĽ √ó=√ó=√ó ;
‚ÄĘ –ľ–į—Ē –ī–ł—Ā—ā—Ä–ł–Ī—É—ā–ł–≤–Ĺ—É –≤–Ľ–į—Ā—ā–ł–≤—Ė—Ā—ā—Ć –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ľ–Ĺ–ĺ–∂–Ĺ–ł–ļ–į –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ —Ā—É–ľ–ł –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤, —ā–ĺ–Ī—ā–ĺ
( ) cbcacba √ó+√ó=√ó+ ;
‚ÄĘ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ ba √ó –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –Ĺ—É–Ľ—é, —Ź–ļ—Č–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł a —Ė b –ļ–ĺ–Ľ—Ė–Ĺ–Ķ–į—Ä–Ĺ—Ė –į–Ī–ĺ –Ņ—Ä–ł–Ĺ–į–Ļ–ľ–Ĺ—Ė
–ĺ–ī–ł–Ĺ –∑ –Ĺ–ł—Ö —Ē –Ĺ—É–Ľ—Ć–ĺ–≤–ł–ľ.
–Ě–į –Ņ—Ė–ī—Ā—ā–į–≤—Ė –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ī—É—ā–ļ—É –Ĺ–į–≤–Ķ–ī–Ķ–ľ–ĺ —ā–į–Ī–Ľ–ł—Ü—é –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł—Ö –ī–ĺ–Ī—É—ā–ļ—Ė–≤ –ĺ—Ä—ā—Ė–≤ kji ,, :
–Ě–Ķ—Ö–į–Ļ –ī–į–Ĺ–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–ł );;( zyx aaaa —Ė );;( zyx bbbb , —ā–ĺ–ī—Ė, –≤—Ä–į—Ö–ĺ–≤—É—é—á–ł –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –ĺ—Ä—ā—Ė–≤
kji ,, , –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ł–Ļ –ī–ĺ–Ī—É—ā–ĺ–ļ –ī–į–Ĺ–ł—Ö –≤–Ķ–ļ—ā–ĺ—Ä—Ė–≤ a —Ė b –ľ–ĺ–∂–Ĺ–į –Ņ–ĺ–ī–į—ā–ł —É –≤–ł–≥–Ľ—Ź–ī—Ė –≤–ł–∑–Ĺ–į—á–Ĺ–ł–ļ–į](https://image.slidesharecdn.com/random-160728192536/85/-4-320.jpg)
























































































