СӮРёРјРҫРј 2016 2_5
- 1. РәР°РҪРҙ. РҝРөРҙ. РҪР°СғРә, РҙРҫСҶ.РәР°РҪРҙ. РҝРөРҙ. РҪР°СғРә, РҙРҫСҶ. Р’СҸСҮРөСҒлав ЕвгРөРҪСҢРөРІРёСҮ РҹСӢСҖРәРҫРІР’СҸСҮРөСҒлав ЕвгРөРҪСҢРөРІРёСҮ РҹСӢСҖРәРҫРІ pyrkovve@yandex.rupyrkovve@yandex.ru РӣРөРәСҶРёСҸРӣРөРәСҶРёСҸ 55.. РңРөСӮРҫРҙРёРәР° РёР·СғСҮРөРҪРёСҸРңРөСӮРҫРҙРёРәР° РёР·СғСҮРөРҪРёСҸ СҮРёСҒР»РҫРІСӢС… СҒРёСҒСӮРөРј:СҮРёСҒР»РҫРІСӢС… СҒРёСҒСӮРөРј: РҪР°СӮСғСҖалСҢРҪСӢРө СҮРёСҒлаРҪР°СӮСғСҖалСҢРҪСӢРө СҮРёСҒла
- 2. РҹлаРҪРҹлаРҪ 1. РҹРҫРҪСҸСӮРёРө СҮРёСҒла РІ РјР°СӮРөРјР°СӮРёРәРө 2. РһСҒРҪРҫРІРҪСӢРө СҚСӮР°РҝСӢ СҖазвиСӮРёСҸ РҝРҫРҪСҸСӮРёСҸ СҮРёСҒла 3. Р Р°СҒСҲРёСҖРөРҪРёСҸ РҝРҫРҪСҸСӮРёСҸ СҮРёСҒла 4. РҰРөли РёР·СғСҮРөРҪРёСҸ лиРҪРёРё СҮРёСҒРөР» 5. РӯСӮР°РҝСӢ РёР·СғСҮРөРҪРёСҸ лиРҪРёРё СҮРёСҒРөР» 6. РһРұСүР°СҸ СҒС…РөРјР° РёР·СғСҮРөРҪРёСҸ СҮРёСҒРөР»
- 3. РҹРҫРҪСҸСӮРёРө СҮРёСҒла РІ РјР°СӮРөРјР°СӮРёРәРөРҹРҫРҪСҸСӮРёРө СҮРёСҒла РІ РјР°СӮРөРјР°СӮРёРәРө ЧиСҒР»РҫЧиСҒР»Рҫ вҖ“ СҒСӮРөСҖР¶РҪРөРІРҫРө РҝРҫРҪСҸСӮРёРө СҲРәРҫР»СҢРҪРҫРіРҫ РәСғСҖСҒР°, С„СғРҪРҙамРөРҪСӮ, РҪР° РәРҫСӮРҫСҖРҫРј СҒСӮСҖРҫРёСӮСҒСҸ РёР·СғСҮРөРҪРёРө С„СғРҪРәСҶРёР№, СӮРҫР¶РҙРөСҒСӮРІРөРҪРҪСӢС… РҝСҖРөРҫРұСҖазРҫРІР°РҪРёР№, СғСҖавРҪРөРҪРёР№ Рё СӮ.Рҝ.; РҝРҫРҪСҸСӮРёРө СҮРёСҒла РҫСӮРҪРҫСҒРёСӮСҒСҸ Рә РҫСҒРҪРҫРІРҪСӢРј РҝРҫРҪСҸСӮРёСҸРј РјР°СӮРөРјР°СӮРёРәРё ЧиСҒла РІРҫР·РҪРёРәли РёР· РҝРҫСӮСҖРөРұРҪРҫСҒСӮРөР№ СҒСҮРөСӮР°РҝРҫСӮСҖРөРұРҪРҫСҒСӮРөР№ СҒСҮРөСӮР° Рё РёР·РјРөСҖРөРҪРёСҸРёР·РјРөСҖРөРҪРёСҸ Рё РҝСҖРөСӮРөСҖРҝРөли РҙлиСӮРөР»СҢРҪСӢР№ РҝСғСӮСҢ РёСҒСӮРҫСҖРёСҮРөСҒРәРҫРіРҫ СҖазвиСӮРёСҸ, РІ С…РҫРҙРө РәРҫСӮРҫСҖРҫРіРҫ РјРөРҪСҸлиСҒСҢ Р·Р°РҝР°СҒ СҮРёСҒРөР», РёС… РҪазваРҪРёСҸ РёР·Р°РҝР°СҒ СҮРёСҒРөР», РёС… РҪазваРҪРёСҸ Рё РҫРұРҫР·РҪР°СҮРөРҪРёСҸРҫРұРҫР·РҪР°СҮРөРҪРёСҸ.
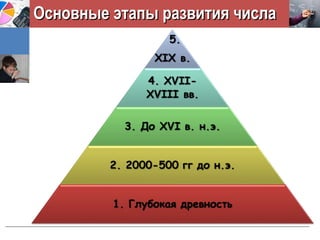
- 4. РһСҒРҪРҫРІРҪСӢРө СҚСӮР°РҝСӢ СҖазвиСӮРёСҸ СҮРёСҒлаРһСҒРҪРҫРІРҪСӢРө СҚСӮР°РҝСӢ СҖазвиСӮРёСҸ СҮРёСҒла
- 6. Р Р°СҒСҲРёСҖРөРҪРёРө РҝРҫРҪСҸСӮРёСҸ СҮРёСҒлаРаСҒСҲРёСҖРөРҪРёРө РҝРҫРҪСҸСӮРёСҸ СҮРёСҒла РҹСғСҒСӮСҢ РјРҪРҫР¶РөСҒСӮРІРҫ РҗРҗ СҖР°СҒСҲРёСҖСҸРөСӮСҒСҸ РҙРҫ РјРҪРҫР¶РөСҒСӮРІР° Р’Р’. РўРҫРіРҙР° РҙРҫлжРҪСӢ РІСӢРҝРҫР»РҪСҸСӮСҢСҒСҸ СғСҒР»РҫРІРёСҸ: 1)1)РҗРҗ РҙРҫлжРҪРҫ РұСӢСӮСҢ РҝРҫРҙРјРҪРҫР¶РөСҒСӮРІРҫРј Р’Р’. 2)Р’СҒРө РҫРҝРөСҖР°СҶРёРё Рё РҫСӮРҪРҫСҲРөРҪРёСҸ РҪР°Рҙ СҚР»РөРјРөРҪСӮами РёР· РјРҪРҫР¶РөСҒСӮРІР° РҗРҗ СӮРө Р¶Рө, СҮСӮРҫ Рё РҙР»СҸ СҚР»РөРјРөРҪСӮРҫРІ РёР· РјРҪРҫР¶РөСҒСӮРІР° Р’Р’, РҪРҫ РёС… СҒРјСӢСҒР» РҙР»СҸ СҚР»РөРјРөРҪСӮРҫРІ РҗРҗ, СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјСӢС… РәР°Рә СҚР»РөРјРөРҪСӮСӢ Р’Р’, РҙРҫлжРөРҪ СҒРҫРІРҝР°РҙР°СӮСҢ СҒ СӮРөРј, РәР°РәРҫР№ РҫРҪРё РёРјРөли РҙРҫ СҖР°СҒСҲРёСҖРөРҪРёСҸ РІ РјРҪРҫР¶РөСҒСӮРІРө РҗРҗ. 3)Р’ РјРҪРҫР¶РөСҒСӮРІРө Р’Р’ РҙРҫлжРҪР° РұСӢСӮСҢ РІСӢРҝРҫР»РҪРёРјР° РҫРҝРөСҖР°СҶРёСҸ, РәРҫСӮРҫСҖР°СҸ РІ РјРҪРҫР¶РөСҒСӮРІРө РҗРҗ РұСӢла РҪРөРІСӢРҝРҫР»РҪРёРјР° или РҪРө РІСҒРөРіРҙР° РІСӢРҝРҫР»РҪРёРјР°. 4)Р Р°СҒСҲРёСҖРөРҪРёРө Р’Р’ РҙРҫлжРҪРҫ РұСӢСӮСҢ «миРҪималСҢРҪСӢРјВ» СҒСҖРөРҙРё РІСҒРөС… РІРҫР·РјРҫР¶РҪСӢС… СҖР°СҒСҲРёСҖРөРҪРёР№ РјРҪРҫР¶РөСҒСӮРІР° РҗРҗ, СғРҙРҫРІР»РөСӮРІРҫСҖСҸСҺСүРёС… СғСҒР»РҫРІРёСҸРј 1-3, СӮ.Рө. СӮР°РәРёРј, СҮСӮРҫРұСӢ РҪРө СҒСғСүРөСҒСӮРІРҫвалРҫ РҪРёРәР°РәРҫРіРҫ РҝРҫРҙРјРҪРҫР¶РөСҒСӮРІР° Р’Р’, СҒРҫРҙРөСҖжаСүРөРіРҫ РҗРҗ Рё СғРҙРҫРІР»РөСӮРІРҫСҖСҸСҺСүРөРіРҫ СӮРөРј Р¶Рө СғСҒР»РҫРІРёСҸРј.
- 7. РҹСғСӮРё СҖР°СҒСҲРёСҖРөРҪРёСҸ РҝРҫРҪСҸСӮРёСҸ СҮРёСҒлаРҹСғСӮРё СҖР°СҒСҲРёСҖРөРҪРёСҸ РҝРҫРҪСҸСӮРёСҸ СҮРёСҒла РӣРһР“РҳЧЕСРҡРҗРҜ РЎРҘР•РңРҗ Р РҗРЎРЁРҳР Р•РқРҳРҜ РҹРһРқРҜРўРҳРҜ Р§РҳРЎРӣРҗРӣРһР“РҳЧЕСРҡРҗРҜ РЎРҘР•РңРҗ Р РҗРЎРЁРҳР Р•РқРҳРҜ РҹРһРқРҜРўРҳРҜ Р§РҳРЎРӣРҗ NN вҶ’вҶ’ ZZ вҶ’вҶ’ QQ вҶ’вҶ’ RR вҶ’вҶ’ CC РҳРЎРўРһР РҳЧЕСРҡРҗРҜ РЎРҘР•РңРҗ Р РҗРЎРЁРҳР Р•РқРҳРҜ РҹРһРқРҜРўРҳРҜ Р§РҳРЎРӣРҗРҳРЎРўРһР РҳЧЕСРҡРҗРҜ РЎРҘР•РңРҗ Р РҗРЎРЁРҳР Р•РқРҳРҜ РҹРһРқРҜРўРҳРҜ Р§РҳРЎРӣРҗ NN00 вҶ’вҶ’ QQ++ вҶ’вҶ’ QQ вҶ’вҶ’ RR вҶ’вҶ’ CC Р’ СғСҒСӮР°РҪРҫРІРёРІСҲРөР№СҒСҸ СҲРәРҫР»СҢРҪРҫР№ РҝСҖР°РәСӮРёРәРө РёСҒРҝРҫР»СҢР·СғРөСӮСҒСҸ РёСҒСӮРҫСҖРёСҮРөСҒРәР°СҸ РҝРҫСҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫСҒСӮСҢ СҖазвиСӮРёСҸ РҝРҫРҪСҸСӮРёСҸ СҮРёСҒла: РҙСҖРҫРұРё РёР·СғСҮР°СҺСӮСҒСҸ СҖР°РҪСҢСҲРө РҫСӮСҖРёСҶР°СӮРөР»СҢРҪСӢС… СҮРёСҒРөР».
- 8. РҰРөли РёР·СғСҮРөРҪРёСҸ лиРҪРёРё СҮРёСҒРөР»РҰРөли РёР·СғСҮРөРҪРёСҸ лиРҪРёРё СҮРёСҒРөР»
- 9. РӯСӮР°РҝСӢ РёР·СғСҮРөРҪРёСҸ лиРҪРёРё СҮРёСҒРөР»РӯСӮР°РҝСӢ РёР·СғСҮРөРҪРёСҸ лиРҪРёРё СҮРёСҒРөР»
- 10. РһРұСүР°СҸ СҒС…РөРјР° РёР·СғСҮРөРҪРёСҸ СҮРёСҒРөР»РһРұСүР°СҸ СҒС…РөРјР° РёР·СғСҮРөРҪРёСҸ СҮРёСҒРөР»
- 11. РһРұСүР°СҸ СҒС…РөРјР° РёР·СғСҮРөРҪРёСҸ СҮРёСҒРөР»РһРұСүР°СҸ СҒС…РөРјР° РёР·СғСҮРөРҪРёСҸ СҮРёСҒРөР»
Editor's Notes
- #3: РӣРёСҲСҢ РҝРҫСҒСӮРөРҝРөРҪРҪРҫ СҮРөР»РҫРІРөСҮРөСҒСӮРІРҫ РҙРҫСҒСӮРёРіР»Рҫ СҒРҫРІСҖРөРјРөРҪРҪРҫРіРҫ РҝРҫРҪСҸСӮРёСҸ Рҫ СҮРёСҒлах Рё СҒРҫРІСҖРөРјРөРҪРҪРҫР№ СҒРёСҒСӮРөРјСӢ РҫРұРҫР·РҪР°СҮРөРҪРёСҸ СҮРёСҒРөР». Р Р°СҒСҒРјРҫСӮСҖРёРј РҫСҒРҪРҫРІРҪСӢРө СҚСӮР°РҝСӢ СҖазвиСӮРёСҸ СҮРёСҒла:
- #4: РӣРёСҲСҢ РҝРҫСҒСӮРөРҝРөРҪРҪРҫ СҮРөР»РҫРІРөСҮРөСҒСӮРІРҫ РҙРҫСҒСӮРёРіР»Рҫ СҒРҫРІСҖРөРјРөРҪРҪРҫРіРҫ РҝРҫРҪСҸСӮРёСҸ Рҫ СҮРёСҒлах Рё СҒРҫРІСҖРөРјРөРҪРҪРҫР№ СҒРёСҒСӮРөРјСӢ РҫРұРҫР·РҪР°СҮРөРҪРёСҸ СҮРёСҒРөР». Р Р°СҒСҒРјРҫСӮСҖРёРј РҫСҒРҪРҫРІРҪСӢРө СҚСӮР°РҝСӢ СҖазвиСӮРёСҸ СҮРёСҒла:
- #5: 1 СҚСӮР°Рҝ: Р—Р°СҖРҫР¶РҙРөРҪРёРө РҝРҫРҪСҸСӮРёСҸ N-СҮРёСҒла РІ СҒРІСҸР·Рё СҒ РҝСҖРёРјРёСӮРёРІРҪСӢРј СҒСҮРөСӮРҫРј РәРҫРҪРәСҖРөСӮРҪСӢС… РҝСҖРөРҙРјРөСӮРҫРІ | РҝСғСӮРөРј СҒРҫРҝРҫСҒСӮавлРөРҪРёСҸ СҒ РҝалСҢСҶами СҖСғРә Рё РҪРҫРі СҮРөР»РҫРІРөРәР° или РҪРөСҒРәРҫР»СҢРәРёС… Р»СҺРҙРөР№, РөСҒли СҮРёСҒР»Рҫ РҝСҖРөРҙРјРөСӮРҫРІ РҝСҖРөРІСӢСҲалРҫ 20. [РЈ РҪРөРәРҫСӮРҫСҖСӢС… РҪР°СҖРҫРҙРҫРІ РҙР»СҸ 5 РҪазваРҪРёРө В«СҖСғРәа», РҙР»СҸ 20 РҪазваРҪРёРө «вРөСҒСҢ СҮРөР»РҫРІРөРәВ»]. РҹРөСҖРІРҫРҪР°СҮалСҢРҪРҫ СҮРёСҒла РұСӢли РёРјРөРҪРҫРІР°РҪРҪСӢРјРё | СӮ.Рө. РҫРҙРҪРё СҮРёСҒла РёСҒРҝРҫР»СҢР·РҫвалиСҒСҢ РҙР»СҸ СҒСҮРөСӮР° Р»СҺРҙРөР№, РҙСҖСғРіРёРө вҖ“ РҙР»СҸ СҒСҮРөСӮР° Р»РҫРҙРҫРә, РәРҫРәРҫСҒРҫРІСӢС… РҫСҖРөС…РҫРІ Рё СӮ.Рҙ.. РЎРІСҸР·СҢ РҝРөСҖРІСӢС… РҙРөСҒСҸСӮРё РҪР°СӮСғСҖалСҢРҪСӢС… СҮРёСҒРөР» СҒ РҝалСҢСҶами СҖСғРә СҮРөР»РҫРІРөРәР° СҸРІР»СҸРөСӮСҒСҸ РҪРөРҫСҒРҝРҫСҖРёРјСӢРј фаРәСӮРҫРј: РўРөСҖРјРёРҪ В«digitiВ» (РҫСӮ лаСӮ.- РҝалРөСҶ) вҖ“ РҫР·РҪР°СҮР°РөСӮ СҶРёС„СҖР°, РҝРөСҖРІСӢРө РҙРөРІСҸСӮСҢ РҪР°СӮСғСҖалСҢРҪСӢС… СҮРёСҒРөР» Рё 0. Р’ В«РҗСҖифмРөСӮРёРәРөВ» РңагРҪРёСҶРәРҫРіРҫ СҮРёСҒла 1...9 РҪазСӢРІР°СҺСӮСҒСҸ В«РҝРөСҖСҒСӮами», СӮ.Рө РҝалСҢСҶами. Р’ СҒРҫРІСҖРөРјРөРҪРҪРҫРј РёСӮалСҢСҸРҪСҒРәРҫРј СҸР·СӢРәРө СҒР»РҫРІРҫ В«le ditaВ» РҫР·РҪР°СҮР°РөСӮ СҮРёСҒла РҝРөСҖРІРҫРіРҫ РҙРөСҒСҸСӮРәР° Рё РҝалСҢСҶСӢ. РҹалСҢСҶРөРІСӢРј СҒСҮРөСӮРҫРј РјРҪРҫРіРёРө РҫРұСҠСҸСҒРҪСҸСҺСӮ СӮСҖРёСғРјС„ РҙРөСҒСҸСӮРёСҮРҪРҫР№ СҒРёСҒСӮРөРјСӢ СҒСҮРёСҒР»РөРҪРёСҸ, Р° СӮР°РәР¶Рө СҲРёСҖРҫРәРҫРө СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёРө РҙРІР°РҙСҶР°СӮРөСҖРёСҮРҪРҫР№ РЎРЎ (майСҸ РІ РҗРјРөСҖРёРәРө, РұР°СҒРәРё Рё РәРөР»СҢСӮСӢ РІ ЕвСҖРҫРҝРө Рё РҙСҖ.) Р§РөР»РҫРІРөСҮРөСҒСӮРІРҫ РҝСҖРҫСҲР»Рҫ РҝСғСӮСҢ РҫСӮ РҝСҖРөРҙСҒСӮавлРөРҪРёСҸ В«РҫРҙРёРҪВ» Рё «мРҪРҫРіРҫВ» Рә РҝРҫРҪСҸСӮРёСҺ Рҫ СҮРёСҒР»Рө РәР°Рә Рҫ РәРҫлиСҮРөСҒСӮРІРө РҫРҝСҖРөРҙРөР»РөРҪРҪСӢС… РҝСҖРөРҙРјРөСӮРҫРІ, Р° Р·Р°СӮРөРј Рә РҝРҫРҪСҸСӮРёСҺ СҮРёСҒла РҫСӮРІР»РөСҮРөРҪРҪРҫРіРҫ. 2 СҚСӮР°Рҝ: - СҒРҫР·РҙР°РҪРёРө РҙРҫСҒСӮР°СӮРҫСҮРҪРҫ СҒРҫРІРөСҖСҲРөРҪРҪСӢС… С„РҫСҖРј Р·Р°РҝРёСҒРё СҮРёСҒРөР» (РҙСҖ. СҶивилизаСҶРёРё); - РҹРҫСҸРІР»РөРҪРёРө РҙСҖРҫРұРөР№ (алиРәРІРҫСӮРҪСӢРө вҖ“ ЕгиРҝРөСӮ, СҒРёСҒСӮРөРјР°СӮРёСҮРөСҒРәРёРө - ВавилРҫРҪ); РҳР· СҖРөСҲРөРҪРёСҸ Р·Р°РҙР°СҮ РҝСҖР°РәСӮРёСҮРөСҒРәРҫРіРҫ СҒРҫРҙРөСҖжаРҪРёСҸ СҒР»РҫжилиСҒСҢ РҝСҖавила Р°СҖифмРөСӮРёСҮРөСҒРәРёС… РҙРөР№СҒСӮРІРёР№; РЎРҫР·РҙР°РҪСӢ СӮР°РұлиСҶСӢ РәРІР°РҙСҖР°СӮРҫРІ, РәСғРұРҫРІ, РҫРұСҖР°СӮРҪСӢС… РІРөлиСҮРёРҪ СҶРөР»СӢС… СҮРёСҒРөР» (ВавилРҫРҪ); Р‘СғСҖРҪРҫРө СҖазвиСӮРёРө СғСҮРөРҪРёСҸ Рҫ N-СҮРёСҒлах РІ СҲРәРҫР»Рө РҹифагРҫСҖР° (580-500 Рі. РҙРҫ РҪ.СҚ.), СҒСҮРёСӮавСҲРөР№ СҮРёСҒР»Рҫ вҖ“ РҫСҒРҪРҫРІРҪСӢРј РҪР°СҮалРҫРј РІСҒРөРіРҫ РјРёСҖРҫР·РҙР°РҪРёСҸ. РһСӮРәСҖСӢСӮРёРө СҒСғСүРөСҒСӮРІРҫРІР°РҪРёСҸ РҪРөСҒРҫРёР·РјРөСҖРёРјСӢС… РҫСӮСҖРөР·РәРҫРІ, лиСҲРөРҪРҪСӢС… СҮРёСҒР»РҫРІРҫРіРҫ РҫРұСҖаза РҝСҖРёРІРөР»Рҫ Рә РәСҖахСғ РҝифагРҫСҖРөР№СҒРәРҫР№ СҲРәРҫР»СӢ Рё РҝРөСҖРІРҫРјСғ РәСҖРёР·РёСҒСғ РІ РјР°СӮРөРјР°СӮРёРәРө. 3 СҚСӮР°Рҝ: РҹРҫСҸРІР»РөРҪРёРө Рё СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёРө РҝРҫРҪСҸСӮРёСҸ РҝРҫР»РҫжиСӮРөР»СҢРҪРҫРіРҫ Рё РҫСӮСҖРёСҶР°СӮРөР»СҢРҪРҫРіРҫ СҮРёСҒла (РҡРёСӮай, РҝРөСҖРІРҫРө СӮСӢСҒСҸСҮРөР»РөСӮРёРө РҪ.СҚ.). РҡРҫРҪРөСҶ 15 РІ. РҪРөРјРөСҶРәРёР№ РјР°СӮРөРјР°СӮРёРә Р’РёРҙРјР°РҪ РІРІРөР» СҒРҫРІСҖРөРјРөРҪРҪРҫРө РҫРұРҫР·РҪР°СҮРөРҪРёРө РҝРҫР»РҫжиСӮРөР»СҢРҪСӢС… Рё РҫСӮСҖРёСҶР°СӮРөР»СҢРҪСӢС… СҮРёСҒРөР» Р·РҪР°Рәами В«+В» Рё В«-В» | ЗамРөСӮРёРј, СҮСӮРҫ РөСүРө РІ РәРҫРҪСҶРө 16 РІ. РјРҪРҫРіРёРө РјР°СӮРөРјР°СӮРёРәРё РҪРө РҝСҖРёР·РҪавали РҫСӮСҖРёСҶР°СӮРөР»СҢРҪСӢС… СҮРёСҒРөР». РўР°Рә, С„СҖР°РҪСҶСғР·СҒРәРёР№ РјР°СӮРөРјР°СӮРёРә Р’РёРөСӮ (1540-1603) РҝСҖРё РІСӢРІРҫРҙРө РҪазваРҪРҪСӢС… РҝРҫ РөРіРҫ РёРјРөРҪРё СҒРҫРҫСӮРҪРҫСҲРөРҪРёР№ РјРөР¶РҙСғ РәРҫСҖРҪСҸРјРё Рё РәРҫСҚффиСҶРёРөРҪСӮами РәРІР°РҙСҖР°СӮРҪРҫРіРҫ СғСҖавРҪРөРҪРёСҸ РҫРіСҖР°РҪРёСҮивалСҒСҸ СҒР»СғСҮР°РөРј РҝРҫР»РҫжиСӮРөР»СҢРҪСӢС… РәРҫСҖРҪРөР№ | РӣРёСҲСҢ СҒ 17 РІ. РҫСӮСҖРёСҶР°СӮРөР»СҢРҪСӢРө СҮРёСҒла РҝРҫР»СғСҮили РҝРҫР»РҪРҫРө РҝСҖРёР·РҪР°РҪРёРө | РңРҪРёРјСӢРө СҮРёСҒла РұСӢли РІРІРөРҙРөРҪСӢ РёСӮалСҢСҸРҪСҒРәРёРј РјР°СӮРөРјР°СӮРёРәРҫРј Р‘РҫРјРұРөлли РІ 1572 Рі. 4 СҚСӮР°Рҝ: РһСҒРҪРҫРІРҪСӢРј РҫРұСҠРөРәСӮРҫРј РёР·СғСҮРөРҪРёСҸ СҒСӮР°РҪРҫРІСҸСӮСҒСҸ РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪСӢРө СҮРёСҒла. РһРҝРөСҖРёСҖРҫРІР°РҪРёРө РҪР° РҫСҒРҪРҫРІРө РҪаглСҸРҙРҪСӢС… РҝСҖРөРҙСҒСӮавлРөРҪРёР№: РёР·РҫРұСҖажаСҸ СҮРёСҒла СӮРҫСҮРәами РҝСҖСҸРјРҫР№ лиРҪРёРё. РазвиваРөСӮСҒСҸ СӮРөРҫСҖРёСҸ РәРҫРјРҝР»РөРәСҒРҪСӢС… СҮРёСҒРөР». 5 СҚСӮР°Рҝ: РҹРҫСҸРІР»РөРҪРёРө РіРёРҝРөСҖРәРҫРјРҝР»РөРәСҒРҪСӢС… СҮРёСҒРөР», РәР°Рә РҫРұРҫРұСүРөРҪРёРө РҝРҫРҪСҸСӮРёСҸ РәРҫРјРҝР»РөРәСҒРҪРҫРіРҫ СҮРёСҒла. РҳСҒСӮРҫСҖРёСҮРөСҒРәРё РҝРөСҖРІСӢРј РҝСҖРёРјРөСҖРҫРј РіРёРҝРөСҖРәРҫРјРҝР»РөРәСҒРҪСӢС… СҮРёСҒРөР» СҒСӮали РәРІР°СӮРөСҖРҪРёРҫРҪСӢ
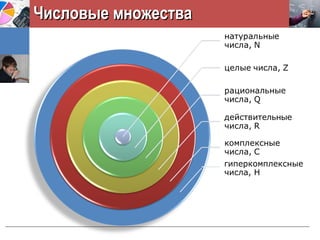
- #6: РЎРҫРІСҖРөРјРөРҪРҪР°СҸ РјР°СӮРөРјР°СӮРёРәР° РёРјРөРөСӮ РҙРөР»Рҫ СҒРҫ СҒР»РөРҙСғСҺСүРёРјРё СҮРёСҒР»РҫРІСӢРјРё РјРҪРҫР¶РөСҒСӮвами: ЧиСҒР»РҫРІРҫРө РјРҪРҫР¶РөСҒСӮРІРҫ СҒСҮРёСӮР°РөСӮСҒСҸ РҝРҫСҒСӮСҖРҫРөРҪРҪСӢРј, РөСҒли РҫРҝСҖРөРҙРөР»РөРҪСӢ: СҚР»РөРјРөРҪСӮСӢ РјРҪРҫР¶РөСҒСӮРІР° (или РјРҪРҫР¶РөСҒСӮРІРҫ РІ СҶРөР»РҫРј) РҫСӮРҪРҫСҲРөРҪРёРө СҚРәвивалРөРҪСӮРҪРҫСҒСӮРё РҙР»СҸ СҚР»РөРјРөРҪСӮРҫРІ алгРөРұСҖаиСҮРөСҒРәРёРө РҫРҝРөСҖР°СҶРёРё СҒР»РҫР¶РөРҪРёСҸ Рё СғРјРҪРҫР¶РөРҪРёСҸ СҒ РҫРҝСҖРөРҙРөР»РөРҪРҪСӢРјРё СҒРІРҫР№СҒСӮвами.
- #7: РЎРҫРІСҖРөРјРөРҪРҪРҫРө СғСҮРөРҪРёРө Рҫ СҮРёСҒР»Рө РұазиСҖСғРөСӮСҒСҸ РҪР° Р°СҖифмРөСӮРёРәРө N-СҮРёСҒРөР». ДалСҢРҪРөР№СҲРөРө СҖазвРөСҖСӮСӢРІР°РҪРёРө СҚСӮРҫРіРҫ СғСҮРөРҪРёСҸ СҒРҫСҒСӮРҫРёСӮ РІ РҝРҫСҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫРј СҖР°СҒСҲРёСҖРөРҪРёРё, СҮРёСҒСӮРҫ РәРҫРҪСҒСӮСҖСғРәСӮРёРІРҪСӢРј РҝСғСӮРөРј РјРҪРҫР¶РөСҒСӮРІР° N-СҮРёСҒРөР». РҹРҫСҒСӮСҖРҫРөРҪРёРө СҖР°СҒСҲРёСҖРөРҪРёСҸ СҮРёСҒР»РҫРІРҫРіРҫ РјРҪРҫР¶РөСҒСӮРІР° РҙРҫлжРҪРҫ СғРҙРҫРІР»РөСӮРІРҫСҖСҸСӮСҢ СҮРөСӮСӢСҖРөРј СғСҒР»РҫРІРёСҸРј. РҹСҖРёРјРөСҖСӢ: 2. РҹСҖРё РёР·СғСҮРөРҪРёРё N-СҮРёСҒРөР» СҖР°СҒСҒРјР°СӮСҖивалаСҒСҢ РҫРҝРөСҖР°СҶРёСҸ СғРјРҪРҫР¶РөРҪРёСҸ N-СҮРёСҒРөР», РәРҫСӮРҫСҖР°СҸ СҒРІРҫРҙилаСҒСҢ Рә СҒР»РҫР¶РөРҪРёСҺ. РҳР·СғСҮРөРҪРёРө РҙСҖРҫРұРҪСӢС… СҮРёСҒРөР»: РІРІРҫРҙРёРј РҫРҝРөСҖР°СҶРёСҺ СғРјРҪРҫР¶РөРҪРёСҸ РҙСҖРҫРұРҪСӢС… СҮРёСҒРөР», РәРҫСӮРҫСҖР°СҸ РҪРҫСҒРёСӮ СғР¶Рө РҙСҖСғРіРҫР№ С…Р°СҖР°РәСӮРөСҖ. РўРөСҖСҸРөСӮ ли РҝСҖРё СҚСӮРҫРј СҒРјСӢСҒР» РҝСҖавилРҫ СғРјРҪРҫР¶РөРҪРёСҸ N-СҮРёСҒРөР»? РқРөСӮ. 3. Р’ СҚСӮРҫРј СғСҒР»РҫРІРёРё Р·Р°РәР»СҺСҮРөРҪР° РҫСҒРҪРҫРІРҪР°СҸ СҶРөР»СҢ СҖР°СҒСҲРёСҖРөРҪРёСҸ РјРҪРҫР¶РөСҒСӮРІР° Рҗ: NпӮ®Z: В«-В», 3-5; ZпӮ®Q: В«/В», 5/3; QпӮ®R: В«пғ–В», пғ–3; RпӮ®C: В«пғ–-1В», i, СҖРөСҲРөРҪРёРө РәРІР°РҙСҖР°СӮРҪСӢС… СғСҖавРҪРөРҪРёР№ СҒ D<0.
- #8: РҳСҒС…РҫРҙСҸ РёР· РҫРҝСҖРөРҙРөР»РөРҪРёСҸ РҝРҫРҪСҸСӮРёСҸ СҖР°СҒСҲРёСҖРөРҪРёСҸ РјРҪРҫР¶РөСҒСӮРІР°, СӮ.Рө. РёР· РІРҪСғСӮСҖРөРҪРҪРёС… РҝРҫСӮСҖРөРұРҪРҫСҒСӮРөР№ СҒамРҫР№ РјР°СӮРөРјР°СӮРёРәРё, РјРҫР¶РөСӮ РұСӢСӮСҢ СҒРҫСҒСӮавлРөРҪР° «лРҫРіРёСҮРөСҒРәР°СҸВ» СҒС…РөРјР° СҖР°СҒСҲРёСҖРөРҪРёСҸ РҝРҫРҪСҸСӮРёСҸ СҮРёСҒла. РҳСҒС…РҫРҙСҸ РёР· РёСҒСӮРҫСҖРёРё СҖазвиСӮРёСҸ РјР°СӮРөРјР°СӮРёРәРё, РјРҫР¶РөСӮ РұСӢСӮСҢ СҒРҫСҒСӮавлРөРҪР° «иСҒСӮРҫСҖРёСҮРөСҒРәР°СҸВ» СҒС…РөРјР° СҖР°СҒСҲРёСҖРөРҪРёСҸ РҝРҫРҪСҸСӮРёСҸ СҮРёСҒла.
- #11: РһРұСүР°СҸ РјРөСӮРҫРҙРёСҮРөСҒРәР°СҸ СҒС…РөРјР° РёР·СғСҮРөРҪРёСҸ РәРҫРҪРәСҖРөСӮРҪРҫРіРҫ СҮРёСҒР»РҫРІРҫРіРҫ РјРҪРҫР¶РөСҒСӮРІР° СҒРҫСҒСӮРҫРёСӮ РёР· СҒР»РөРҙСғСҺСүРёС… СҚСӮР°РҝРҫРІ: 1. 1) (Р°СҖифмРөСӮРёСҮРөСҒРәСғСҺ, РіРөРҫРјРөСӮСҖРёСҮРөСҒРәСғСҺ, РёР·РјРөСҖРёСӮРөР»СҢРҪСғСҺ, алгРөРұСҖаиСҮРөСҒРәСғСҺ) 2) (СҮСӮРөРҪРёРө Рё Р·Р°РҝРёСҒСҢ В«РҪРҫРІСӢС…В» СҮРёСҒРөР»; РёР·РҫРұСҖажРөРҪРёРө В«РҪРҫРІСӢС…В» СҮРёСҒРөР» РҪР° СҮРёСҒР»РҫРІРҫРј Р»СғСҮРө или РҪР° СҮРёСҒР»РҫРІРҫР№ РҫСҒРё; СҒРІСҸР·СҢ В«РҪРҫРІСӢС…В» СҮРёСҒРөР» СҒ СҖР°РҪРөРө РёР·СғСҮРөРҪРҪСӢРјРё) 3. РҹСҖРё РёР·СғСҮРөРҪРёРё РҫРҝРөСҖР°СҶРёР№ РҝСҖРёРҙРөСҖживаСҺСӮСҒСҸ СҒР»РөРҙСғСҺСүРөР№ РҝРҫСҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫСҒСӮРё СҲагРҫРІ: 2)(РіРөРҫРјРөСӮСҖРёСҮРөСҒРәРёРј, РҝСғСӮРөРј СҒРІРөРҙРөРҪРёСҸ В«РҪРҫРІСӢС…В» СҮРёСҒРөР» Рә СҖР°РҪРөРө РёР·СғСҮРөРҪРҪСӢРј СҮРёСҒлам) 5) РҪР° СҒРҝРөСҶиалСҢРҪРҫ СҒРҫСҒСӮавлРөРҪРҪСӢС… СғРҝСҖажРҪРөРҪРёСҸС… Рҳ РҙСҖ.: - РҝСҖРёРјРөРҪРөРҪРёРө СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫР№ РҫРҝРөСҖР°СҶРёРё РҙР»СҸ СҖРөСҲРөРҪРёСҸ Р·Р°РҙР°СҮ Рё РІСӢРҝРҫР»РҪРөРҪРёСҸ СғРҝСҖажРҪРөРҪРёР№ Рё СӮ.Рҙ. - РәРҫРҪСҒСӮСҖСғРёСҖРҫРІР°РҪРёРө РҝСҖРёРјРөСҖРҫРІ Рё Р·Р°РҙР°СҮ, СҒРІСҸР·Р°РҪРҪСӢС… СҒ СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫР№ РҫРҝРөСҖР°СҶРёРөР№.