Р»РөРәСҶРёСҸ 29
- 1. РӣРөРәСҶРёСҸ в„– 29. Р“СҖР°РҪРёСҮРҪСӢРө СғСҒР»РҫРІРёСҸ РҙР»СҸ СҖР°СҒСҮРөСӮР° СҖР°РҙиалСҢРҪСӢС… СҒРёР» 02/26/14 1
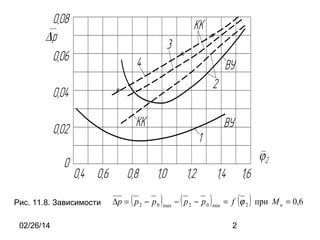
- 2. Р РёСҒ. 11.8. ЗавиСҒРёРјРҫСҒСӮРё 02/26/14 ( вҲҶСҖ = СҖ 2 вҲ’ СҖ 0 ) max ( вҲ’ СҖ2 вҲ’ СҖ0 ) min ( ) = f П• 2 РҝСҖРё Рң Рё = 0,6 2
- 3. b2 ОІР»2 1вҖ“СҒСӮСғРҝРөРҪСҢ СҒ Р’РЈ 32Рҫ r4 r РҪР°СҖ BРә = 0,05 1,6 1,73 BРә D2 - в„Ұ вҲҶСҖ РҪР° r = 1 0,72 2вҖ“СҒСӮСғРҝРөРҪСҢ СҒ РҡРҡ 38 Рҫ 0,054 1,45 1,72 0,37 0,67 3вҖ“СҒСӮСғРҝРөРҪСҢ СҒ РҡРҡ 45Рҫ 0,066 1,59 1,69 0,42 0,66 4вҖ“СҒСӮСғРҝРөРҪСҢ РҡРҡ 45Рҫ 0,068 1,52 1,67 0,34 вҲҶСҖ РҪР° r = 1,08 0,65 02/26/14 РҝСҖРІРөРҙРөРҪРҫ Рә r =1 вҲҶСҖ РҪР° r = 1 БДРҡРҗ2 вҲҶСҖ РҪР° r = 1 3
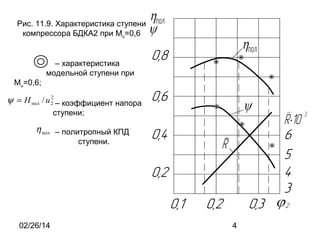
- 4. Р РёСҒ. 11.9. РҘР°СҖР°РәСӮРөСҖРёСҒСӮРёРәР° СҒСӮСғРҝРөРҪРё РәРҫРјРҝСҖРөСҒСҒРҫСҖР° БДРҡРҗ2 РҝСҖРё Mu=0,6 вҖ“ С…Р°СҖР°РәСӮРөСҖРёСҒСӮРёРәР° РјРҫРҙРөР»СҢРҪРҫР№ СҒСӮСғРҝРөРҪРё РҝСҖРё Mu=0,6; 2 ПҲ = Рқ РҝРҫР» / Рё 2 вҖ“ РәРҫСҚффиСҶРёРөРҪСӮ РҪР°РҝРҫСҖР° СҒСӮСғРҝРөРҪРё; О· РҝРҫР» вҖ“ РҝРҫлиСӮСҖРҫРҝРҪСӢР№ РҡРҹР” СҒСӮСғРҝРөРҪРё. 02/26/14 4
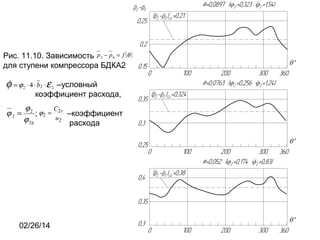
- 5. Р РёСҒ. 11.10. ЗавиСҒРёРјРҫСҒСӮСҢ СҖ 2 вҲ’ СҖ 0 = f (Оё ) РҙР»СҸ СҒСӮСғРҝРөРҪРё РәРҫРјРҝСҖРөСҒСҒРҫСҖР° БДРҡРҗ2 ПҶ =П• П•2 = 2 вӢ… 4 вӢ… b 2 вӢ… Оө 2 вҖ“СғСҒР»РҫРІРҪСӢР№ РәРҫСҚффиСҶРёРөРҪСӮ СҖР°СҒС…РҫРҙР°, П•2 РЎ ; П•2 = 2r вҖ“РәРҫСҚффиСҶРёРөРҪСӮ u2 П• 2СҖ СҖР°СҒС…РҫРҙР° 02/26/14 5
- 6. РһСҒСҖРөРҙРҪРөРҪРҪСӢРө РҝРҫ СҲРёСҖРёРҪРө bвҖҷ2 завиСҒРёРјРҫСҒСӮРё РҫРәСҖСғР¶РҪРҫР№ C2u(Оё) Рё СҖР°РҙиалСҢРҪРҫР№ C2r(Оё) СҒРҫСҒСӮавлСҸСҺСүРёС… Р°РұСҒРҫР»СҺСӮРҪРҫР№ СҒРәРҫСҖРҫСҒСӮРё Р·Р° Р Рҡ РҙР»СҸ РёСҒРҝРҫР»СҢР·РҫРІР°РҪРёСҸ РІ СғСҖавРҪРөРҪРёСҸС… (11.15) Рё (11.16) РҝСҖРёРҪСҸСӮСӢ РҝРҫ СҖРөРәРҫРјРөРҪРҙР°СҶРёСҸРј Р“. Рқ. Р”РөРҪР°. Р’ РұРөР·СҖазмРөСҖРҪРҫРј РІРёРҙРө завиСҒРёРјРҫСҒСӮСҢ C2u(Оё) РёРјРөРөСӮ РІРёРҙ C 2u ( Оё ) = ОЁ2 вӢ… 1 + 2 2 ОЁ2 [( СҖ 2 2ПҖ пЈ® 1 2 + 2пЈҜ1 вҲ’ 1+ 2 СҖ2 вҲ’ СҖ0 вҲ« ПҲ2 пЈ° 2ПҖ 0 [( 02/26/14 вҲ’ СҖ 0 ) СҒСҖ вҲ’ ( СҖ 2 вҲ’ СҖ 0 ) ] (11.20) ) вҲ’(СҖ СҒСҖ 2 вҲ’ СҖ0 )] пЈ№ вӢ… dОё пЈә. пЈ» 6
- 7. ЗавиСҒРёРјРҫСҒСӮСҢ C2r(Оё) РҙР»СҸ СҖРөСҲРөРҪРёСҸ СғСҖавРҪРөРҪРёР№ (11.15) Рё (11.16) РҫРҝСҖРөРҙРөР»РөРҪР° РІ РІРёРҙРө РЎ 2 r (Оё ) = Рә вӢ… РЎ 2 r (Оё ) Рҝ . (11.22) Р—РҪР°СҮРөРҪРёСҸ C2r(Оё)Рҝ РҪахРҫРҙСҸСӮСҒСҸ РёР· СғСҖавРҪРөРҪРёСҸ СҒРҫС…СҖР°РҪРөРҪРёСҸ РІРёС…СҖСҸ РЎ 2 r (Оё ) Рҝ РіРҙРө I Рә (Оё ) = r РҪР°СҖ вҲ« 1 b dr r [ ] d = РЎ 2Рё (Оё ) вӢ… I Рә (Оё ) , dОё (11.23) вҖ“ РёРҪСӮРөРіСҖал СҒРөСҮРөРҪРёР№ Р‘РӣР” (РҪР° СҖР°РҙРёСғСҒах Рё, СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ, СҲРёСҖРёРҪах b = b вҖІ 2 Г· b 3 ) Рё Р’РЈ или РҡРҡ (РҪР° СҖР°РҙРёСғСҒах r РІРҪ r РҪР°СҖ Рё, СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ, СҲРёСҖРёРҪах b = b 3 Г· B РҪ ) РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ B b СҮРёСҒР»РөРҪРҪРҫ РҙР»СҸ РІСҒРөС… Р·Р°РҙР°РҪРҪСӢС… Р·РҪР°СҮРөРҪРёР№ Сғгла Оё, b = , B = . вҖІ вҖІ b2 b2 02/26/14 7 r = r3



![РһСҒСҖРөРҙРҪРөРҪРҪСӢРө РҝРҫ СҲРёСҖРёРҪРө bвҖҷ2 завиСҒРёРјРҫСҒСӮРё РҫРәСҖСғР¶РҪРҫР№ C2u(Оё) Рё
СҖР°РҙиалСҢРҪРҫР№ C2r(Оё) СҒРҫСҒСӮавлСҸСҺСүРёС… Р°РұСҒРҫР»СҺСӮРҪРҫР№ СҒРәРҫСҖРҫСҒСӮРё Р·Р° Р Рҡ РҙР»СҸ
РёСҒРҝРҫР»СҢР·РҫРІР°РҪРёСҸ РІ СғСҖавРҪРөРҪРёСҸС… (11.15) Рё (11.16) РҝСҖРёРҪСҸСӮСӢ РҝРҫ СҖРөРәРҫРјРөРҪРҙР°СҶРёСҸРј
Р“. Рқ. Р”РөРҪР°. Р’ РұРөР·СҖазмРөСҖРҪРҫРј РІРёРҙРө завиСҒРёРјРҫСҒСӮСҢ C2u(Оё) РёРјРөРөСӮ РІРёРҙ
C 2u ( Оё ) = ОЁ2 вӢ… 1 +
2
2
ОЁ2
[( СҖ
2
2ПҖ
пЈ®
1
2
+ 2пЈҜ1 вҲ’
1+ 2 СҖ2 вҲ’ СҖ0
вҲ« ПҲ2
пЈ° 2ПҖ 0
[(
02/26/14
вҲ’ СҖ 0 ) СҒСҖ вҲ’ ( СҖ 2 вҲ’ СҖ 0 )
]
(11.20)
) вҲ’(СҖ
СҒСҖ
2
вҲ’ СҖ0
)]
пЈ№
вӢ… dОё пЈә.
пЈ»
6](https://image.slidesharecdn.com/29-140226033527-phpapp01/85/29-6-320.jpg)
![ЗавиСҒРёРјРҫСҒСӮСҢ C2r(Оё) РҙР»СҸ СҖРөСҲРөРҪРёСҸ СғСҖавРҪРөРҪРёР№ (11.15) Рё (11.16)
РҫРҝСҖРөРҙРөР»РөРҪР° РІ РІРёРҙРө
РЎ 2 r (Оё ) = Рә вӢ… РЎ 2 r (Оё ) Рҝ .
(11.22)
Р—РҪР°СҮРөРҪРёСҸ C2r(Оё)Рҝ РҪахРҫРҙСҸСӮСҒСҸ РёР· СғСҖавРҪРөРҪРёСҸ СҒРҫС…СҖР°РҪРөРҪРёСҸ РІРёС…СҖСҸ
РЎ 2 r (Оё ) Рҝ
РіРҙРө
I Рә (Оё ) =
r РҪР°СҖ
вҲ«
1
b
dr
r
[
]
d
=
РЎ 2Рё (Оё ) вӢ… I Рә (Оё ) ,
dОё
(11.23)
вҖ“ РёРҪСӮРөРіСҖал СҒРөСҮРөРҪРёР№ Р‘РӣР” (РҪР° СҖР°РҙРёСғСҒах Рё,
СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ, СҲРёСҖРёРҪах b = b вҖІ 2 Г· b 3 ) Рё Р’РЈ или РҡРҡ (РҪР° СҖР°РҙРёСғСҒах
r РІРҪ r РҪР°СҖ Рё, СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ, СҲРёСҖРёРҪах b = b 3 Г· B РҪ ) РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ
B
b
СҮРёСҒР»РөРҪРҪРҫ РҙР»СҸ РІСҒРөС… Р·Р°РҙР°РҪРҪСӢС… Р·РҪР°СҮРөРҪРёР№ Сғгла Оё, b = , B =
.
вҖІ
вҖІ
b2
b2
02/26/14
7
r = r3](https://image.slidesharecdn.com/29-140226033527-phpapp01/85/29-7-320.jpg)