![B-部分点実装
● open[i] = 时刻颈にドアが开いているかどうか](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-10-320.jpg)
![B-部分点実装
● open[i] = 时刻颈にドアが开いているかどうか
● 時刻aに人が通りかかった
– open[a], open[a+1], … , open[a + t – 1]をTrueに
する](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-11-320.jpg)
![B-部分点実装
● open[i] = 时刻颈にドアが开いているかどうか
● 時刻aに人が通りかかった
– open[a], open[a+1], … , open[a + t – 1]をTrueに
する
● 最後にopen[i] = Trueであるiを数える](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-12-320.jpg)
![B-部分点実装
● open[i] = 时刻颈にドアが开いているかどうか
● 時刻aに人が通りかかった
– open[a], open[a+1], … , open[a + t – 1]をTrueに
する
● 最後にopen[i] = Trueであるiを数える
● O(NT) 50点獲得](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-13-320.jpg)
![B-満点解法
● close[i] = 時刻iの時点でドアが何秒後に閉まる
予定か？](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-14-320.jpg)
![B-満点解法
● close[i] = 時刻iの時点でドアが何秒後に閉まる
予定か？
● 時刻aに人が通りかかった
– close[a] = T](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-15-320.jpg)
![B-満点解法
● close[i] = 時刻iの時点でドアが何秒後に閉まる
予定か？
● 時刻aに人が通りかかった
– close[a] = T
● 時刻aに人が通らなかった
– close[a] = max(close[a-1] – 1, 0)](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-16-320.jpg)
![B-満点解法
● close[i] = 時刻iの時点でドアが何秒後に閉まる
予定か？
● 時刻aに人が通りかかった
– close[a] = T
● 時刻aに人が通らなかった
– close[a] = max(close[a-1] – 1, 0)
● 最後にclose[i] > 0であるiを数える](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-17-320.jpg)
![B-満点解法
● close[i] = 時刻iの時点でドアが何秒後に閉まる
予定か？
● 時刻aに人が通りかかった
– close[a] = T
● 時刻aに人が通らなかった
– close[a] = max(close[a-1] – 1, 0)
● 最後にclose[i] > 0であるiを数える
● O(時刻)](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-18-320.jpg)
![C-問題概要
● 1～Nの番号が付けられた街がある
● i(1 ≦ i ≦ D)日目にはL[i] ≦ 街番号 ≦ R[i]となる
街の間でのみ行き来が可能である。
● 民族i(1 ≦ i ≦ K)は街S[i]から街T[i]に移動したい
● 各民族はできるだけ早く目的地に到着するよう
に移動する
● 各民族が目的地に着く日を求めよ](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-20-320.jpg)
![C-考察
● i(1 ≦ i ≦ D)日目にはL[i] ≦ 街番号 ≦ R[i]となる
街の間でのみ行き来が可能である。
● この移動制限の性質から、街は以下のように一
直線に並んでいると考えても良い](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-21-320.jpg)
![C-考察
● i(1 ≦ i ≦ D)日目にはL[i] ≦ 街番号 ≦ R[i]となる
街の間でのみ行き来が可能である。
● この移動制限の性質から、街は以下のように一
直線に並んでいると考えても良い
● このうち一区間が移動可能と捉えることが出来
る (L[i] = 4, R[i] = 7の例)](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-22-320.jpg)
![C-考察
● i(1 ≦ i ≦ D)日目にはL[i] ≦ 街番号 ≦ R[i]となる
街の間でのみ行き来が可能である。
● この移動制限の性質から、街は以下のように一
直線に並んでいると考えても良い
● このうち一区間が移動可能と捉えることが出来
る (L[i] = 6, R[i] = 9の例)](https://image.slidesharecdn.com/abc024-150523140045-lva1-app6891/85/AtCoder-Beginner-Contest-024-23-320.jpg)
More Related Content
What's hot (20)
Viewers also liked (16)
More from AtCoder Inc. (18)
Recently uploaded (10)
AtCoder Beginner Contest 024 解説
- 2. A-問題概要 ● 動物園の入場料の情報が与えられる – 子供1人 A 円 – 大人1人 B 円 – K人以上の団体は1人当たりC円引 ● 子供S人、大人T人の団体が支払わなければなら ない入場料はいくらか求めよ
- 3. A-問題概要 ● 団体の人数がK以上かK未満かで場合分けして 計算する ● 人数がK以上の時 – 入場料＝A*S + B*T – C*(S+T) ● 人数がK未満の時 – 入場料＝A*S + B*T
- 4. A-注意 ● この手の問題は「以上」か「超える」か注意し ましょう ● 実装時に < と ≦ を間違えてWrongAnswerとい うのはもったいないです
- 6. B-問題概要 ● 前を人が通りかかるとT秒開き続ける自動ドア がある ● 開いている途中に新たに人が通りかかったら開 く時間がそこからT秒後まで延長される ● N人がドアの前を通りかかった時刻が与えられ る ● ドアが開いていた合計秒数を求めよ
- 7. B-部分点解法 ● N ≦ 10^5 ● T ≦ 100 ● 時刻 ≦ 10^6
- 8. B-部分点解法 ● N ≦ 10^5 ● T ≦ 100 ● 時刻 ≦ 10^6 ● 各時刻についてその時刻にドアが開いていたか 閉まっていたか覚えておく
- 9. B-部分点解法 ● N ≦ 10^5 ● T ≦ 100 ● 時刻 ≦ 10^6 ● 各時刻についてその時刻にドアが開いていたか 閉まっていたか覚えておく ● 人が通りかかると、その時刻からT秒間のドア は開き続ける
- 10. B-部分点実装 ● open[i] = 时刻颈にドアが开いているかどうか
- 11. B-部分点実装 ● open[i] = 时刻颈にドアが开いているかどうか ● 時刻aに人が通りかかった – open[a], open[a+1], … , open[a + t – 1]をTrueに する
- 12. B-部分点実装 ● open[i] = 时刻颈にドアが开いているかどうか ● 時刻aに人が通りかかった – open[a], open[a+1], … , open[a + t – 1]をTrueに する ● 最後にopen[i] = Trueであるiを数える
- 13. B-部分点実装 ● open[i] = 时刻颈にドアが开いているかどうか ● 時刻aに人が通りかかった – open[a], open[a+1], … , open[a + t – 1]をTrueに する ● 最後にopen[i] = Trueであるiを数える ● O(NT) 50点獲得
- 14. B-満点解法 ● close[i] = 時刻iの時点でドアが何秒後に閉まる 予定か？
- 15. B-満点解法 ● close[i] = 時刻iの時点でドアが何秒後に閉まる 予定か？ ● 時刻aに人が通りかかった – close[a] = T
- 16. B-満点解法 ● close[i] = 時刻iの時点でドアが何秒後に閉まる 予定か？ ● 時刻aに人が通りかかった – close[a] = T ● 時刻aに人が通らなかった – close[a] = max(close[a-1] – 1, 0)
- 17. B-満点解法 ● close[i] = 時刻iの時点でドアが何秒後に閉まる 予定か？ ● 時刻aに人が通りかかった – close[a] = T ● 時刻aに人が通らなかった – close[a] = max(close[a-1] – 1, 0) ● 最後にclose[i] > 0であるiを数える
- 18. B-満点解法 ● close[i] = 時刻iの時点でドアが何秒後に閉まる 予定か？ ● 時刻aに人が通りかかった – close[a] = T ● 時刻aに人が通らなかった – close[a] = max(close[a-1] – 1, 0) ● 最後にclose[i] > 0であるiを数える ● O(時刻)
- 19. ABC024解説 C:民族大移動
- 20. C-問題概要 ● 1～Nの番号が付けられた街がある ● i(1 ≦ i ≦ D)日目にはL[i] ≦ 街番号 ≦ R[i]となる 街の間でのみ行き来が可能である。 ● 民族i(1 ≦ i ≦ K)は街S[i]から街T[i]に移動したい ● 各民族はできるだけ早く目的地に到着するよう に移動する ● 各民族が目的地に着く日を求めよ
- 21. C-考察 ● i(1 ≦ i ≦ D)日目にはL[i] ≦ 街番号 ≦ R[i]となる 街の間でのみ行き来が可能である。 ● この移動制限の性質から、街は以下のように一 直線に並んでいると考えても良い
- 22. C-考察 ● i(1 ≦ i ≦ D)日目にはL[i] ≦ 街番号 ≦ R[i]となる 街の間でのみ行き来が可能である。 ● この移動制限の性質から、街は以下のように一 直線に並んでいると考えても良い ● このうち一区間が移動可能と捉えることが出来 る (L[i] = 4, R[i] = 7の例)
- 23. C-考察 ● i(1 ≦ i ≦ D)日目にはL[i] ≦ 街番号 ≦ R[i]となる 街の間でのみ行き来が可能である。 ● この移動制限の性質から、街は以下のように一 直線に並んでいると考えても良い ● このうち一区間が移動可能と捉えることが出来 る (L[i] = 6, R[i] = 9の例)
- 24. C-例 1つの民族について考える
- 25. C-例 1日目
- 26. C-例 2日目:移動せず
- 27. C-例 3日目
- 28. C-例 4日目:移動せず
- 29. C-例 5日目:目的地に到着
- 31. C-考察 ● 街が一直線に並んでいるので、民族はSとTの間 のすべての街を通過しなければならない ● 民族は近づく方向にのみ進めば良い – 再び同じ所に帰ってくるならば、その間移動しなく てもよい
- 32. C-考察 ● 街が一直線に並んでいるので、民族はSとTの間 のすべての街を通過しなければならない ● 民族は近づく方向にのみ進めば良い – 再び同じ所に帰ってくるならば、その間移動しなく てもよい ● 近づけるだけ近づいたほうが良い – 進みすぎたせいで、他の移動方法より近づけないと いうことはない →
- 33. C-考察 ● 街が一直線に並んでいるので、民族はSとTの間 のすべての街を通過しなければならない ● 民族は近づく方向にのみ進めば良い – 再び同じ所に帰ってくるならば、その間移動しなく てもよい ● 近づけるだけ近づいたほうが良い – 進みすぎたせいで、他の移動方法より近づけないと いうことはない →貪欲法
- 34. C-貪欲法 ● 先程の例
- 40. C-想定解法 ● 各民族について別々に到達日を求める ● 1日目から順番にTにできるだけ近づくように移 動する – 始めてTに到着する日が答え ● O(DK)
- 41. ABC024解説 D:動的計画法
- 42. D-問題概要 ● 10^8 × 10^8の方眼紙の上で有名な動的計画法 の問題を解く – 左下のマスから開始して右、上に1マス動くという のを繰り返して各マスに到達する方法の個数を MOD 1,000,000,007で求めよ – その答えを各マスに書き込む ● 左からxマス下からyマスの位置を(x, y) とする ● マス(r, c), (r, c + 1), (r + 1, c)に書かれている整 数を元にr, cを求めよ
- 43. D-有名事実 ● (r, c)に書かれている値は である – (0, 0) から (r, c)に到達するまでに r+c回の移動を行 う – そのうちr回が右向きの移動 – r+c回のうちどのr回に右向きの移動を行うか数えれ ば良い –
- 44. D-問題概要言い換え ● 、 、 が与え られる – ただし1,000,000,007で割った余り) ● r, cを求めよ – 0 ≦ r, c ＜ 99,999,999が保証されている
- 45. D-問題概要言い換え ● 、 、 が与え られる – ただし1,000,000,007で割った余り) ● r, cを求めよ – 0 ≦ r, c ＜ 99,999,999が保証されている ● k = r+cとすると
- 46. D-問題概要言い換え ● 、 、 が与え られる – ただし1,000,000,007で割った余り) ● r, cを求めよ – 0 ≦ r, c ＜ 99,999,999が保証されている ● k = r+cとすると ● 、 、 が与えられる ● k-c, cを求めよ
- 52. D-式変形 ● 両辺を1から引く
- 54. 顿-整理して
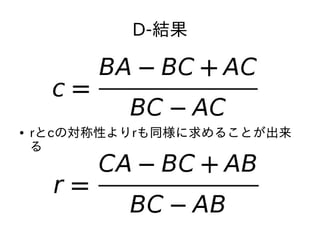
- 56. 顿-结果
- 58. D-注意 ● r, cを求める式は四則演算のみで構成されてい る。 ● 途中で1,000,000,007の倍数で割ることがなけ ればMOD 1,000,000,007 しても結果は変わら ない
- 59. D-MODでの演算 ● 1,000,000,007は素数なのでこれでMODを とっても四則演算が実行できる ● 以下 法を1,000,000,007として、A ≡ a, B ≡ b, C ≡ cとする ● 足し算、引き算 – A ± B = Cならば a ± b ≡ c ● 掛け算 – A × B = Cならば a × b ≡ c
- 60. D-MODでの演算 ● 以下 法を1,000,000,007として、A ≡ a, B ≡ b, C ≡ cとする ● 割り算 – B ≡ 0でなくA ÷ B = Cならば a × (bの逆元) ≡ c ● 逆元とは – Xの逆元とは X × Y ≡ 1となるYのこと – X≠0 で 法(ここでは1,000,000,007)が素数ならば 逆元が唯一つ存在する – →常に割り算が出来る
- 61. D-逆元の求め方 ● 法が素数Pのときの逆元は容易に求めることが 出来る ● フェルマーの小定理より以下の関係式が導ける (証明割愛) ● 今回ならばある値を 1,000,000,005乗すれば その逆元が求まる
- 62. D-高速に累乗を求める ● 1,000,000,005乗はどのように求めればよいだ ろうか？ – 愚直に掛け算を繰り返すとTLEしてしまう ● X^Nを高速に求める以下の様なアルゴリズムが ある – を予め求める – Nを2進数表記することを考えると上記の予め求め た値の積でX^Nを求めることが出来る – Nの2進数表記はO(logN)桁なので計算量もO(logN) – 速い
- 63. D-想定解法 ● この計算をMOD 1,000,000,007の中で行う – 割り算は逆元を利用する ● 答えとなるrとcのMOD 1,000,000,007が求ま る ● 0 ≦ r, c ＜ 99,999,999なのでr, cは一意に定ま る ● それが出力する答え