狠狠撸

Chapter 4 　横浜国立大学　 D1 　柴田泰宙　 Parameterization

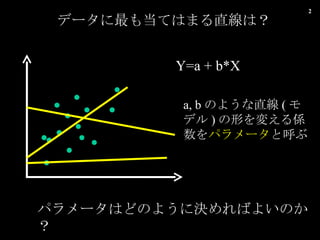
データに最も当てはまる直線は？ Y=a + b*X a, b のような直線 ( モデル ) の形を変える係数をパラメータと呼ぶパラメータはどのように決めればよいのか？

数理モデルを構築するに当たっては、パラメータや定数が必要それらを得るための方法 4.1. 生データそのまま 4.2. 生データを変換してから 4.3. 生データを変換して、モデルも試行錯誤

4.1. 生データそのまま最も直接的 (Y=X なモデル ) ( 当たり前だが ) パラメータは推定されるものであることに留意 4.2. 生データを変換してから先行研究に従って変換 ( 事例では log(Y)=log(X)) しかし、その変換がいつでも最良とは限らない

4.3. 生データを変換して、モデルも試行錯誤観測値と予測値の差が最小になるように、パラメータを調整重みつき残差平方和 error は、 i 番目のデータの持つ分散としている (i 番目のデータは j 個のデータの平均値扱い ) データ多 ->分散小-> Cost 大->だから、ズレちゃだめ (AIC 的には??? )

4.3.1 線形回帰基本形指数逆数指数 2 ( 教科書と違う )

4. 3. 2 非線形回帰非線形の定義は？線形でないこと線形モデルに比べ、最も ModelCost の低い点が見つけにくいので、初期値を変えて試す必要あり本当に見つけにくい？ ( 例は当てはめただけでつまらないので勝手に ) 初期値を乱数で変えてみた

[198,] 10.435 1.60 209.633 [199,] 45.229 -1.60 -209.632 [200,] 5.284 12.12 -70.093 [201,] 10.435 1.60 209.632 [1,] 10.435 1.60 209.632 [2,] 10.435 1.60 209.633 [3,] 10.435 1.60 209.632 ??? ??? ← 本 (p125) と一緒の値初期値が悪いと確かに良くないようだ 4. 4 ケーススタディ 4.4.1 P-I カーブ

4.4.2 線形モデル vs 非線形モデル P126 の (4. 10) 式を線形モデルと非線形モデル、両方でパラメータ推定します ((4.10) 式の導出は Appendix 1) 線形モデルのモデル式非線形モデルのモデル式と置くただし

sum(LL$residuals^2) [1] 0.1073133 sum(summary(fit)$residuals^2) [1] 0.08434943 残差平方和は非線形回帰の方が小さかった ( 教科書は x 軸と y 軸が逆転してて非常に見にくいので、勝手に変えました .Appendix2) 線形モデル ( 赤 ) 非線形モデル ( 青 ) 大きな x と小さな x で当てはまりに差

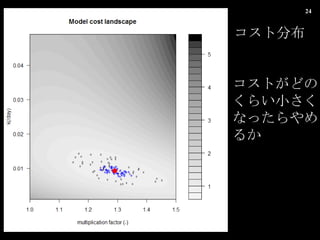
4.4.3 疑似乱数によるパラメータ探索手順 1. たくさんのパラメータ候補を発生させる 2. それらのパラメータを使った ModelCost を計算 3. パラメータをいくつか選んでその平均値を計算 4. もう一つ別のパラメータを選んで、それを軸に対称にあるパラメータを選択 5. そのパラメータの ModelCost が一番悪い ModelCost より小さければ採択

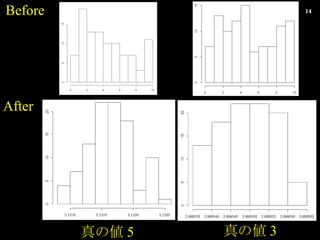
例 (p133 のやつはコードを打てばできるので ) Y = a + bX のパラメータ a と b を推定してみる (Appendix3) 1. たくさんのパラメータ候補を発生させる a2 <- runif(100, 0, 10) b2 <- runif(100, 0, 10) 2. それらのパラメータを使った ModelCost を計算この場合、 100 個の ModelCost が計算される a <- 5 b <- 3

3. パラメータをいくつか選んでその平均値を計算 a_mean <- mean(sample(a2, 3)) 4. もう一つ別のパラメータを選んで、それを軸に対称にあるパラメータを選択 ( 例えば、 a_mean が 5 だったとして、 a_mirror が 3 だとすると、 2*5-3=7 となり、 3 を中心に等しい距離 (2) だけ移動したことになる。局所解にトラップされない工夫だと思われる ) a_mirror <- sample(a2, 1) new_a <- 2*a_mean - a_mirror 5. そのパラメータの ModelCost が一番悪い ModelCost より小さければ採択最適解だけ求めようとしていることに留意

真の値 5 真の値 3 Before After

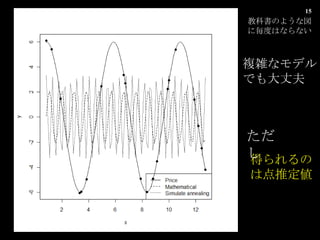
複雑なモデルでも大丈夫得られるのは点推定値ただし教科书のような図に毎度はならない

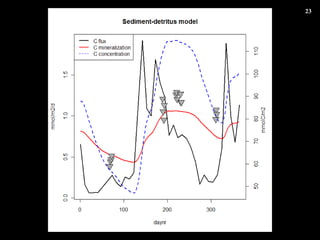
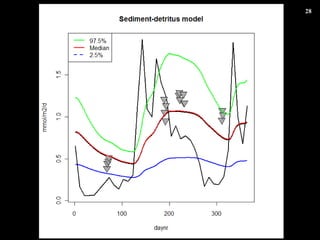
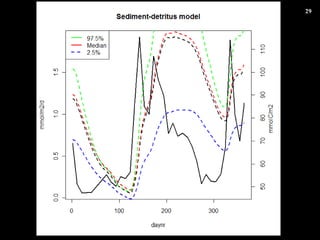
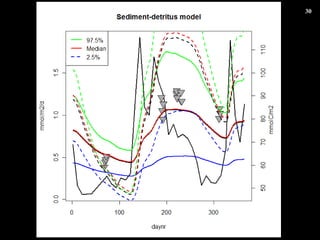
4.4.4 　先ほどのアルゴリズムを使って、微分方程式　　　　のパラメータ推定 http://geos.ees.hokudai.ac.jp/noriki/Trap.html セジメントトラップ海水中を沈降する粒子を集める装置今回は、有機炭素がどのように無機炭素に石灰化していくのかモデリングしてみる有機?無機炭素量 ( flux ) 酸素消費量 ( oxycon ) 上記の時間軸 < 手持ちのデータは 3 つ >

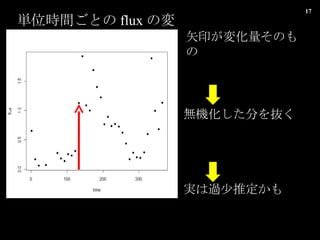
単位時間ごとの flux の変化矢印が変化量そのもの無機化した分を抜く実は過少推定かも

パラメータ推定の流れ 1. 観測値と微分方程式からの予測値の差を最小にするようにパラメータ k, mult を推定する .flux の値は offset のように強制的に与えた 2. 得られたパラメータで、もう一度微分方程式に当てはめる 3. 予測値をプロットしてみて、実際のものと合っているか確認

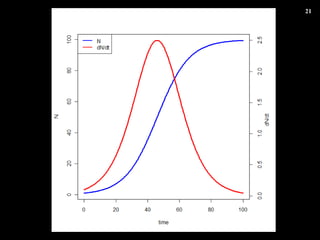
ちょっと説明： R で微分方程式 ode 関数 (Ordinary differential equation) を使用 ode( 初期値、時間、微分方程式、パラメータ ) < 用法 > 例 : 個体群増加モデルを解いてみる (Appendix 4) N は個体数、 r は増加率、 K は環境収容力ロジスティックモデル

Growth_model <- function ( t , state, pars) { with (as.list(c(state, pars)), { dN <- r * N *(K - N)/K return(list(dN, r * N *(K - N)/K))}) } pars <- c(r=0.3, K=100) ini <- c(N=1) times <- seq(0, 100) out <- as.data.frame(ode(func= Growth_model , y= ini , parms= pars , times= times )) 微分方程式作成初期値とパラメータ微分方程式解かせる

minmod <- function(t, Carbon, parameters) { with(as.list(c(Carbon, parameters)), { minrate <- k*Carbon Depo <- approx(Flux[, 1], Flux[, 2], xout=t)$y dCarbon <- mult*Depo - minrate list(dCarbon, minrate) }) } 時刻 t での flux を与えている costt <- sum((minrate- oxcon$cons)^2) …

コストがどのくらい小さくなったらやめるかコスト分布

第四章のまとめ線形回帰と非線形回帰を紹介した非線形回帰の初期値依存の様子を示したコストをあらかじめ計算して、良さそうなパラメータからスタートする重要性の示唆ミラー関数 (Price 関数 ) でパラメータ推定することの有効性の示唆

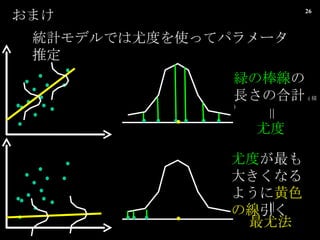
おまけ統計モデルでは尤度を使ってパラメータ推定緑の棒線の長さの合計 ( 積 ) 尤度尤度が最も大きくなるように黄色の線引く最尤法＝＝

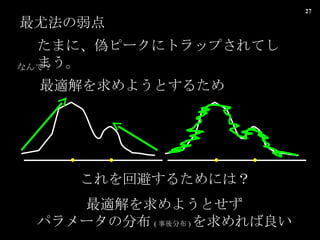
最尤法の弱点たまに、偽ピークにトラップされてしまう。これを回避するためには？最適解を求めようとするためなんで？最適解を求めようとせずパラメータの分布 ( 事後分布 ) を求めれば良い

誤差を考慮することで、不確実性を見積もることができるおまけのまとめ最適解を追い求める以外のアルゴリズムでも、同じ結論になる個人的には、パラメータには誤差があるものとして扱ってほしいこともある現実的に無理な場合が多々ありますし

狠狠撸

Model seminar shibata_100710

Recommended

More Related Content

What's hot (20)

Viewers also liked (11)

Similar to Model seminar shibata_100710 (20)

Model seminar shibata_100710

Editor's Notes