SVM
- 1. 厂痴惭勉强会(中山)
- 2. SVM(Support Vector Machine)とは ?? 教師あり学習の手法 –? 2クラスのパターン識別を行う手法 –? 未学習データに対して識別能力が高い(汎化能力) x2 ?? 線形二値分類器 ?? 非線形二値分類器 x1 2
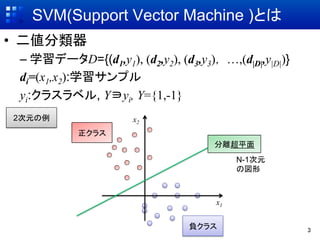
- 3. SVM(Support Vector Machine )とは ?? 二値分類器 –? 学習データD={(d1,y1), (d2,y2), (d3,y3), …,(d|D|,y|D|)} di=(x1,x2):学習サンプル yi:クラスラベル, Y?yi, Y={1,-1} 2次元の例 x2 正クラス 分離超平面 N-1次元 の図形 x1 負クラス 3
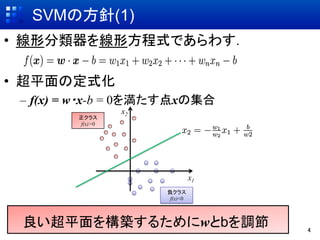
- 4. SVMの方針(1) ?? 線形分類器を線形方程式であらわす. ?? 超平面の定式化 –? f(x) = w?x-b = 0を満たす点xの集合 x2 正クラス f(x)>0 x1 負クラス f(x)<0 良い超平面を構築するためにwとbを調節 4
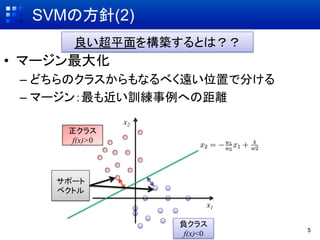
- 5. 厂痴惭の方针(2) 良い超平面を構築するとは?? ?? マージン最大化 –? どちらのクラスからもなるべく遠い位置で分ける –? マージン:最も近い訓練事例への距離 x2 正クラス f(x)>0 サポート ベクトル x1 負クラス 5 f(x)<0
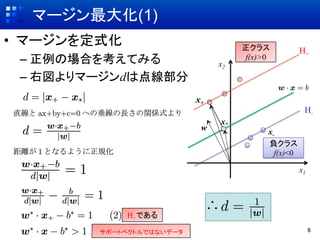
- 6. マージン最大化(1) ?? マージンを定式化 正クラス H+ –? 正例の場合を考えてみる x2 f(x)>0 –? 右図よりマージンdは点線部分 x+ H- x* w x- 負クラス f(x)<0 x1 H+である サポートベクトルではないデータ 6
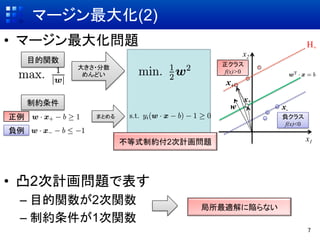
- 7. マージン最大化(2) ?? マージン最大化問題 H+ x2 目的関数 正クラス 大きさ?分数 f(x)>0 めんどい x+ 制約条件 x* w x- 正例 まとめる 負クラス f(x)<0 負例 不等式制約付2次計画問題 x1 ?? 凸2次計画問題で表す –? 目的関数が2次関数 局所最適解に陥らない –? 制約条件が1次関数 7
- 8. どうやって最適解を求めるか ?? 考えられる方法 –? x1で偏微分して0とおけば –? 必ずしもx2をx1で表現できるとは限らない ラグランジュの未定乗数法を使おう 8
- 9. ラグランジュの未定乗数法 ?? 解法 –? 変数λを導入し,ラグランジュ関数L(x,λ)を定義する –? 関数L(x,λ)のxに関する偏微分が0となり,かつ与えられ た制約が満たされる時,最適な解が得られる. 9
- 10. 计算例(等式制约) 停留点 10
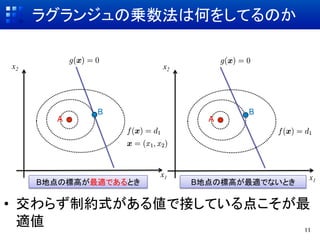
- 11. ラグランジュの乗数法は何をしてるのか x2 x2 B B A A x1 x1 B地点の標高が最適であるとき B地点の標高が最適でないとき ?? 交わらず制約式がある値で接している点こそが最 適値 11
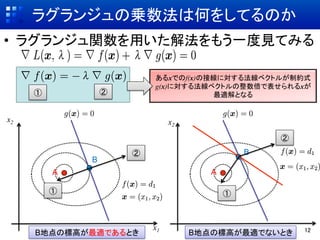
- 12. ラグランジュの乗数法は何をしてるのか ?? ラグランジュ関数を用いた解法をもう一度見てみる あるxでのf(x)の接線に対する法線ベクトルが制約式 g(x)に対する法線ベクトルの整数倍で表せられるxが ① ② 最適解となる x2 x2 ② ② B B A A ① ① x1 12 B地点の標高が最適であるとき B地点の標高が最適でないとき
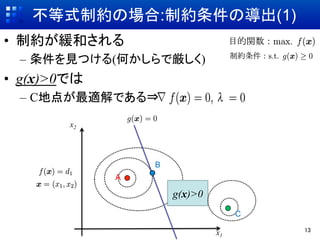
- 13. 不等式制約の場合:制約条件の導出(1) ?? 制約が緩和される –? 条件を見つける(何かしらで厳しく) ?? g(x)>0では –? C地点が最適解である? x2 B A g(x)>0 C x1 13
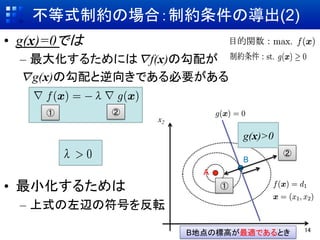
- 14. 不等式制約の場合:制約条件の導出(2) ?? g(x)=0では –? 最大化するためには?f(x)の勾配が ?g(x)の勾配と逆向きである必要がある ① ② x2 g(x)>0 ② B A ?? 最小化するためは ① –? 上式の左辺の符号を反転 B地点の標高が最適であるとき 14
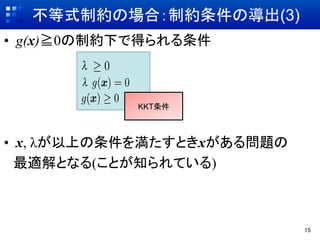
- 15. 不等式制約の場合:制約条件の導出(3) ?? g(x)≧0の制約下で得られる条件 KKT条件 ?? x, λが以上の条件を満たすときxがある問題の 最適解となる(ことが知られている) 15
- 16. 不等式制約:主問題と双対問題(1) ?? 先ほどの問題の不等式制約Ver 主問題 –? λに関する最小化問題に置き換える 双対問題 16
- 17. 不等式制約:主問題と双対問題(2) ?? λを変数とする関数で表せる ?? ラグランジュ関数に代入 ?? λに関する最適化問題(双対問題)に置き換えること で主問題を扱いやすくする. 制約条件は のみ 17
- 18. マージン最大化へ:主问题から双対问题 主問題 ?? ラグランジュ関数の導入 最小化なので- ?? (2)を元のラグランジュ関数に代入 18
- 19. マージン最大化へ:双対問題を解く ?? (3)を使って整理すると 双対問題 ?? αi以外は既知, ?? 制約条件を満たしラグランジュ関数が最大となるαi を求める 主問題から双対問題に持ってこれた! 19
- 20. Support Vectorと呼ばれる所以 ?? KKT条件から KKT条件 ?? xがサポートベクトルではない場合 ?? xがサポートベクトルである場合 αi≧0であるベクトルだけを考慮(支持:Support)する 20
- 21. SVMの計算例(1) ?? 学習データD={(d1,-1), (d2,-1),(d3,1)} d1=(0,1), d2=(1,1) d3=(2,1) x2 正クラス ?? まずは双対問題を解く 負クラス (0,1) (1,1) (2,1) x1 21
- 22. SVMの計算量(2) ?? 次はサポートベクトルのみ(α2, α3のみを考える) ?? 主問題へ 22
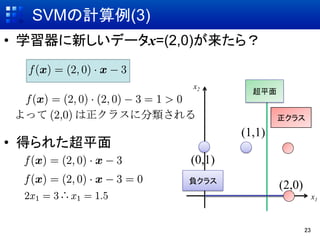
- 23. SVMの計算例(3) ?? 学習器に新しいデータx=(2,0)が来たら? x2 超平面 正クラス (1,1) ?? 得られた超平面 (0,1) 負クラス (2,0) x1 23