狠狠撸

SVM(Support Vector Machine)とは
? 教師あり学習の手法
– 2クラスのパターン識別を行う手法
– 未学習データに対して識別能力が高い(汎化能力)

x2
? 線形二値分類器

? 非線形二値分類器
x1

2

SVM(Support Vector Machine )とは
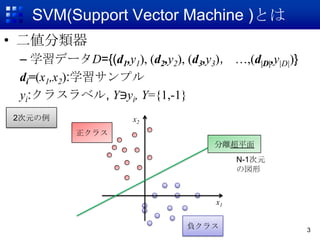
? 二値分類器
– 学習データD={(d1,y1), (d2,y2), (d3,y3)， …,(d|D|,y|D|)}
di=(x1,x2):学習サンプル
yi:クラスラベル, Y?yi, Y={1,-1}
2次元の例 x2
正クラス
分離超平面
N-1次元
の図形

x1

負クラス 3

SVMの方針(1)
? 線形分類器を線形方程式であらわす．

? 超平面の定式化
– f(x) = w?x-b = 0を満たす点xの集合
x2
正クラス
f(x)>0

x1
負クラス
f(x)<0

良い超平面を構築するためにwとbを調節 4

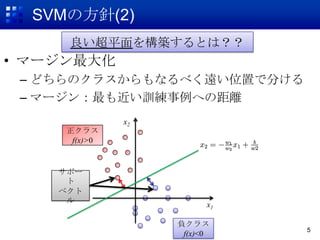
厂痴惭の方针(2)
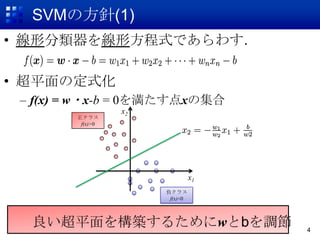
良い超平面を構築するとは？？
? マージン最大化
– どちらのクラスからもなるべく遠い位置で分ける
– マージン：最も近い訓練事例への距離
x2
正クラス
f(x)>0

サポー
ト
ベクト
ル
x1

負クラス
5
f(x)<0

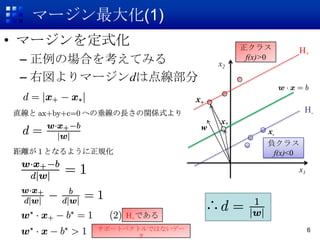
マージン最大化(1)
? マージンを定式化正クラス H+
– 正例の場合を考えてみる x2
f(x)>0

– 右図よりマージンdは点線部分
x+
H-
x*
w x-
負クラス
f(x)<0

x1

H+である
サポートベクトルではないデー 6
タ

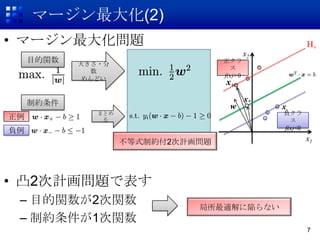
マージン最大化(2)
? マージン最大化問題 H+
x2
目的関数大きさ?分
正クラ
ス
数
f(x)>0
めんどい
x+

制約条件 x*
w x-
まとめ負クラ
正例るス
f(x)<0
負例
不等式制約付2次計画問題 x1

? 凸2次計画問題で表す
– 目的関数が2次関数局所最適解に陥らない
– 制約条件が1次関数
7

どうやって最適解を求めるか
? 考えられる方法

– x1で偏微分して0とおけば

– 必ずしもx2をx1で表現できるとは限らない

ラグランジュの未定乗数法を使
おう 8

ラグランジュの未定乗数法

? 解法
– 変数λを導入し，ラグランジュ関数L(x,λ)を定義する

– 関数L(x,λ)のxに関する偏微分が0となり，かつ与え
られた制約が満たされる時，最適な解が得られる．

9

计算例(等式制约)

停留点

10

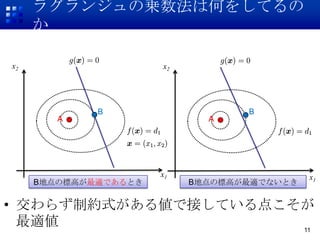
ラグランジュの乗数法は何をしてるの
か

x2 x2

B B
A A

x1 x1
B地点の標高が最適であるとき B地点の標高が最適でないとき

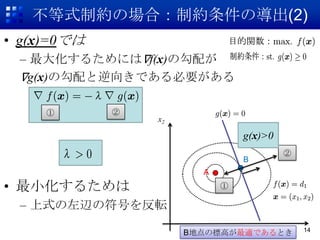
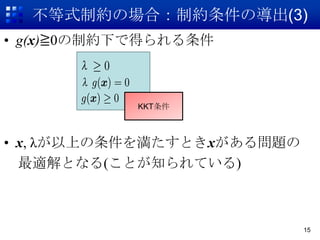
? 交わらず制約式がある値で接している点こそが
最適値 11

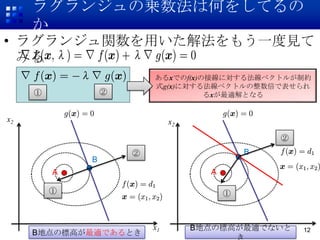
ラグランジュの乗数法は何をしてるの
か
? ラグランジュ関数を用いた解法をもう一度見て
みる
あるxでのf(x)の接線に対する法線ベクトルが制約
式g(x)に対する法線ベクトルの整数倍で表せられ
① ② るxが最適解となる

x2 x2

②
② B
B
A A

① ①

x1 B地点の標高が最適でないと 12
B地点の標高が最適であるとき

不等式制約の場合:制約条件の導出(1)
? 制約が緩和される
– 条件を見つける(何かしらで厳しく)
? g(x)>0では
– C地点が最適解である?

x2

B
A

g(x)>0
C

x1 13

不等式制約の場合：制約条件の導出(2)
? g(x)=0では
– 最大化するためには?f(x)の勾配が
?g(x)の勾配と逆向きである必要がある

① ②
x2

g(x)>0
②
B
A
? 最小化するためは ①

– 上式の左辺の符号を反転
14
B地点の標高が最適であるとき

不等式制約の場合：制約条件の導出(3)
? g(x)≧0の制約下で得られる条件

KKT条件

? x, λが以上の条件を満たすときxがある問題の
最適解となる(ことが知られている)

15

不等式制約：主問題と双対問題(1)
? 先ほどの問題の不等式制約Ver
主問題

– λに関する最小化問題に置き換える
双対問題

16

不等式制約：主問題と双対問題(2)
? λを変数とする関数で表せる

? ラグランジュ関数に代入

? λに関する最適化問題(双対問題)に置き換えるこ
とで主問題を扱いやすくする．

制約条件はのみ
17

マージン最大化へ:主問題から双対問
題
主問題

? ラグランジュ関数の導入
最小化なので－

? (2)を元のラグランジュ関数に代入

18

マージン最大化へ：双対問題を解く
? (3)を使って整理すると

双対問題

? αi以外は既知，
? 制約条件を満たしラグランジュ関数が最大とな
るαiを求める
主問題から双対問題に持ってこれた！

19

Support Vectorと呼ばれる所以
? KKT条件から

KKT条件
? xがサポートベクトルではない場合

? xがサポートベクトルである場合

αi≧0であるベクトルだけを考慮(支持:Support)する
20

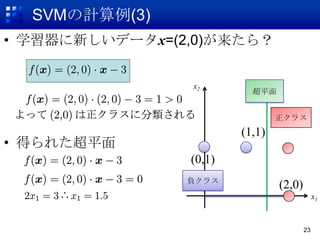
SVMの計算例(1)
? 学習データD={(d1,-1), (d2,-1),(d3,1)}
d1=(0,1), d2=(1,1) d3=(2,1) x2
正クラ
ス
? まずは双対問題を解く負クラス

(0,1) (1,1) (2,1)

x1

21

SVMの計算量(2)
? 次はサポートベクトルのみ(α2, α3のみを考える)

? 主問題へ

22

SVMの計算例(3)
? 学習器に新しいデータx=(2,0)が来たら？

x2
超平面

正クラス
(1,1)
? 得られた超平面
(0,1)
負クラス
(2,0)
x1

23

狠狠撸

SVM

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to SVM (20)

Recently uploaded (9)

SVM