04 hang ma tran
Download as ppt, pdf6 likes12,205 views
TĂ i liá»u trĂŹnh bĂ y vá» háșĄng ma tráșn trong ÄáșĄi sá» tuyáșżn tĂnh, vá»i cĂĄc phÆ°ÆĄng phĂĄp xĂĄc Äá»nh háșĄng thĂŽng qua ma tráșn hĂŹnh thang vĂ cĂĄc phĂ©p biáșżn Äá»i sÆĄ cáș„p. NĂł cĆ©ng ÄÆ°a ra vĂ dỄ cỄ thá» vá» cĂĄch tĂŹm háșĄng của cĂĄc ma tráșn khĂĄc nhau cĆ©ng nhÆ° cĂĄc bĂ i táșp Äá» thá»±c hĂ nh. Cuá»i cĂčng, tĂ i liá»u nháș„n máșĄnh táș§m quan trá»ng của viá»c biá»n luáșn háșĄng ma tráșn theo cĂĄc biáșżn sá».
1 of 22
Downloaded 27 times




![ÄáșĄi Sá» Tuyáșżn TĂnh Ă„
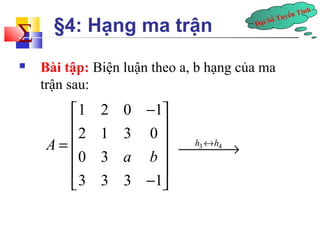
§4: HáșĄng ma tráșn
0 0 0 0
0 0 0 0
0 0 0 0
O
Ă© Ăč
= ĂȘ Ăș ĂȘ Ăș
ĂȘĂ« ĂșĂ»
2 [ ]
1 A = 0
24
13
0 0
0 0
A Ă© Ăč
= ĂȘ Ăș
Ă« Ă»](https://image.slidesharecdn.com/04hangmatran-141007084703-conversion-gate02/85/04-hang-ma-tran-6-320.jpg)












Ad
Recommended
05 hephuongtrinh
05 hephuongtrinhLĂȘ CĂŽng Tuáș„n Anh
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» phÆ°ÆĄng phĂĄp giáșŁi há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh trong ÄáșĄi sá» tuyáșżn tĂnh, Äáș·c biá»t sá» dỄng phÆ°ÆĄng phĂĄp Gauss. NĂł mĂŽ táșŁ cĂĄc phĂ©p biáșżn Äá»i tÆ°ÆĄng ÄÆ°ÆĄng trĂȘn há» phÆ°ÆĄng trĂŹnh vĂ Äiá»u kiá»n Äá» xĂĄc Äá»nh sá» nghiá»m của há». CĂĄc vĂ dỄ cỄ thá» ÄÆ°á»Łc ÄÆ°a ra nháș±m minh há»a quy trĂŹnh giáșŁi và ứng dỄng của cĂĄc phĂ©p biáșżn Äá»i nĂ y.02 dinh thuc
02 dinh thucNguyá»
n PhỄng
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» Äá»nh thức của ma tráșn vuĂŽng trong ÄáșĄi sá» tuyáșżn tĂnh, bao gá»m cĂĄch tĂnh Äá»nh thức cáș„p 2 vĂ 3 cĂčng vá»i cĂĄc vĂ dỄ cỄ thá». NĂł cĆ©ng tháșŁo luáșn vá» cĂĄc tĂnh cháș„t của Äá»nh thức, cĂĄc bĂ i táșp tĂnh Äá»nh thức vĂ những quy táșŻc biáșżn Äá»i giĂșp tĂnh toĂĄn Äá»nh thức hiá»u quáșŁ hÆĄn. NgoĂ i ra, tĂ i liá»u cuá»i cĂčng chứng minh má»t quy luáșt liĂȘn quan Äáșżn Äá»nh thức của tĂch hai ma tráșn.He phuong trinh (chuong 2)
He phuong trinh (chuong 2)Nguyá»
n PhỄng
Ìę
TĂ i liá»u nĂ y mĂŽ táșŁ cĂĄc há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh vĂ phÆ°ÆĄng phĂĄp giáșŁi của chĂșng, Äáș·c biá»t lĂ phÆ°ÆĄng phĂĄp Gauss. NĂł cung cáș„p nhiá»u vĂ dỄ vĂ bĂ i táșp liĂȘn quan Äáșżn há» phÆ°ÆĄng trĂŹnh, cĂčng vá»i cĂĄc quy táșŻc biáșżn Äá»i ma tráșn Äá» ÄÆ°a vá» dáșĄng hĂŹnh thang. CĂĄc tĂŹnh huá»ng vá» sá» lÆ°á»Łng nghiá»m của há» phÆ°ÆĄng trĂŹnh cĆ©ng ÄÆ°á»Łc tháșŁo luáșn.03 ma tran nghich dao
03 ma tran nghich daoNguyá»
n PhỄng
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» ma tráșn nghá»ch ÄáșŁo trong ÄáșĄi sá» tuyáșżn tĂnh, bao gá»m cĂĄc tĂnh cháș„t, vĂ dỄ cỄ thá» vĂ bĂ i táșp Äá» tĂŹm ma tráșn nghá»ch ÄáșŁo. NĂł cĆ©ng Äá» cáșp Äáșżn phÆ°ÆĄng phĂĄp Gauss Äá» tĂŹm ma tráșn nghá»ch ÄáșŁo vĂ cĂĄc biáșżn Äá»i sÆĄ cáș„p trĂȘn ma tráșn. Ná»i dung táșp trung vĂ o cĂĄc tĂnh toĂĄn vĂ cĂŽng thức liĂȘn quan Äáșżn ma tráșn vĂ há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh.Khong gian vecto (chuong 3)
Khong gian vecto (chuong 3)Nguyá»
n PhỄng
Ìę
ChÆ°ÆĄng 3 của tĂ i liá»u vá» ÄáșĄi sá» tuyáșżn tĂnh táșp trung vĂ o khĂŽng gian vector, sá»± Äá»c láșp vĂ phỄ thuá»c tuyáșżn tĂnh, háșĄng của má»t há» vector, vĂ cÆĄ sá» cĂčng sá» chiá»u của khĂŽng gian vector. NĂł trĂŹnh bĂ y cĂĄc khĂĄi niá»m cÆĄ báșŁn vĂ cĂĄc vĂ dỄ Äá» minh há»a cĂĄc tĂnh cháș„t của khĂŽng gian vector vĂ má»i quan há» giữa cĂĄc vectÆĄ. CĂĄc bĂ i táșp cĆ©ng ÄÆ°á»Łc ÄÆ°a ra Äá» kiá»m tra sá»± hiá»u biáșżt vá» cĂĄc khĂĄi niá»m nĂ y.Chuong03
Chuong03ChĂąu Thanh ChÆ°ÆĄng
Ìę
BĂ i giáșŁng phÆ°ÆĄng phĂĄp sá» chÆ°ÆĄng 3 trĂŹnh bĂ y cĂĄc phÆ°ÆĄng phĂĄp giáșŁi há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh, bao gá»m phÆ°ÆĄng phĂĄp Cramer vĂ phÆ°ÆĄng phĂĄp Gauss. PhÆ°ÆĄng phĂĄp Cramer cung cáș„p nghiá»m ÄĂșng nhÆ°ng yĂȘu cáș§u tĂnh toĂĄn nhiá»u Äá»nh thức, trong khi phÆ°ÆĄng phĂĄp Gauss ÄÆĄn giáșŁn hÆĄn vĂ cĂł thá» sá» dỄng sÆĄ Äá» Gauss Äá» háșĄn cháșż sai sĂłt. NgoĂ i ra, bĂ i giáșŁng cĆ©ng Äá» cáșp Äáșżn phÆ°ÆĄng phĂĄp Cholesky nhÆ° má»t cĂĄch giáșŁi há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh thĂŽng qua viá»c phĂąn tĂch ma tráșn.01 ma tran
01 ma tranNguyá»
n PhỄng
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» ma tráșn trong ÄáșĄi sá» tuyáșżn tĂnh, vá»i Äá»nh nghÄ©a vá» ma tráșn, cĂĄc loáșĄi ma tráșn Äáș·c biá»t nhÆ° ma tráșn khĂŽng, chĂ©o, ÄÆĄn vá», tam giĂĄc, cá»t, hĂ ng, vĂ cĂĄc phĂ©p toĂĄn trĂȘn ma tráșn nhÆ° cá»ng, nhĂąn vĂ tĂnh cháș„t của chĂșng. NĂł cĆ©ng Äá» cáșp Äáșżn ma tráșn chuyá»n vá», ma tráșn Äá»i xứng vĂ pháșŁn Äá»i xứng, cĂčng vá»i ứng dỄng của Äa thức trĂȘn ma tráșn. Cuá»i cĂčng, tĂ i liá»u cung cáș„p vĂ dỄ minh há»a cho cĂĄc khĂĄi niá»m ÄĂŁ nĂȘu.baÌng tra phĂąn phĂŽÌi chuĂąÌn
baÌng tra phĂąn phĂŽÌi chuĂąÌnRuc TrÆ°ÆĄng
Ìę
The document contains two tables of numbers. The first table lists values of the standard normal probability density function Ï(x) for values of x from 0 to 3.6. The second table lists values of the standard normal cumulative distribution function Ί(x) for values of x from 0 to 2.6. Both tables show the standard normal distribution, which is commonly used in statistics.TĂnh toĂĄn khoa há»c - ChÆ°ÆĄng 5: TĂnh gáș§n ÄĂșng ÄáșĄo hĂ m vĂ tĂch phĂąn
TĂnh toĂĄn khoa há»c - ChÆ°ÆĄng 5: TĂnh gáș§n ÄĂșng ÄáșĄo hĂ m vĂ tĂch phĂąnChien Dang
Ìę
ChÆ°ÆĄng 5 táșp trung vĂ o tĂnh gáș§n ÄĂșng cho ÄáșĄo hĂ m vĂ tĂch phĂąn, bao gá»m cĂĄc phÆ°ÆĄng phĂĄp sai phĂąn thuáșn, ngÆ°á»Łc vĂ trung tĂąm. Má»i phÆ°ÆĄng phĂĄp Äá»u ÄÆ°á»Łc giáșŁi thĂch vá»i cĂŽng thức, phĂąn tĂch sai sá» và ứng dỄng, Äá»ng thá»i cĂł bĂ i táșp minh há»a. NgoĂ i ra, chÆ°ÆĄng cĆ©ng Äá» cáșp Äáșżn cĂĄc phÆ°ÆĄng phĂĄp tĂnh gáș§n ÄĂșng tĂch phĂąn nhÆ° Newton-Cotes vĂ cĂŽng thức hĂŹnh thang.Chuong01
Chuong01ChĂąu Thanh ChÆ°ÆĄng
Ìę
TĂ i liá»u cung cáș„p kiáșżn thức vá» phÆ°ÆĄng phĂĄp sá», bao gá»m cĂĄc khĂĄi niá»m nhÆ° giĂĄ trá» gáș§n ÄĂșng, sai sá» tuyá»t Äá»i vĂ tÆ°ÆĄng Äá»i, cĆ©ng nhÆ° quy táșŻc tĂnh sai sá» trong cĂĄc phĂ©p toĂĄn. NĂł cĆ©ng tháșŁo luáșn vá» sá»± quy trĂČn sá» vĂ cĂĄch xĂĄc Äá»nh chữ sá» cĂł nghÄ©a trong cĂĄc giĂĄ trá» gáș§n ÄĂșng. ThĂŽng tin ÄÆ°á»Łc minh há»a qua nhiá»u vĂ dỄ cỄ thá» Äá» lĂ m rĂ” cĂĄc khĂĄi niá»m vĂ phÆ°ÆĄng phĂĄp tĂnh toĂĄn.PHÆŻÆ NG TRĂNH LÆŻá»ąNG GIĂC BáșŹC Má»T THEO SIN ,COS
PHÆŻÆ NG TRĂNH LÆŻá»ąNG GIĂC BáșŹC Má»T THEO SIN ,COSDANAMATH
Ìę
TĂ i liá»u nĂ y cung cáș„p kiáșżn thức vá» phÆ°ÆĄng trĂŹnh lÆ°á»Łng giĂĄc báșc má»t theo sin vĂ cos, bao gá»m cĂĄc cĂŽng thức vĂ phÆ°ÆĄng phĂĄp giáșŁi khĂĄc nhau. NĂł Äá» cáșp Äáșżn cĂĄc dáșĄng phÆ°ÆĄng trĂŹnh, cĂŽng thức háșĄ báșc, biáșżn Äá»i tĂch thĂ nh tá»ng, vĂ tá»ng thĂ nh tĂch vá»i ứng dỄng qua cĂĄc vĂ dỄ cỄ thá». Äá»ng thá»i, tĂ i liá»u cĆ©ng lÆ°u Ăœ vá» Äiá»u kiá»n vĂ dáș„u hiá»u sá» dỄng cĂĄc cĂŽng thức trong viá»c giáșŁi cĂĄc phÆ°ÆĄng trĂŹnh lÆ°á»Łng giĂĄc.Giao trinh Toan roi rac2
Giao trinh Toan roi rac2Ngo Hung Long
Ìę
ChÆ°ÆĄng 1 vá» ÄáșĄi sá» má»nh Äá» cung cáș„p kiáșżn thức cÆĄ báșŁn vá» má»nh Äá», chĂąn trá» vĂ cĂĄc phĂ©p toĂĄn má»nh Äá» nhÆ° phủ Äá»nh, há»i, tuyá»n vĂ kĂ©o theo. Ná»i dung chÆ°ÆĄng cĆ©ng bao gá»m cĂĄc ứng dỄng của logic trong láșp trĂŹnh vĂ Äá»i sá»ng hĂ ng ngĂ y. CĂĄc khĂĄi niá»m vĂ vĂ dỄ giĂșp sinh viĂȘn hiá»u vĂ ĂĄp dỄng ÄáșĄi sá» má»nh Äá» trong thá»±c tiá»
n.ÄáșĄi sá» tuyáșżn tĂnh 2 ( khĂŽng gian eculid )
ÄáșĄi sá» tuyáșżn tĂnh 2 ( khĂŽng gian eculid )Bui Loi
Ìę
TĂ i liá»u hÆ°á»ng dáș«n giáșŁi bĂ i táșp chÆ°ÆĄng 3 vá» khĂŽng gian Euclide, bao gá»m cĂĄc bĂ i táșp chứng minh tĂnh cháș„t của khĂŽng gian vector Euclide, tĂch vĂŽ hÆ°á»ng vĂ hÆ°á»ng dáș«n tĂŹm cÆĄ sá» trá»±c chuáș©n. CĂĄc bĂ i táșp yĂȘu cáș§u sinh viĂȘn thá»±c hiá»n cĂĄc chứng minh toĂĄn há»c Äá» xĂĄc Äá»nh Äiá»u kiá»n hoáș·c tĂnh cháș„t của cĂĄc khĂŽng gian vector trong cĂĄc bá»i cáșŁnh khĂĄc nhau. TĂ i liá»u cĆ©ng Äá» cáșp Äáșżn cĂĄc phÆ°ÆĄng phĂĄp nhÆ° phÆ°ÆĄng phĂĄp trá»±c giao hĂła Schmidt vĂ cĂĄc há» phÆ°ÆĄng trĂŹnh cáș§n thiáșżt Äá» xĂĄc Äá»nh cĂĄc vectÆĄ trong khĂŽng gian Euclide.PhĂąn tĂch má»t sá» thuáșt toĂĄn
PhĂąn tĂch má»t sá» thuáșt toĂĄnHá» Lợi
Ìę
TĂ i liá»u phĂąn tĂch cĂĄc thuáșt toĂĄn vĂ ká»č thuáșt liĂȘn quan Äáșżn sáșŻp xáșżp, bao gá»m sá» nghá»ch tháșż vĂ hĂ m sinh, cĆ©ng nhÆ° cĂĄc phÆ°ÆĄng phĂĄp sáșŻp xáșżp nhÆ° 'sáșŻp xáșżp báș±ng cĂĄch Äáșżm', 'sáșŻp xáșżp báș±ng cĂĄch chĂšn', vĂ 'quick sort'. CĂĄc Äá»nh lĂœ vĂ kÄ© thuáșt chứng minh vá» Äá» phức táșĄp của cĂĄc thuáșt toĂĄn ÄÆ°á»Łc trĂŹnh bĂ y, cho tháș„y ráș±ng cĂĄc thuáșt toĂĄn cĂł Äá» phức táșĄp khĂĄc nhau trong cĂĄc trÆ°á»ng hợp tá»t nháș„t vĂ xáș„u nháș„t. Cuá»i cĂčng, tĂ i liá»u ÄÆ°a ra má»t sá» bĂ i táșp vá» thuáșt toĂĄn sáșŻp xáșżp vĂ tĂŹm kiáșżm.DĂŁy sá» vĂ giá»i háșĄn
DĂŁy sá» vĂ giá»i háșĄnChĂ ng Trai CĂŽ ÄÆĄn
Ìę
TĂ i liá»u nĂ y trĂŹnh bĂ y những phÆ°ÆĄng phĂĄp vĂ lĂœ thuyáșżt vá» dĂŁy sá» cĂčng vá»i cĂĄc bĂ i toĂĄn liĂȘn quan, nháș±m ÄĂłng gĂłp cho lÄ©nh vá»±c toĂĄn há»c nĂ y. Ná»i dung khĂŽng chá» bao gá»m Äá»nh nghÄ©a vĂ Äá»nh lĂœ cÆĄ báșŁn mĂ cĂČn cĂĄc phÆ°ÆĄng phĂĄp giáșŁi, Äá»nh lĂœ vá» giá»i háșĄn vĂ sai phĂąn. TĂĄc giáșŁ kĂȘu gá»i sá»± gĂłp Ăœ từ Äá»c giáșŁ Äá» hoĂ n thiá»n tĂ i liá»u.Bo de toan roi rac (on thi cao hoc khmt)
Bo de toan roi rac (on thi cao hoc khmt)lieu_lamlam
Ìę
TĂ i liá»u hÆ°á»ng dáș«n sinh viĂȘn ngĂ nh cĂŽng nghá» thĂŽng tin vĂ thĂ sinh luyá»n thi cao há»c ngĂ nh khoa há»c mĂĄy tĂnh vá» cĂĄc bĂ i toĂĄn trong toĂĄn rá»i ráșĄc. NĂł bao gá»m cĂĄc váș„n Äá» từ Äáșżm sá» lÆ°á»Łng kĂœ tá»± vĂ xĂąu nhá» phĂąn Äáșżn bĂ i toĂĄn liĂȘn quan Äáșżn biá»n sá» xe. TĂ i liá»u cung cáș„p cĂŽng thức vĂ phÆ°ÆĄng phĂĄp giáșŁi, giĂșp ngÆ°á»i há»c náșŻm vững cĂĄc nguyĂȘn lĂœ cÆĄ báșŁn trong toĂĄn rá»i ráșĄc.PHĂN PHá»I CHUáșšN HAI BIáșŸN _ BIVARIATE NORMAL DISTRIBUTION
PHĂN PHá»I CHUáșšN HAI BIáșŸN _ BIVARIATE NORMAL DISTRIBUTIONSoM
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» phĂąn phá»i chuáș©n hai biáșżn (bivariate normal distribution) vĂ chứng minh ráș±ng hai Äá»nh nghÄ©a của nĂł lĂ tÆ°ÆĄng ÄÆ°ÆĄng. NĂł cĆ©ng tháșŁo luáșn vá» cĂĄc khĂĄi niá»m nhÆ° hĂ m máșt Äá» xĂĄc suáș„t káșżt hợp, hĂ m phĂąn phá»i tĂch lĆ©y vĂ cĂĄc tĂnh cháș„t, Äá»nh lĂœ liĂȘn quan Äáșżn biáșżn ngáș«u nhiĂȘn Äá»c láșp. Cuá»i cĂčng, tĂ i liá»u cung cáș„p má»t sá» káșżt quáșŁ nghiĂȘn cứu vá» biáșżn ngáș«u nhiĂȘn liĂȘn tỄc vĂ cĂĄc chủ Äá» liĂȘn quan Äáșżn kỳ vá»ng, phÆ°ÆĄng sai vĂ hĂ m máșt Äá» xĂĄc suáș„t Äiá»u kiá»n.CĂŽng thức Váșt lĂœ ÄáșĄi cÆ°ÆĄng III
CĂŽng thức Váșt lĂœ ÄáșĄi cÆ°ÆĄng IIIVĆ© LĂąm
Ìę
TĂ i liá»u trĂŹnh bĂ y cĂŽng thức vĂ Äiá»u kiá»n giao thoa ĂĄnh sĂĄng, bao gá»m cĂĄc cĂŽng thức liĂȘn quan Äáșżn cá»±c ÄáșĄi vĂ cá»±c tiá»u giao thoa, cĆ©ng nhÆ° cĂĄc bĂ i toĂĄn vá» giao thoa vĂ nhiá»
u xáșĄ ĂĄnh sĂĄng. NĂł giáșŁi thĂch cĂĄc hiá»n tÆ°á»Łng liĂȘn quan Äáșżn viá»c sá» dỄng báșŁn má»ng, vá» trĂ vĂąn sĂĄng tá»i vĂ cĂĄc phÆ°ÆĄng phĂĄp nhiá»
u xáșĄ khĂĄc nhau. TĂ i liá»u cĆ©ng Äá» cáșp Äáșżn phĂąn cá»±c ĂĄnh sĂĄng vĂ quang há»c lÆ°á»Łng tá», trong ÄĂł cĂł khĂĄi niá»m vá» váșt Äen tuyá»t Äá»i.XĂąy dá»±ng cÆĄ sá» dữ liá»u trong quáșŁn lĂœ nhĂąn sá»±
XĂąy dá»±ng cÆĄ sá» dữ liá»u trong quáșŁn lĂœ nhĂąn sá»±AskSock NgĂŽ Quang ÄáșĄo
Ìę
TĂ i liá»u trĂŹnh bĂ y cĂĄch xĂąy dá»±ng cÆĄ sá» dữ liá»u trong quáșŁn lĂœ nhĂąn sá»±, bao gá»m tá»ng quan vá» há» thá»ng quáșŁn lĂœ, cĂĄc chức nÄng, nhiá»m vỄ vĂ yĂȘu cáș§u của há» thá»ng. NĂł cĆ©ng Äá» cáșp Äáșżn viá»c thiáșżt káșż mĂŽ hĂŹnh cÆĄ sá» dữ liá»u, phĂąn tĂch cĂĄc báșŁng dữ liá»u cáș§n thiáșżt vĂ thá»±c hiá»n chuáș©n hĂła. Cuá»i cĂčng, tĂ i liá»u giá»i thiá»u cĂĄch sá» dỄng Microsoft Access vĂ SQL Äá» quáșŁn lĂœ vĂ truy xuáș„t dữ liá»u hiá»u quáșŁ.BĂ i táșp sá» phức
BĂ i táșp sá» phứcphuonganhtran1303
Ìę
Sá» phức cĂł dáșĄng a + bi, trong ÄĂł a vĂ b lĂ sá» thá»±c, vĂ i lĂ ÄÆĄn vá» áșŁo vá»i iÂČ = -1. CĂĄc phĂ©p toĂĄn nhÆ° cá»ng, trừ, nhĂąn vĂ chia sá» phức, cĆ©ng nhÆ° biá»u diá»
n hĂŹnh há»c trĂȘn máș·t pháșłng tá»a Äá», Äá»u ÄÆ°á»Łc Äá»nh nghÄ©a rĂ” rĂ ng trong tĂ i liá»u. NgoĂ i ra, tĂ i liá»u cĂČn Äá» cáșp Äáșżn dáșĄng lÆ°á»Łng giĂĄc của sá» phức vĂ cĂĄc phÆ°ÆĄng phĂĄp giáșŁi toĂĄn cÆĄ báșŁn liĂȘn quan Äáșżn sá» phức.Luáșn vÄn: Biáșżn Äá»i Laplace vĂ má»t sỠứng dỄng, HAY, 9Ä
Luáșn vÄn: Biáșżn Äá»i Laplace vĂ má»t sỠứng dỄng, HAY, 9ÄDá»ch vỄ viáșżt bĂ i trá»n gĂłi ZALO: 0909232620
Ìę
Luáșn vÄn tháșĄc sÄ© nĂ y nghiĂȘn cứu vá» biáșżn Äá»i Laplace, má»t phĂ©p biáșżn Äá»i tĂch phĂąn quan trá»ng, vĂ cĂĄc ứng dỄng của nĂł trong giáșŁi quyáșżt cĂĄc phÆ°ÆĄng trĂŹnh vi phĂąn vĂ bĂ i toĂĄn liĂȘn quan. TĂ i liá»u trĂŹnh bĂ y lĂœ thuyáșżt cÆĄ báșŁn, tĂnh cháș„t vĂ cĂĄc phÆ°ÆĄng phĂĄp tĂŹm biáșżn Äá»i Laplace ngÆ°á»Łc, cĂčng vá»i cĂĄc ứng dỄng trong váșt lĂœ vĂ khoa há»c ká»č thuáșt. NghiĂȘn cứu cĆ©ng bao gá»m cĂĄc Äiá»u kiá»n tá»n táșĄi vĂ cĂĄc vĂ dỄ cỄ thá» vá» biáșżn Äá»i Laplace.BĂ i giáșŁng xĂĄc suáș„t thá»ng kĂȘ
BĂ i giáșŁng xĂĄc suáș„t thá»ng kĂȘHá»c Huỳnh BĂĄ
Ìę
TĂ i liá»u cung cáș„p kiáșżn thức cÆĄ báșŁn vá» xĂĄc suáș„t vĂ thá»ng kĂȘ, báșŻt Äáș§u từ cĂĄc khĂĄi niá»m vá» hiá»n tÆ°á»Łng ngáș«u nhiĂȘn, biáșżn cá», vĂ cĂĄc phĂ©p toĂĄn liĂȘn quan Äáșżn biáșżn cá». NĂł giáșŁi thĂch cĂĄch xĂĄc Äá»nh xĂĄc suáș„t của cĂĄc biáșżn cá» thĂŽng qua cĂĄc phÆ°ÆĄng phĂĄp cá» Äiá»n vĂ thá»ng kĂȘ, cĆ©ng nhÆ° cĂĄc khĂĄi niá»m liĂȘn quan Äáșżn báșŁng phĂąn phá»i táș§n sá». NgoĂ i ra, tĂ i liá»u cĆ©ng Äá» cáșp Äáșżn quy trĂŹnh thu tháșp vĂ phĂąn tĂch dữ liá»u trong nghiĂȘn cứu thá»ng kĂȘ.Ma tráșn - Äá»nh thức vĂ cĂĄc ứng dỄng trong kinh táșż
Ma tráșn - Äá»nh thức vĂ cĂĄc ứng dỄng trong kinh táșżngTonH1
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» ma tráșn vĂ cĂĄc phĂ©p toĂĄn tuyáșżn tĂnh trong bá» mĂŽn toĂĄn kinh táșż vĂ khoa há»c dữ liá»u, bao gá»m cĂĄc khĂĄi niá»m cÆĄ báșŁn vá» ma tráșn, cĂĄc dáșĄng ma tráșn nhÆ° ma tráșn vuĂŽng, tam giĂĄc, ÄÆ°á»ng chĂ©o vĂ ÄÆĄn vá». NgoĂ i ra, tĂ i liá»u cĂČn nĂȘu rĂ” cĂĄc phĂ©p toĂĄn tuyáșżn tĂnh, vĂ dỄ thá»±c táșż vĂ tĂnh cháș„t của phĂ©p toĂĄn Äá»i vá»i cĂĄc ma tráșn. Cuá»i cĂčng, tĂ i liá»u cung cáș„p cĂĄc phÆ°ÆĄng phĂĄp tĂnh Äá»nh thức vĂ nhĂąn ma tráșn.PhÆ°ÆĄng phĂĄp runge kutta giáșŁi gáș§n ÄĂșng há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá»
PhÆ°ÆĄng phĂĄp runge kutta giáșŁi gáș§n ÄĂșng há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá»Khu Tiáșżn
Ìę
Luáșn vÄn của VĆ© Huy BĂŹnh trĂŹnh bĂ y vá» phÆ°ÆĄng phĂĄp Runge-Kutta Äá» giáșŁi gáș§n ÄĂșng há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá», má»t lÄ©nh vá»±c cĂł nhiá»u ứng dỄng thá»±c tiá»
n trong cĂĄc ngĂ nh khoa há»c vĂ ká»č thuáșt. TĂĄc giáșŁ ÄĂŁ chia luáșn vÄn thĂ nh ba chÆ°ÆĄng, gá»m cĂĄc khĂĄi niá»m cÆĄ báșŁn vá» há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá», phÆ°ÆĄng phĂĄp Runge-Kutta, và ứng dỄng của phÆ°ÆĄng phĂĄp nĂ y qua cĂĄc vĂ dỄ cỄ thá». Luáșn vÄn ÄÆ°á»Łc hoĂ n thĂ nh dÆ°á»i sá»± hÆ°á»ng dáș«n của TS. Nguyá»
n VÄn Minh táșĄi ÄáșĄi há»c ThĂĄi NguyĂȘn vĂ o nÄm 2012.Äáș I Sá» TUYáșŸN TĂNH.pdf
Äáș I Sá» TUYáșŸN TĂNH.pdf0058NguynVHongSn
Ìę
TĂ i liá»u chủ yáșżu Äá» cáșp Äáșżn cĂĄc khĂĄi niá»m vĂ phĂ©p toĂĄn liĂȘn quan Äáșżn ma tráșn, bao gá»m Äá»nh thức, há» phÆ°ÆĄng trĂŹnh, khĂŽng gian vector vĂ ĂĄnh xáșĄ tuyáșżn tĂnh. NĂł bao gá»m cĂĄc ná»i dung nhÆ° phĂ©p cá»ng, trừ, nhĂąn ma tráșn vĂ lĆ©y thừa của ma tráșn, cĆ©ng nhÆ° cĂĄc biáșżn Äá»i sÆĄ cáș„p trĂȘn ma tráșn. TĂ i liá»u cĂČn giáșŁi thĂch chi tiáșżt vá» cĂĄc loáșĄi ma tráșn nhÆ° ma tráșn khĂŽng, ma tráșn kháșŁ nghá»ch, vĂ cĂĄc tĂnh cháș„t của chĂșng.Luáșn vÄn: GiáșŁi bĂ i toĂĄn Dirichlet Äá»i vá»i phÆ°ÆĄng trĂŹnh Elliptic, 9Ä
Luáșn vÄn: GiáșŁi bĂ i toĂĄn Dirichlet Äá»i vá»i phÆ°ÆĄng trĂŹnh Elliptic, 9ÄDá»ch vỄ viáșżt bĂ i trá»n gĂłi ZALO 0917193864
Ìę
Luáșn vÄn tháșĄc sá»č của BĂči Thá» Oanh nghiĂȘn cứu vá» phÆ°ÆĄng phĂĄp nghiá»m trĂȘn nghiá»m dÆ°á»i Äá» giáșŁi bĂ i toĂĄn Dirichlet cho phÆ°ÆĄng trĂŹnh elliptic. TĂ i liá»u bao gá»m ba chÆ°ÆĄng, trong ÄĂł trĂŹnh bĂ y cĂĄc kiáșżn thức cÆĄ báșŁn vá» khĂŽng gian Sobolev, toĂĄn tá» vi phĂąn elliptic và ứng dỄng của phÆ°ÆĄng phĂĄp láș·p ÄÆĄn Äiá»u. BĂȘn cáșĄnh ÄĂł, luáșn vÄn cĆ©ng cung cáș„p chứng minh vĂ vĂ dỄ ĂĄp dỄng nháș±m phĂĄt triá»n lĂœ thuyáșżt vĂ phÆ°ÆĄng phĂĄp liĂȘn quan Äáșżn bĂ i toĂĄn Dirichlet ná»a tuyáșżn tĂnh.Bai7 khai trien_taylor
Bai7 khai trien_taylorljmonking
Ìę
TĂ i liá»u trĂŹnh bĂ y cĂŽng thức khai triá»n Taylor vĂ cĂĄc pháș§n dÆ° Lagrange cĆ©ng nhÆ° Peano, cĂčng vá»i vĂ dỄ minh há»a cỄ thá» cho viá»c khai triá»n cĂĄc hĂ m sá» nhÆ° sin, tan vĂ cĂĄc Äa thức. TĂ i liá»u giáșŁi thĂch Ăœ nghÄ©a của khai triá»n Taylor trong viá»c ÄÆĄn giáșŁn hĂła tĂnh toĂĄn vá»i cĂĄc hĂ m phức táșĄp thĂŽng qua cĂĄc Äa thức. NĂł cĆ©ng Äá» cáșp Äáșżn cĂĄc phÆ°ÆĄng phĂĄp khai triá»n Äáșżn cáș„p Äá» khĂĄc nhau vĂ cĂĄch ĂĄp dỄng chĂșng trong cĂĄc trÆ°á»ng hợp cỄ thá».04 hangmatran
04 hangmatranLĂȘ CĂŽng Tuáș„n Anh
Ìę
TĂ i liá»u trĂŹnh bĂ y khĂĄi niá»m 'háșĄng ma tráșn' trong ÄáșĄi sá» tuyáșżn tĂnh, giĂșp xĂĄc Äá»nh cĂĄc trÆ°á»ng hợp của há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh, bao gá»m há» vĂŽ nghiá»m, cĂł nghiá»m duy nháș„t hoáș·c cĂł vĂŽ sá» nghiá»m. HáșĄng ma tráșn ÄÆ°á»Łc so sĂĄnh giữa ma tráșn há» sá» vĂ ma tráșn há» sá» má» rá»ng Äá» xĂĄc Äá»nh loáșĄi nghiá»m của há» phÆ°ÆĄng trĂŹnh. TĂ i liá»u cung cáș„p cĂĄc vĂ dỄ vĂ bĂ i táșp vá» viá»c xĂĄc Äá»nh háșĄng ma tráșn.01 matran
01 matranLĂȘ CĂŽng Tuáș„n Anh
Ìę
TĂ i liá»u cung cáș„p kiáșżn thức cÆĄ báșŁn vá» ma tráșn vĂ cĂĄc loáșĄi ma tráșn trong ÄáșĄi sá» tuyáșżn tĂnh, bao gá»m ma tráșn khĂŽng, ma tráșn vuĂŽng, ma tráșn chĂ©o, vĂ cĂĄc ma tráșn Äáș·c biá»t khĂĄc. NgoĂ i ra, tĂ i liá»u cĂČn trĂŹnh bĂ y cĂĄc phĂ©p toĂĄn trĂȘn ma tráșn nhÆ° phĂ©p cá»ng vĂ phĂ©p nhĂąn vá»i má»t sá». CĂĄc vĂ dỄ cỄ thá» ÄÆ°á»Łc ÄÆ°a ra Äá» minh há»a cho từng loáșĄi ma tráșn vĂ phĂ©p toĂĄn.More Related Content
What's hot (20)
TĂnh toĂĄn khoa há»c - ChÆ°ÆĄng 5: TĂnh gáș§n ÄĂșng ÄáșĄo hĂ m vĂ tĂch phĂąn
TĂnh toĂĄn khoa há»c - ChÆ°ÆĄng 5: TĂnh gáș§n ÄĂșng ÄáșĄo hĂ m vĂ tĂch phĂąnChien Dang
Ìę
ChÆ°ÆĄng 5 táșp trung vĂ o tĂnh gáș§n ÄĂșng cho ÄáșĄo hĂ m vĂ tĂch phĂąn, bao gá»m cĂĄc phÆ°ÆĄng phĂĄp sai phĂąn thuáșn, ngÆ°á»Łc vĂ trung tĂąm. Má»i phÆ°ÆĄng phĂĄp Äá»u ÄÆ°á»Łc giáșŁi thĂch vá»i cĂŽng thức, phĂąn tĂch sai sá» và ứng dỄng, Äá»ng thá»i cĂł bĂ i táșp minh há»a. NgoĂ i ra, chÆ°ÆĄng cĆ©ng Äá» cáșp Äáșżn cĂĄc phÆ°ÆĄng phĂĄp tĂnh gáș§n ÄĂșng tĂch phĂąn nhÆ° Newton-Cotes vĂ cĂŽng thức hĂŹnh thang.Chuong01
Chuong01ChĂąu Thanh ChÆ°ÆĄng
Ìę
TĂ i liá»u cung cáș„p kiáșżn thức vá» phÆ°ÆĄng phĂĄp sá», bao gá»m cĂĄc khĂĄi niá»m nhÆ° giĂĄ trá» gáș§n ÄĂșng, sai sá» tuyá»t Äá»i vĂ tÆ°ÆĄng Äá»i, cĆ©ng nhÆ° quy táșŻc tĂnh sai sá» trong cĂĄc phĂ©p toĂĄn. NĂł cĆ©ng tháșŁo luáșn vá» sá»± quy trĂČn sá» vĂ cĂĄch xĂĄc Äá»nh chữ sá» cĂł nghÄ©a trong cĂĄc giĂĄ trá» gáș§n ÄĂșng. ThĂŽng tin ÄÆ°á»Łc minh há»a qua nhiá»u vĂ dỄ cỄ thá» Äá» lĂ m rĂ” cĂĄc khĂĄi niá»m vĂ phÆ°ÆĄng phĂĄp tĂnh toĂĄn.PHÆŻÆ NG TRĂNH LÆŻá»ąNG GIĂC BáșŹC Má»T THEO SIN ,COS
PHÆŻÆ NG TRĂNH LÆŻá»ąNG GIĂC BáșŹC Má»T THEO SIN ,COSDANAMATH
Ìę
TĂ i liá»u nĂ y cung cáș„p kiáșżn thức vá» phÆ°ÆĄng trĂŹnh lÆ°á»Łng giĂĄc báșc má»t theo sin vĂ cos, bao gá»m cĂĄc cĂŽng thức vĂ phÆ°ÆĄng phĂĄp giáșŁi khĂĄc nhau. NĂł Äá» cáșp Äáșżn cĂĄc dáșĄng phÆ°ÆĄng trĂŹnh, cĂŽng thức háșĄ báșc, biáșżn Äá»i tĂch thĂ nh tá»ng, vĂ tá»ng thĂ nh tĂch vá»i ứng dỄng qua cĂĄc vĂ dỄ cỄ thá». Äá»ng thá»i, tĂ i liá»u cĆ©ng lÆ°u Ăœ vá» Äiá»u kiá»n vĂ dáș„u hiá»u sá» dỄng cĂĄc cĂŽng thức trong viá»c giáșŁi cĂĄc phÆ°ÆĄng trĂŹnh lÆ°á»Łng giĂĄc.Giao trinh Toan roi rac2
Giao trinh Toan roi rac2Ngo Hung Long
Ìę
ChÆ°ÆĄng 1 vá» ÄáșĄi sá» má»nh Äá» cung cáș„p kiáșżn thức cÆĄ báșŁn vá» má»nh Äá», chĂąn trá» vĂ cĂĄc phĂ©p toĂĄn má»nh Äá» nhÆ° phủ Äá»nh, há»i, tuyá»n vĂ kĂ©o theo. Ná»i dung chÆ°ÆĄng cĆ©ng bao gá»m cĂĄc ứng dỄng của logic trong láșp trĂŹnh vĂ Äá»i sá»ng hĂ ng ngĂ y. CĂĄc khĂĄi niá»m vĂ vĂ dỄ giĂșp sinh viĂȘn hiá»u vĂ ĂĄp dỄng ÄáșĄi sá» má»nh Äá» trong thá»±c tiá»
n.ÄáșĄi sá» tuyáșżn tĂnh 2 ( khĂŽng gian eculid )
ÄáșĄi sá» tuyáșżn tĂnh 2 ( khĂŽng gian eculid )Bui Loi
Ìę
TĂ i liá»u hÆ°á»ng dáș«n giáșŁi bĂ i táșp chÆ°ÆĄng 3 vá» khĂŽng gian Euclide, bao gá»m cĂĄc bĂ i táșp chứng minh tĂnh cháș„t của khĂŽng gian vector Euclide, tĂch vĂŽ hÆ°á»ng vĂ hÆ°á»ng dáș«n tĂŹm cÆĄ sá» trá»±c chuáș©n. CĂĄc bĂ i táșp yĂȘu cáș§u sinh viĂȘn thá»±c hiá»n cĂĄc chứng minh toĂĄn há»c Äá» xĂĄc Äá»nh Äiá»u kiá»n hoáș·c tĂnh cháș„t của cĂĄc khĂŽng gian vector trong cĂĄc bá»i cáșŁnh khĂĄc nhau. TĂ i liá»u cĆ©ng Äá» cáșp Äáșżn cĂĄc phÆ°ÆĄng phĂĄp nhÆ° phÆ°ÆĄng phĂĄp trá»±c giao hĂła Schmidt vĂ cĂĄc há» phÆ°ÆĄng trĂŹnh cáș§n thiáșżt Äá» xĂĄc Äá»nh cĂĄc vectÆĄ trong khĂŽng gian Euclide.PhĂąn tĂch má»t sá» thuáșt toĂĄn
PhĂąn tĂch má»t sá» thuáșt toĂĄnHá» Lợi
Ìę
TĂ i liá»u phĂąn tĂch cĂĄc thuáșt toĂĄn vĂ ká»č thuáșt liĂȘn quan Äáșżn sáșŻp xáșżp, bao gá»m sá» nghá»ch tháșż vĂ hĂ m sinh, cĆ©ng nhÆ° cĂĄc phÆ°ÆĄng phĂĄp sáșŻp xáșżp nhÆ° 'sáșŻp xáșżp báș±ng cĂĄch Äáșżm', 'sáșŻp xáșżp báș±ng cĂĄch chĂšn', vĂ 'quick sort'. CĂĄc Äá»nh lĂœ vĂ kÄ© thuáșt chứng minh vá» Äá» phức táșĄp của cĂĄc thuáșt toĂĄn ÄÆ°á»Łc trĂŹnh bĂ y, cho tháș„y ráș±ng cĂĄc thuáșt toĂĄn cĂł Äá» phức táșĄp khĂĄc nhau trong cĂĄc trÆ°á»ng hợp tá»t nháș„t vĂ xáș„u nháș„t. Cuá»i cĂčng, tĂ i liá»u ÄÆ°a ra má»t sá» bĂ i táșp vá» thuáșt toĂĄn sáșŻp xáșżp vĂ tĂŹm kiáșżm.DĂŁy sá» vĂ giá»i háșĄn
DĂŁy sá» vĂ giá»i háșĄnChĂ ng Trai CĂŽ ÄÆĄn
Ìę
TĂ i liá»u nĂ y trĂŹnh bĂ y những phÆ°ÆĄng phĂĄp vĂ lĂœ thuyáșżt vá» dĂŁy sá» cĂčng vá»i cĂĄc bĂ i toĂĄn liĂȘn quan, nháș±m ÄĂłng gĂłp cho lÄ©nh vá»±c toĂĄn há»c nĂ y. Ná»i dung khĂŽng chá» bao gá»m Äá»nh nghÄ©a vĂ Äá»nh lĂœ cÆĄ báșŁn mĂ cĂČn cĂĄc phÆ°ÆĄng phĂĄp giáșŁi, Äá»nh lĂœ vá» giá»i háșĄn vĂ sai phĂąn. TĂĄc giáșŁ kĂȘu gá»i sá»± gĂłp Ăœ từ Äá»c giáșŁ Äá» hoĂ n thiá»n tĂ i liá»u.Bo de toan roi rac (on thi cao hoc khmt)
Bo de toan roi rac (on thi cao hoc khmt)lieu_lamlam
Ìę
TĂ i liá»u hÆ°á»ng dáș«n sinh viĂȘn ngĂ nh cĂŽng nghá» thĂŽng tin vĂ thĂ sinh luyá»n thi cao há»c ngĂ nh khoa há»c mĂĄy tĂnh vá» cĂĄc bĂ i toĂĄn trong toĂĄn rá»i ráșĄc. NĂł bao gá»m cĂĄc váș„n Äá» từ Äáșżm sá» lÆ°á»Łng kĂœ tá»± vĂ xĂąu nhá» phĂąn Äáșżn bĂ i toĂĄn liĂȘn quan Äáșżn biá»n sá» xe. TĂ i liá»u cung cáș„p cĂŽng thức vĂ phÆ°ÆĄng phĂĄp giáșŁi, giĂșp ngÆ°á»i há»c náșŻm vững cĂĄc nguyĂȘn lĂœ cÆĄ báșŁn trong toĂĄn rá»i ráșĄc.PHĂN PHá»I CHUáșšN HAI BIáșŸN _ BIVARIATE NORMAL DISTRIBUTION
PHĂN PHá»I CHUáșšN HAI BIáșŸN _ BIVARIATE NORMAL DISTRIBUTIONSoM
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» phĂąn phá»i chuáș©n hai biáșżn (bivariate normal distribution) vĂ chứng minh ráș±ng hai Äá»nh nghÄ©a của nĂł lĂ tÆ°ÆĄng ÄÆ°ÆĄng. NĂł cĆ©ng tháșŁo luáșn vá» cĂĄc khĂĄi niá»m nhÆ° hĂ m máșt Äá» xĂĄc suáș„t káșżt hợp, hĂ m phĂąn phá»i tĂch lĆ©y vĂ cĂĄc tĂnh cháș„t, Äá»nh lĂœ liĂȘn quan Äáșżn biáșżn ngáș«u nhiĂȘn Äá»c láșp. Cuá»i cĂčng, tĂ i liá»u cung cáș„p má»t sá» káșżt quáșŁ nghiĂȘn cứu vá» biáșżn ngáș«u nhiĂȘn liĂȘn tỄc vĂ cĂĄc chủ Äá» liĂȘn quan Äáșżn kỳ vá»ng, phÆ°ÆĄng sai vĂ hĂ m máșt Äá» xĂĄc suáș„t Äiá»u kiá»n.CĂŽng thức Váșt lĂœ ÄáșĄi cÆ°ÆĄng III
CĂŽng thức Váșt lĂœ ÄáșĄi cÆ°ÆĄng IIIVĆ© LĂąm
Ìę
TĂ i liá»u trĂŹnh bĂ y cĂŽng thức vĂ Äiá»u kiá»n giao thoa ĂĄnh sĂĄng, bao gá»m cĂĄc cĂŽng thức liĂȘn quan Äáșżn cá»±c ÄáșĄi vĂ cá»±c tiá»u giao thoa, cĆ©ng nhÆ° cĂĄc bĂ i toĂĄn vá» giao thoa vĂ nhiá»
u xáșĄ ĂĄnh sĂĄng. NĂł giáșŁi thĂch cĂĄc hiá»n tÆ°á»Łng liĂȘn quan Äáșżn viá»c sá» dỄng báșŁn má»ng, vá» trĂ vĂąn sĂĄng tá»i vĂ cĂĄc phÆ°ÆĄng phĂĄp nhiá»
u xáșĄ khĂĄc nhau. TĂ i liá»u cĆ©ng Äá» cáșp Äáșżn phĂąn cá»±c ĂĄnh sĂĄng vĂ quang há»c lÆ°á»Łng tá», trong ÄĂł cĂł khĂĄi niá»m vá» váșt Äen tuyá»t Äá»i.XĂąy dá»±ng cÆĄ sá» dữ liá»u trong quáșŁn lĂœ nhĂąn sá»±
XĂąy dá»±ng cÆĄ sá» dữ liá»u trong quáșŁn lĂœ nhĂąn sá»±AskSock NgĂŽ Quang ÄáșĄo
Ìę
TĂ i liá»u trĂŹnh bĂ y cĂĄch xĂąy dá»±ng cÆĄ sá» dữ liá»u trong quáșŁn lĂœ nhĂąn sá»±, bao gá»m tá»ng quan vá» há» thá»ng quáșŁn lĂœ, cĂĄc chức nÄng, nhiá»m vỄ vĂ yĂȘu cáș§u của há» thá»ng. NĂł cĆ©ng Äá» cáșp Äáșżn viá»c thiáșżt káșż mĂŽ hĂŹnh cÆĄ sá» dữ liá»u, phĂąn tĂch cĂĄc báșŁng dữ liá»u cáș§n thiáșżt vĂ thá»±c hiá»n chuáș©n hĂła. Cuá»i cĂčng, tĂ i liá»u giá»i thiá»u cĂĄch sá» dỄng Microsoft Access vĂ SQL Äá» quáșŁn lĂœ vĂ truy xuáș„t dữ liá»u hiá»u quáșŁ.BĂ i táșp sá» phức
BĂ i táșp sá» phứcphuonganhtran1303
Ìę
Sá» phức cĂł dáșĄng a + bi, trong ÄĂł a vĂ b lĂ sá» thá»±c, vĂ i lĂ ÄÆĄn vá» áșŁo vá»i iÂČ = -1. CĂĄc phĂ©p toĂĄn nhÆ° cá»ng, trừ, nhĂąn vĂ chia sá» phức, cĆ©ng nhÆ° biá»u diá»
n hĂŹnh há»c trĂȘn máș·t pháșłng tá»a Äá», Äá»u ÄÆ°á»Łc Äá»nh nghÄ©a rĂ” rĂ ng trong tĂ i liá»u. NgoĂ i ra, tĂ i liá»u cĂČn Äá» cáșp Äáșżn dáșĄng lÆ°á»Łng giĂĄc của sá» phức vĂ cĂĄc phÆ°ÆĄng phĂĄp giáșŁi toĂĄn cÆĄ báșŁn liĂȘn quan Äáșżn sá» phức.Luáșn vÄn: Biáșżn Äá»i Laplace vĂ má»t sỠứng dỄng, HAY, 9Ä
Luáșn vÄn: Biáșżn Äá»i Laplace vĂ má»t sỠứng dỄng, HAY, 9ÄDá»ch vỄ viáșżt bĂ i trá»n gĂłi ZALO: 0909232620
Ìę
Luáșn vÄn tháșĄc sÄ© nĂ y nghiĂȘn cứu vá» biáșżn Äá»i Laplace, má»t phĂ©p biáșżn Äá»i tĂch phĂąn quan trá»ng, vĂ cĂĄc ứng dỄng của nĂł trong giáșŁi quyáșżt cĂĄc phÆ°ÆĄng trĂŹnh vi phĂąn vĂ bĂ i toĂĄn liĂȘn quan. TĂ i liá»u trĂŹnh bĂ y lĂœ thuyáșżt cÆĄ báșŁn, tĂnh cháș„t vĂ cĂĄc phÆ°ÆĄng phĂĄp tĂŹm biáșżn Äá»i Laplace ngÆ°á»Łc, cĂčng vá»i cĂĄc ứng dỄng trong váșt lĂœ vĂ khoa há»c ká»č thuáșt. NghiĂȘn cứu cĆ©ng bao gá»m cĂĄc Äiá»u kiá»n tá»n táșĄi vĂ cĂĄc vĂ dỄ cỄ thá» vá» biáșżn Äá»i Laplace.BĂ i giáșŁng xĂĄc suáș„t thá»ng kĂȘ
BĂ i giáșŁng xĂĄc suáș„t thá»ng kĂȘHá»c Huỳnh BĂĄ
Ìę
TĂ i liá»u cung cáș„p kiáșżn thức cÆĄ báșŁn vá» xĂĄc suáș„t vĂ thá»ng kĂȘ, báșŻt Äáș§u từ cĂĄc khĂĄi niá»m vá» hiá»n tÆ°á»Łng ngáș«u nhiĂȘn, biáșżn cá», vĂ cĂĄc phĂ©p toĂĄn liĂȘn quan Äáșżn biáșżn cá». NĂł giáșŁi thĂch cĂĄch xĂĄc Äá»nh xĂĄc suáș„t của cĂĄc biáșżn cá» thĂŽng qua cĂĄc phÆ°ÆĄng phĂĄp cá» Äiá»n vĂ thá»ng kĂȘ, cĆ©ng nhÆ° cĂĄc khĂĄi niá»m liĂȘn quan Äáșżn báșŁng phĂąn phá»i táș§n sá». NgoĂ i ra, tĂ i liá»u cĆ©ng Äá» cáșp Äáșżn quy trĂŹnh thu tháșp vĂ phĂąn tĂch dữ liá»u trong nghiĂȘn cứu thá»ng kĂȘ.Ma tráșn - Äá»nh thức vĂ cĂĄc ứng dỄng trong kinh táșż
Ma tráșn - Äá»nh thức vĂ cĂĄc ứng dỄng trong kinh táșżngTonH1
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» ma tráșn vĂ cĂĄc phĂ©p toĂĄn tuyáșżn tĂnh trong bá» mĂŽn toĂĄn kinh táșż vĂ khoa há»c dữ liá»u, bao gá»m cĂĄc khĂĄi niá»m cÆĄ báșŁn vá» ma tráșn, cĂĄc dáșĄng ma tráșn nhÆ° ma tráșn vuĂŽng, tam giĂĄc, ÄÆ°á»ng chĂ©o vĂ ÄÆĄn vá». NgoĂ i ra, tĂ i liá»u cĂČn nĂȘu rĂ” cĂĄc phĂ©p toĂĄn tuyáșżn tĂnh, vĂ dỄ thá»±c táșż vĂ tĂnh cháș„t của phĂ©p toĂĄn Äá»i vá»i cĂĄc ma tráșn. Cuá»i cĂčng, tĂ i liá»u cung cáș„p cĂĄc phÆ°ÆĄng phĂĄp tĂnh Äá»nh thức vĂ nhĂąn ma tráșn.PhÆ°ÆĄng phĂĄp runge kutta giáșŁi gáș§n ÄĂșng há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá»
PhÆ°ÆĄng phĂĄp runge kutta giáșŁi gáș§n ÄĂșng há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá»Khu Tiáșżn
Ìę
Luáșn vÄn của VĆ© Huy BĂŹnh trĂŹnh bĂ y vá» phÆ°ÆĄng phĂĄp Runge-Kutta Äá» giáșŁi gáș§n ÄĂșng há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá», má»t lÄ©nh vá»±c cĂł nhiá»u ứng dỄng thá»±c tiá»
n trong cĂĄc ngĂ nh khoa há»c vĂ ká»č thuáșt. TĂĄc giáșŁ ÄĂŁ chia luáșn vÄn thĂ nh ba chÆ°ÆĄng, gá»m cĂĄc khĂĄi niá»m cÆĄ báșŁn vá» há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá», phÆ°ÆĄng phĂĄp Runge-Kutta, và ứng dỄng của phÆ°ÆĄng phĂĄp nĂ y qua cĂĄc vĂ dỄ cỄ thá». Luáșn vÄn ÄÆ°á»Łc hoĂ n thĂ nh dÆ°á»i sá»± hÆ°á»ng dáș«n của TS. Nguyá»
n VÄn Minh táșĄi ÄáșĄi há»c ThĂĄi NguyĂȘn vĂ o nÄm 2012.Äáș I Sá» TUYáșŸN TĂNH.pdf
Äáș I Sá» TUYáșŸN TĂNH.pdf0058NguynVHongSn
Ìę
TĂ i liá»u chủ yáșżu Äá» cáșp Äáșżn cĂĄc khĂĄi niá»m vĂ phĂ©p toĂĄn liĂȘn quan Äáșżn ma tráșn, bao gá»m Äá»nh thức, há» phÆ°ÆĄng trĂŹnh, khĂŽng gian vector vĂ ĂĄnh xáșĄ tuyáșżn tĂnh. NĂł bao gá»m cĂĄc ná»i dung nhÆ° phĂ©p cá»ng, trừ, nhĂąn ma tráșn vĂ lĆ©y thừa của ma tráșn, cĆ©ng nhÆ° cĂĄc biáșżn Äá»i sÆĄ cáș„p trĂȘn ma tráșn. TĂ i liá»u cĂČn giáșŁi thĂch chi tiáșżt vá» cĂĄc loáșĄi ma tráșn nhÆ° ma tráșn khĂŽng, ma tráșn kháșŁ nghá»ch, vĂ cĂĄc tĂnh cháș„t của chĂșng.Luáșn vÄn: GiáșŁi bĂ i toĂĄn Dirichlet Äá»i vá»i phÆ°ÆĄng trĂŹnh Elliptic, 9Ä
Luáșn vÄn: GiáșŁi bĂ i toĂĄn Dirichlet Äá»i vá»i phÆ°ÆĄng trĂŹnh Elliptic, 9ÄDá»ch vỄ viáșżt bĂ i trá»n gĂłi ZALO 0917193864
Ìę
Luáșn vÄn tháșĄc sá»č của BĂči Thá» Oanh nghiĂȘn cứu vá» phÆ°ÆĄng phĂĄp nghiá»m trĂȘn nghiá»m dÆ°á»i Äá» giáșŁi bĂ i toĂĄn Dirichlet cho phÆ°ÆĄng trĂŹnh elliptic. TĂ i liá»u bao gá»m ba chÆ°ÆĄng, trong ÄĂł trĂŹnh bĂ y cĂĄc kiáșżn thức cÆĄ báșŁn vá» khĂŽng gian Sobolev, toĂĄn tá» vi phĂąn elliptic và ứng dỄng của phÆ°ÆĄng phĂĄp láș·p ÄÆĄn Äiá»u. BĂȘn cáșĄnh ÄĂł, luáșn vÄn cĆ©ng cung cáș„p chứng minh vĂ vĂ dỄ ĂĄp dỄng nháș±m phĂĄt triá»n lĂœ thuyáșżt vĂ phÆ°ÆĄng phĂĄp liĂȘn quan Äáșżn bĂ i toĂĄn Dirichlet ná»a tuyáșżn tĂnh.Bai7 khai trien_taylor
Bai7 khai trien_taylorljmonking
Ìę
TĂ i liá»u trĂŹnh bĂ y cĂŽng thức khai triá»n Taylor vĂ cĂĄc pháș§n dÆ° Lagrange cĆ©ng nhÆ° Peano, cĂčng vá»i vĂ dỄ minh há»a cỄ thá» cho viá»c khai triá»n cĂĄc hĂ m sá» nhÆ° sin, tan vĂ cĂĄc Äa thức. TĂ i liá»u giáșŁi thĂch Ăœ nghÄ©a của khai triá»n Taylor trong viá»c ÄÆĄn giáșŁn hĂła tĂnh toĂĄn vá»i cĂĄc hĂ m phức táșĄp thĂŽng qua cĂĄc Äa thức. NĂł cĆ©ng Äá» cáșp Äáșżn cĂĄc phÆ°ÆĄng phĂĄp khai triá»n Äáșżn cáș„p Äá» khĂĄc nhau vĂ cĂĄch ĂĄp dỄng chĂșng trong cĂĄc trÆ°á»ng hợp cỄ thá».Luáșn vÄn: Biáșżn Äá»i Laplace vĂ má»t sỠứng dỄng, HAY, 9Ä
Luáșn vÄn: Biáșżn Äá»i Laplace vĂ má»t sỠứng dỄng, HAY, 9ÄDá»ch vỄ viáșżt bĂ i trá»n gĂłi ZALO: 0909232620
Ìę
PhÆ°ÆĄng phĂĄp runge kutta giáșŁi gáș§n ÄĂșng há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá»
PhÆ°ÆĄng phĂĄp runge kutta giáșŁi gáș§n ÄĂșng há» phÆ°ÆĄng trĂŹnh vi phĂąn ÄáșĄi sá»Khu Tiáșżn
Ìę
Luáșn vÄn: GiáșŁi bĂ i toĂĄn Dirichlet Äá»i vá»i phÆ°ÆĄng trĂŹnh Elliptic, 9Ä
Luáșn vÄn: GiáșŁi bĂ i toĂĄn Dirichlet Äá»i vá»i phÆ°ÆĄng trĂŹnh Elliptic, 9ÄDá»ch vỄ viáșżt bĂ i trá»n gĂłi ZALO 0917193864
Ìę
Similar to 04 hang ma tran (20)
04 hangmatran
04 hangmatranLĂȘ CĂŽng Tuáș„n Anh
Ìę
TĂ i liá»u trĂŹnh bĂ y khĂĄi niá»m 'háșĄng ma tráșn' trong ÄáșĄi sá» tuyáșżn tĂnh, giĂșp xĂĄc Äá»nh cĂĄc trÆ°á»ng hợp của há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh, bao gá»m há» vĂŽ nghiá»m, cĂł nghiá»m duy nháș„t hoáș·c cĂł vĂŽ sá» nghiá»m. HáșĄng ma tráșn ÄÆ°á»Łc so sĂĄnh giữa ma tráșn há» sá» vĂ ma tráșn há» sá» má» rá»ng Äá» xĂĄc Äá»nh loáșĄi nghiá»m của há» phÆ°ÆĄng trĂŹnh. TĂ i liá»u cung cáș„p cĂĄc vĂ dỄ vĂ bĂ i táșp vá» viá»c xĂĄc Äá»nh háșĄng ma tráșn.01 matran
01 matranLĂȘ CĂŽng Tuáș„n Anh
Ìę
TĂ i liá»u cung cáș„p kiáșżn thức cÆĄ báșŁn vá» ma tráșn vĂ cĂĄc loáșĄi ma tráșn trong ÄáșĄi sá» tuyáșżn tĂnh, bao gá»m ma tráșn khĂŽng, ma tráșn vuĂŽng, ma tráșn chĂ©o, vĂ cĂĄc ma tráșn Äáș·c biá»t khĂĄc. NgoĂ i ra, tĂ i liá»u cĂČn trĂŹnh bĂ y cĂĄc phĂ©p toĂĄn trĂȘn ma tráșn nhÆ° phĂ©p cá»ng vĂ phĂ©p nhĂąn vá»i má»t sá». CĂĄc vĂ dỄ cỄ thá» ÄÆ°á»Łc ÄÆ°a ra Äá» minh há»a cho từng loáșĄi ma tráșn vĂ phĂ©p toĂĄn.12.ma tráșn vĂ dá»nh thức
12.ma tráșn vĂ dá»nh thứcTrinh Yen
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» ma tráșn, bao gá»m Äá»nh nghÄ©a, cĂĄc loáșĄi ma tráșn nhÆ° ma tráșn vuĂŽng, ma tráșn tam giĂĄc, vĂ ma tráșn ÄÆĄn vá». NĂł cĆ©ng Äá» cáșp Äáșżn cĂĄc phĂ©p toĂĄn trĂȘn ma tráșn, cĂĄch tĂnh Äá»nh thức, ma tráșn nghá»ch ÄáșŁo, vĂ phÆ°ÆĄng phĂĄp tĂŹm háșĄng ma tráșn. Cuá»i cĂčng, tĂ i liá»u bao gá»m cĂĄc bĂ i táșp minh há»a và ứng dỄng của ma tráșn trong viá»c giáșŁi phÆ°ÆĄng trĂŹnh.BaitapDSTT.pdf
BaitapDSTT.pdfHHng264614
Ìę
TĂ i liá»u bao gá»m nhiá»u bĂ i toĂĄn liĂȘn quan Äáșżn ma tráșn vĂ Äá»nh thức, từ viá»c tĂnh toĂĄn cĂĄc phĂ©p toĂĄn trĂȘn ma tráșn Äáșżn viá»c tĂŹm háșĄng vĂ ma tráșn nghá»ch ÄáșŁo. NĂł cĆ©ng Äá» cáșp Äáșżn viá»c giáșŁi cĂĄc há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh vĂ nghiĂȘn cứu cĂĄc tĂnh cháș„t của cĂĄc ma tráșn trong cĂĄc bĂ i toĂĄn cỄ thá». Ná»i dung ÄÆ°á»Łc tá» chức theo cĂĄc bĂ i táșp vá»i nhiá»u dáșĄng toĂĄn khĂĄc nhau liĂȘn quan Äáșżn ma tráșn.Tcca2.TranThiTuyetLan
Tcca2.TranThiTuyetLanLong Tran Huy
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» ma tráșn vĂ há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh, bao gá»m cĂĄc khĂĄi niá»m cÆĄ báșŁn vá» ma tráșn, phĂ©p biáșżn Äá»i sÆĄ cáș„p, vĂ cĂĄc loáșĄi ma tráșn Äáș·c biá»t nhÆ° ma tráșn ÄÆĄn vá», ma tráșn tam giĂĄc, vĂ ma tráșn chuyá»n vá». NĂł cĆ©ng Äá» cáșp Äáșżn cĂĄc phĂ©p toĂĄn trĂȘn ma tráșn nhÆ° cá»ng, trừ vĂ nhĂąn ma tráșn, cĂčng vá»i vĂ dỄ minh há»a cho từng khĂĄi niá»m. NgoĂ i ra, tĂ i liá»u nĂȘu rĂ” cĂĄc tĂnh cháș„t của cĂĄc phĂ©p toĂĄn vĂ sá»± tá»n táșĄi của tĂch ma tráșn.ChÆ°ÆĄng 2_CĂĄc pp sá» trong ÄáșĄi sá» tuyáșżn tĂnh.pdf
ChÆ°ÆĄng 2_CĂĄc pp sá» trong ÄáșĄi sá» tuyáșżn tĂnh.pdfhOALE997210
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» cĂĄc phÆ°ÆĄng phĂĄp sá» trong ÄáșĄi sá» tuyáșżn tĂnh, bao gá»m ma tráșn, Äá»nh thức, giĂĄ trá» riĂȘng vĂ vector riĂȘng. NĂł cung cáș„p cĂĄc Äáș·c Äiá»m của ma tráșn, phÆ°ÆĄng phĂĄp tĂnh Äá»nh thức vĂ ma tráșn nghá»ch ÄáșŁo, cĆ©ng nhÆ° há» phÆ°ÆĄng trĂŹnh ÄáșĄi sá» tuyáșżn tĂnh vĂ cĂĄc phÆ°ÆĄng phĂĄp giáșŁi, nhÆ° khá» Gauss-Jordan. TĂ i liá»u nĂ y cĂł mỄc tiĂȘu hÆ°á»ng dáș«n vĂ há» trợ sinh viĂȘn trong viá»c hiá»u vĂ ĂĄp dỄng cĂĄc khĂĄi niá»m toĂĄn há»c liĂȘn quan.Tuáș§n 1_matráșn_PhĂ©p toĂĄn_BÄsc.pptx
Tuáș§n 1_matráșn_PhĂ©p toĂĄn_BÄsc.pptxPHONGDNGQUC2
Ìę
TĂ i liá»u Äá» cáșp Äáșżn chÆ°ÆĄng 2 của mĂŽn ÄáșĄi sá» tuyáșżn tĂnh, táșp trung vĂ o ma tráșn, Äá»nh thức vĂ há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh. NĂł bao gá»m cĂĄc Äá»nh nghÄ©a cÆĄ báșŁn vá» ma tráșn, cĂĄc loáșĄi ma tráșn, phĂ©p toĂĄn trĂȘn ma tráșn vĂ cĂĄc phĂ©p biáșżn Äá»i sÆĄ cáș„p. HÆĄn nữa, tĂ i liá»u cĆ©ng trĂŹnh bĂ y vá» háșĄng của ma tráșn vĂ cĂĄc vĂ dỄ minh há»a liĂȘn quan.Ch1.DSTT_șĘșĘߣs.pdf
Ch1.DSTT_șĘșĘߣs.pdfTrá»nh NhÆ° Quỳnh
Ìę
TĂ i liá»u bĂ i giáșŁng vá» ÄáșĄi sá» tuyáșżn tĂnh gá»m nhiá»u pháș§n táșp trung vĂ o ma tráșn, Äá»nh thức vĂ há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh. ChÆ°ÆĄng Äáș§u tiĂȘn giáșŁi thĂch khĂĄi niá»m ma tráșn, cĂĄc phĂ©p toĂĄn trĂȘn ma tráșn, vĂ cĂĄc tĂnh cháș„t của Äá»nh thức. NĂł cĆ©ng Äá»nh nghÄ©a háșĄng của ma tráșn vĂ những phĂ©p biáșżn Äá»i sÆĄ cáș„p trĂȘn ma tráșn.Tuáș§n 1_matráșn_PhĂ©p toĂĄn_BÄsc,Äáș·ng VÄn Vinh.ppt
Tuáș§n 1_matráșn_PhĂ©p toĂĄn_BÄsc,Äáș·ng VÄn Vinh.pptkhavophik2024
Ìę
TĂ i liá»u nĂ y lĂ giĂĄo trĂŹnh ÄáșĄi sá» tuyáșżn tĂnh, trĂŹnh bĂ y khĂĄi niá»m cÆĄ báșŁn vá» ma tráșn, Äá»nh thức, há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh vĂ cĂĄc khĂĄi niá»m liĂȘn quan. NĂł bao gá»m Äá»nh nghÄ©a vá» cĂĄc loáșĄi ma tráșn, phĂ©p toĂĄn giữa cĂĄc ma tráșn, vĂ cĂĄc phÆ°ÆĄng phĂĄp biáșżn Äá»i sÆĄ cáș„p Äá» giáșŁi há» phÆ°ÆĄng trĂŹnh. Ná»i dung cĆ©ng cung cáș„p cĂĄch ÄĂĄnh giĂĄ dĂ nh cho mĂŽn há»c, bao gá»m thi giữa kỳ, bĂ i táșp lá»n vĂ thi cuá»i kỳ.Bai tap-dai-so-tuyen-tinh-co-giai
Bai tap-dai-so-tuyen-tinh-co-giaigiaoduc0123
Ìę
TĂ i liá»u lĂ bĂ i táșp ĂŽn táșp ÄáșĄi sá» tuyáșżn tĂnh há»c kỳ I nÄm há»c 2016-2017, bao gá»m nhiá»u bĂ i táșp khĂĄc nhau nhÆ° tĂnh toĂĄn ma tráșn, Äá»nh thức, háșĄng, phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh vĂ khĂŽng gian vĂ©c tÆĄ. Má»i bĂ i táșp ÄÆ°a ra cĂĄc ma tráșn cỄ thá» vá»i yĂȘu cáș§u thá»±c hiá»n cĂĄc phĂ©p toĂĄn hoáș·c tĂŹm kiáșżm cĂĄc tĂnh cháș„t toĂĄn há»c. CĂĄc bĂ i táșp yĂȘu cáș§u ngÆ°á»i há»c giáșŁi quyáșżt vĂ cho biáșżt cĂĄc káșżt quáșŁ cỄ thá» liĂȘn quan Äáșżn ma tráșn.phuong-phap-so_le-thanh-long_chuong-2_cac-pp-so-trong-dai-so-tuyen-tinh - [cu...
phuong-phap-so_le-thanh-long_chuong-2_cac-pp-so-trong-dai-so-tuyen-tinh - [cu...quanganhfo4
Ìę
phÆ°ÆĄng phĂĄp sá»
03 matrannghichdao
03 matrannghichdaoLĂȘ CĂŽng Tuáș„n Anh
Ìę
TĂ i liá»u giá»i thiá»u vá» ma tráșn nghá»ch ÄáșŁo trong ÄáșĄi sá» tuyáșżn tĂnh, bao gá»m cĂĄch xĂĄc Äá»nh ma tráșn vĂ giáșŁi há» phÆ°ÆĄng trĂŹnh dÆ°á»i dáșĄng ma tráșn. Má»t sá» vĂ dỄ vá» viá»c tĂŹm ma tráșn nghá»ch ÄáșŁo cĆ©ng nhÆ° xá» lĂœ há» phÆ°ÆĄng trĂŹnh ÄÆ°á»Łc trĂŹnh bĂ y. NgoĂ i ra, má»t sá» bĂ i táșp liĂȘn quan Äáșżn viá»c tĂŹm ma tráșn phỄ hợp vĂ ma tráșn nghá»ch ÄáșŁo cĆ©ng ÄÆ°á»Łc ÄÆ°a ra.DSTT Lecture 1.pptx
DSTT Lecture 1.pptxDiNgu2
Ìę
TĂ i liá»u trĂŹnh bĂ y ná»i dung vá» ÄáșĄi sá» tuyáșżn tĂnh, bao gá»m cĂĄc khĂĄi niá»m cÆĄ báșŁn nhÆ° ma tráșn, há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh, Äá»nh thức, khĂŽng gian vector vĂ cĂĄc phĂ©p toĂĄn trĂȘn ma tráșn. NĂł cĆ©ng Äá» cáșp Äáșżn cĂĄc ứng dỄng thá»±c tiá»
n nhÆ° mĂĄy há»c, mĂŁ hĂła, vĂ cĂĄc mĂŽ hĂŹnh kinh táșż. ThĂŽng tin vá» cĂĄch tĂnh Äiá»m vĂ cáș„u trĂșc khĂła há»c cĆ©ng ÄÆ°á»Łc nĂȘu rĂ”, cĂčng vá»i cĂĄc tĂ i liá»u tham kháșŁo.TĂŹm trá» riĂȘng báș±ng pp qr
TĂŹm trá» riĂȘng báș±ng pp qrToĂ n Phan
Ìę
TĂ i liá»u trĂŹnh bĂ y phÆ°ÆĄng phĂĄp tĂŹm trá» riĂȘng của ma tráșn báș±ng cĂĄch sá» dỄng phĂąn tĂch QR vĂ biáșżn Äá»i ma tráșn Äá»i xứng. CĂĄc bÆ°á»c thá»±c hiá»n bao gá»m viá»c sá» dỄng ma tráșn quay P vĂ ĂĄp dỄng thuáșt toĂĄn QR tá»nh tiáșżn Äá» tĂŹm cĂĄc trá» riĂȘng của ma tráșn. VĂ dỄ minh há»a lĂ má»t ma tráșn vuĂŽng 3x3 vá»i cĂĄc bÆ°á»c cỄ thá» vĂ cĂŽng thức cáș§n thiáșżt Äá» hoĂ n thĂ nh quĂĄ trĂŹnh.biáșżn Äá»i ma tráșn ( Transformation matrix)
biáșżn Äá»i ma tráșn ( Transformation matrix)Bui Loi
Ìę
TĂ i liá»u trĂŹnh bĂ y cĂĄc dáșĄng bĂ i toĂĄn ĂŽn táșp mĂŽn toĂĄn, bao gá»m tĂnh Äá»nh thức, giáșŁi há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh, xĂĄc Äá»nh háșĄng của ma tráșn, tĂŹm ma tráșn nghá»ch ÄáșŁo, vĂ xĂĄc Äá»nh phỄ thuá»c/Äá»c láșp tuyáșżn tĂnh. CĂĄc bĂ i toĂĄn ÄÆ°á»Łc minh há»a kĂšm theo quy trĂŹnh giáșŁi chi tiáșżt vĂ phÆ°ÆĄng phĂĄp sá» dỄng ma tráșn. Ná»i dung chủ yáșżu hÆ°á»ng dáș«n cĂĄch ĂĄp dỄng lĂœ thuyáșżt ÄáșĄi sá» tuyáșżn tĂnh vĂ o giáșŁi quyáșżt cĂĄc bĂ i toĂĄn cỄ thá».ChÆ°ÆĄng 1.pdf
ChÆ°ÆĄng 1.pdfKitTun101816
Ìę
TĂ i liá»u trĂŹnh bĂ y ná»i dung vá» ÄáșĄi sá» tuyáșżn tĂnh vá»i tá»ng cá»ng 30 tiáșżt, bao gá»m cĂĄc chủ Äá» từ ma tráșn, Äá»nh thức, há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh, khĂŽng gian vectÆĄ Äáșżn ĂĄnh xáșĄ tuyáșżn tĂnh. ÄĂĄnh giĂĄ há»c pháș§n bao gá»m 30% cho quĂĄ trĂŹnh há»c táșp vĂ 70% cho kỳ thi tráșŻc nghiá»m. TĂ i liá»u tham kháșŁo chĂnh vĂ cĂĄc vĂ dỄ minh há»a cĆ©ng ÄÆ°á»Łc cung cáș„p Äá» há» trợ sinh viĂȘn trong quĂĄ trĂŹnh há»c táșp.Tiá»u luáșn ToĂĄn cao cáș„p.docx
Tiá»u luáșn ToĂĄn cao cáș„p.docxXunYn4
Ìę
TĂ i liá»u lĂ bĂĄo cĂĄo há»c pháș§n toĂĄn cao cáș„p 1 của sinh viĂȘn PhĂč XuĂąn Yáșżn táșĄi trÆ°á»ng ÄáșĄi há»c Lao Äá»ng â XĂŁ há»i. NĂł bao gá»m ÄĂĄnh giĂĄ của giáșŁng viĂȘn vĂ trĂŹnh bĂ y cĂĄc bĂ i táșp giáșŁi ma tráșn, tĂnh Äá»nh thức vĂ há» phÆ°ÆĄng trĂŹnh. Ná»i dung chủ yáșżu xoay quanh cĂĄc phĂ©p toĂĄn ÄáșĄi sá» tuyáșżn tĂnh vĂ phÆ°ÆĄng trĂŹnh ma tráșn.Phuong trinh mu t sy
Phuong trinh mu t syHuynh ICT
Ìę
TĂ i liá»u lĂ hÆ°á»ng dáș«n giáșŁi cĂĄc bĂ i táșp vá» phÆ°ÆĄng trĂŹnh mĆ©, bao gá»m nhiá»u phÆ°ÆĄng trĂŹnh khĂĄc nhau cĂčng vá»i cĂĄc bÆ°á»c giáșŁi chi tiáșżt. NĂł ÄÆ°á»Łc soáșĄn tháșŁo bá»i Nguyá»
n ÄĂŹnh Sá»č vĂ o thĂĄng 7 nÄm 2011 vĂ chứa nhiá»u vĂ dỄ minh há»a. Má»i bĂ i táșp Äá»u Äi kĂšm vá»i phĂąn tĂch vĂ giáșŁi thĂch rĂ” rĂ ng.Phuong trinh mu t sy
Phuong trinh mu t syHuynh ICT
Ìę
TĂ i liá»u giáșŁi bĂ i táșp vá» phÆ°ÆĄng trĂŹnh mĆ© do Nguyá»
n ÄĂŹnh Sá»č biĂȘn soáșĄn, cung cáș„p hÆ°á»ng dáș«n giáșŁi cho nhiá»u phÆ°ÆĄng trĂŹnh mĆ© khĂĄc nhau. Má»i bĂ i táșp Äá»u cĂł biáșżn Äá»i vĂ lĂœ luáșn chi tiáșżt rĂ” rĂ ng Äá» tĂŹm ra nghiá»m của phÆ°ÆĄng trĂŹnh. TĂ i liá»u nĂ y cĂł thá» hữu Ăch cho viá»c ĂŽn luyá»n vĂ cáșŁi thiá»n ká»č nÄng giáșŁi toĂĄn liĂȘn quan Äáșżn phÆ°ÆĄng trĂŹnh mĆ©.Chuong03
Chuong03caovanquy
Ìę
ChÆ°ÆĄng trĂŹnh nháș±m giá»i thiá»u phÆ°ÆĄng phĂĄp sá» trong ÄáșĄi sá» tuyáșżn tĂnh vá»i cĂĄc cĂĄch giáșŁi há» phÆ°ÆĄng trĂŹnh tuyáșżn tĂnh, bao gá»m phÆ°ÆĄng phĂĄp Cramer vĂ phÆ°ÆĄng phĂĄp Gauss. PhÆ°ÆĄng phĂĄp Cramer lĂ phÆ°ÆĄng phĂĄp chĂnh xĂĄc ÄĂČi há»i tĂnh toĂĄn nhiá»u Äá»nh thức, trong khi phÆ°ÆĄng phĂĄp Gauss thá»±c hiá»n quĂĄ trĂŹnh biáșżn Äá»i ma tráșn vĂ giáșŁi ngÆ°á»Łc Äá» tĂŹm nghiá»m há». Cuá»i cĂčng, phÆ°ÆĄng phĂĄp Cholesky ÄÆ°á»Łc trĂŹnh bĂ y nhÆ° má»t cĂĄch giáșŁi há» qua viá»c phĂąn tĂch ma tráșn thĂ nh tĂch của hai ma tráșn tam giĂĄc.Ad
More from NguyỠn PhỄng (12)
Bt chuong 4,5,6
Bt chuong 4,5,6Nguyá»
n PhỄng
Ìę
BĂ i táșp nĂ y liĂȘn quan Äáșżn cĂĄc khĂĄi niá»m trong khĂŽng gian R^3 vĂ ma tráșn, bao gá»m viá»c kiá»m tra tĂch vĂŽ hÆ°á»ng, trá»±c giao hĂła cĂĄc há» vector, chuáș©n hĂła, tĂŹm giĂĄ trá» riĂȘng vĂ vector riĂȘng của ma tráșn, cĆ©ng nhÆ° chuyá»n Äá»i cĂĄc dáșĄng toĂ n phÆ°ÆĄng vá» dáșĄng chĂnh táșŻc qua cĂĄc phÆ°ÆĄng phĂĄp Lagrange vĂ chĂ©o hĂła trá»±c giao.Bt chÆ°ÆĄng 1
Bt chÆ°ÆĄng 1Nguyá»
n PhỄng
Ìę
TĂ i liá»u chứa cĂĄc bĂ i táșp vá» ÄáșĄi sá», bao gá»m tĂnh toĂĄn ma tráșn, Äá»nh thức vĂ nghiĂȘn cứu cĂĄc tĂnh cháș„t của chĂșng. CĂĄc bĂ i táșp yĂȘu cáș§u xĂĄc Äá»nh má»t sá» giĂĄ trá» cỄ thá», tĂŹm ma tráșn giao hoĂĄn, vĂ chứng minh má»t sá» cĂŽng thức ÄáșĄi sá». NgoĂ i ra, tĂ i liá»u cĆ©ng Äá» cáșp Äáșżn cĂĄch giáșŁi cĂĄc phÆ°ÆĄng trĂŹnh há» ma tráșn vĂ Äiá»u kiá»n tá»n táșĄi ma tráșn nghá»ch ÄáșŁo.Bt chuong 3
Bt chuong 3Nguyá»
n PhỄng
Ìę
TĂ i liá»u yĂȘu cáș§u kiá»m tra xem cĂĄc táșp hợp vector vá»i phĂ©p toĂĄn cá»ng vĂ nhĂąn vĂŽ hÆ°á»ng cĂł pháșŁi lĂ khĂŽng gian vector hay khĂŽng, Äá»ng thá»i tĂnh ÄáșĄi sá» cho má»t sá» vector vĂ Äiá»u kiá»n cho tĂnh Äá»c láșp tuyáșżn tĂnh. CĂĄc bĂ i toĂĄn liĂȘn quan Äáșżn khĂŽng gian con, cÆĄ sá», chiá»u khĂŽng gian, vĂ nghiá»m của há» phÆ°ÆĄng trĂŹnh cĆ©ng ÄÆ°á»Łc Äá» cáșp. NgoĂ i ra, tĂ i liá»u cĂČn yĂȘu cáș§u tĂŹm ma tráșn chuyá»n cÆĄ sá» vĂ Äiá»u kiá»n Äá» cĂĄc há» vector lĂ cÆĄ sá» của khĂŽng gian R^3.Bt chÆ°ÆĄng 2
Bt chÆ°ÆĄng 2Nguyá»
n PhỄng
Ìę
TĂ i liá»u gá»m cĂĄc bĂ i táșp vá» viá»c giáșŁi vĂ biá»n luáșn há» phÆ°ÆĄng trĂŹnh vá»i nhiá»u biáșżn sá». CĂĄc bĂ i táșp yĂȘu cáș§u xá» lĂœ cĂĄc há» phÆ°ÆĄng trĂŹnh phức táșĄp, xĂĄc Äá»nh Äiá»u kiá»n vĂ giĂĄ trá» tham sá» m, a, b, c Äá» há» cĂł nghiá»m. Ná»i dung nĂ y cĂł thá» dĂčng cho viá»c ĂŽn luyá»n cho cĂĄc kỳ thi hoáș·c bĂ i kiá»m tra trong mĂŽn toĂĄn.Bt chÆ°ÆĄng 1
Bt chÆ°ÆĄng 1Nguyá»
n PhỄng
Ìę
TĂ i liá»u chứa cĂĄc bĂ i táșp liĂȘn quan Äáșżn ma tráșn vĂ Äá»nh thức, bao gá»m viá»c tĂnh toĂĄn giĂĄ trá» của cĂĄc ma tráșn, Äá»nh thức vĂ Äiá»u kiá»n Äá» má»t ma tráșn cĂł nghiá»m. NĂł cĆ©ng yĂȘu cáș§u tĂŹm cĂĄc ma tráșn giao hoĂĄn vĂ kiá»m tra tĂnh háșĄng của má»t sá» ma tráșn vá»i cĂĄc tham sá» khĂĄc nhau.Thdc 05
Thdc 05Nguyá»
n PhỄng
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» cĂĄc nguyĂȘn lĂœ cÆĄ báșŁn của tin há»c, bao gá»m cĂĄch mĂĄy tĂnh hoáșĄt Äá»ng vĂ cĂĄch thĂŽng tin ÄÆ°á»Łc biá»u diá»
n vĂ xá» lĂœ báș±ng sá» nhá» phĂąn. NĂł giáșŁi thĂch cĂĄc ÄÆĄn vá» dữ liá»u nhÆ° bit, byte cĆ©ng nhÆ° cĂĄc phÆ°ÆĄng phĂĄp biá»u diá»
n sá» Ăąm nhÆ° dáș„u lÆ°á»Łng vĂ bĂč 2. HÆĄn nữa, tĂ i liá»u Äá» cáșp Äáșżn cĂĄc phĂ©p toĂĄn sá» há»c trong há» nhá» phĂąn vĂ cĂĄc váș„n Äá» liĂȘn quan Äáșżn trĂ n sá».Giaotrinhc++
Giaotrinhc++Nguyá»
n PhỄng
Ìę
GiĂĄo trĂŹnh láșp trĂŹnh C cÆĄ báșŁn cung cáș„p cĂĄc kiáșżn thức vá» ngĂŽn ngữ láșp trĂŹnh, cĂĄc bÆ°á»c láșp trĂŹnh vĂ ká»č thuáșt láșp trĂŹnh. TĂ i liá»u bao gá»m nhiá»u bĂ i há»c từ cĂĄc khĂĄi niá»m cÆĄ báșŁn vá» láșp trĂŹnh Äáșżn cĂĄc cáș„u trĂșc Äiá»u khiá»n, vĂČng láș·p, hĂ m, máșŁng, con trá» vĂ má»t sá» hĂ m chuáș©n. MỄc tiĂȘu lĂ giĂșp há»c viĂȘn náșŻm báșŻt cĂĄc kiáșżn thức cáș§n thiáșżt Äá» láșp trĂŹnh vĂ phĂĄt triá»n ứng dỄng trong ngĂŽn ngữ C.Giao trinh c_can_ban
Giao trinh c_can_banNguyá»
n PhỄng
Ìę
TĂ i liá»u lĂ giĂĄo trĂŹnh láșp trĂŹnh C cÄn báșŁn, bao gá»m nhiá»u chủ Äá» nhÆ° ngĂŽn ngữ láșp trĂŹnh, cĂĄc thĂ nh pháș§n của ngĂŽn ngữ C, cáș„u trĂșc ráșœ nhĂĄnh, vĂČng láș·p, hĂ m, máșŁng, chuá»i, con trá» vĂ táșp tin. NĂł cung cáș„p kiáșżn thức từ lĂœ thuyáșżt Äáșżn thá»±c hĂ nh vá»i nhiá»u bĂ i táșp nháș±m giĂșp há»c viĂȘn hiá»u vĂ ĂĄp dỄng ÄÆ°á»Łc cĂĄc khĂĄi niá»m trong láșp trĂŹnh C. GiĂĄo trĂŹnh cĆ©ng hÆ°á»ng dáș«n viá»c lĂ m quen vá»i cĂŽng cỄ Borland C trong láșp trĂŹnh.C++ can ban(dung thu vien iostream)
C++ can ban(dung thu vien iostream)Nguyá»
n PhỄng
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» ngĂŽn ngữ láșp trĂŹnh C++, từ khĂĄi niá»m cÆĄ báșŁn Äáșżn nĂąng cao, bao gá»m cáș„u trĂșc chÆ°ÆĄng trĂŹnh, cĂĄc kiá»u dữ liá»u vĂ cĂĄch khai bĂĄo biáșżn. NĂł giá»i thiá»u cĂș phĂĄp của chÆ°ÆĄng trĂŹnh Äáș§u tiĂȘn báș±ng C++ vĂ giáșŁi thĂch Ăœ nghÄ©a của từng pháș§n trong mĂŁ nguá»n. TĂ i liá»u cĆ©ng Äá» cáșp Äáșżn cĂĄc quy táșŻc Äáș·t tĂȘn biáșżn, cĂĄch sá» dỄng cĂĄc loáșĄi dữ liá»u cÆĄ báșŁn vĂ nhĂłm cĂĄc biáșżn theo kiá»u dữ liá»u.Thdc 08
Thdc 08Nguyá»
n PhỄng
Ìę
TĂ i liá»u trĂŹnh bĂ y vá» cĂĄc cĂąu lá»nh cÆĄ báșŁn trong láșp trĂŹnh C, bao gá»m lá»nh if, switch, for, while, do...while, goto, break, continue vĂ return. Má»i lá»nh cĂł cĂș phĂĄp vĂ vĂ dỄ cỄ thá» Äá» minh há»a cĂĄch sá» dỄng chĂșng trong viá»c láșp trĂŹnh. CĂĄc khá»i lá»nh vĂ cáș„u trĂșc kiá»m soĂĄt luá»ng của chÆ°ÆĄng trĂŹnh ÄÆ°á»Łc giáșŁi thĂch rĂ” rĂ ng nháș±m giĂșp ngÆ°á»i há»c náșŻm vững kiáșżn thức vá» láșp trĂŹnh cÆĄ báșŁn.Thdc 07
Thdc 07Nguyá»
n PhỄng
Ìę
TĂ i liá»u cung cáș„p kiáșżn thức cÆĄ báșŁn vá» láșp trĂŹnh ngĂŽn ngữ C, bao gá»m cĂĄc kiá»u dữ liá»u cÆĄ sá», háș±ng vĂ biáșżn, cĂčng vá»i cĂĄc quy táșŻc vĂ phĂ©p toĂĄn cÆĄ báșŁn. NĂł cĆ©ng giá»i thiá»u cĂĄc hĂ m nháșp xuáș„t dữ liá»u vĂ cĂĄc phĂ©p toĂĄn nhÆ° sá» há»c, thao tĂĄc bit, vĂ phĂ©p toĂĄn Äiá»u kiá»n. TĂ i liá»u cá»t lĂ”i cho viá»c há»c láșp trĂŹnh mĂĄy tĂnh vĂ giáșŁi quyáșżt bĂ i toĂĄn thuáșt toĂĄn.Thdc 06
Thdc 06Nguyá»
n PhỄng
Ìę
TĂ i liá»u trĂŹnh bĂ y khĂĄi niá»m vĂ quy trĂŹnh giáșŁi quyáșżt bĂ i toĂĄn trong tin há»c, bao gá»m cĂĄc bÆ°á»c nhÆ° xĂĄc Äá»nh váș„n Äá», lá»±a chá»n phÆ°ÆĄng phĂĄp, xĂąy dá»±ng thuáșt toĂĄn vĂ cĂ i Äáș·t chÆ°ÆĄng trĂŹnh. NĂł cĆ©ng mĂŽ táșŁ cĂĄc khĂĄi niá»m vá» thuáșt toĂĄn, cáș„u trĂșc dữ liá»u, vĂ cĂĄc phÆ°ÆĄng phĂĄp biá»u diá»
n thuáșt toĂĄn. Cuá»i cĂčng, tĂ i liá»u Äá» cáșp Äáșżn quy trĂŹnh phĂĄt triá»n pháș§n má»m vĂ cĂĄc tiĂȘu chuáș©n của chÆ°ÆĄng trĂŹnh.Ad
04 hang ma tran
- 1. BĂI 4
- 2. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn
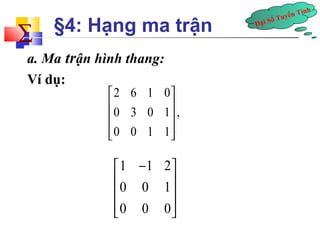
- 3. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn ïź VĂ dỄ: 12 12 1 2 A = 2 4 1 2 3 4 4 6 8 3 5 7 9 A Ă© Ă© Ăč Ăč = ĂȘ Ăș ĂȘ Ă« Ă» Ăș Ăș ĂȘĂ« 24 12 A = 2 4 4 8 Ă© Ăč ĂȘ Ăș Ă« Ă» 234 123 A = 2 3 4 4 6 5 7 9 Ă© Ăč ĂȘ Ăș ĂȘ ĂȘĂ« ĂșĂ»
- 4. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn
- 5. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn
- 6. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn 0 0 0 0 0 0 0 0 0 0 0 0 O Ă© Ăč = ĂȘ Ăș ĂȘ Ăș ĂȘĂ« ĂșĂ» 2 [ ] 1 A = 0 24 13 0 0 0 0 A Ă© Ăč = ĂȘ Ăș Ă« Ă»
- 7. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn a b c d A Ă© Ăč = ĂȘ Ăș Ă« x y z t Ă»
- 8. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn a b c Ă© Ăč = ĂȘ Ăș ĂȘ Ăș ĂȘĂ« ĂșĂ» A x y z u v w A cĂł duy nháș„t 1 Äá»nh thức con cáș„p 3 vĂ ÄĂł lĂ Äá»nh thức con cĂł cáș„p lá»n nháș„t
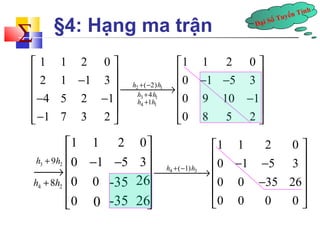
- 9. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn PhÆ°ÆĄng phĂĄp tĂŹm háșĄng của ma tráșn: a. Ma tráșn hĂŹnh thang: lĂ ma tráșn cáș„p mxn thá»a cĂĄc Äiá»u kiá»n sau: 1. CĂĄc hĂ ng báș±ng khĂŽng (náșżu cĂł) náș±m á» dÆ°á»i cĂĄc hĂ ng khĂĄc khĂŽng. 2. Pháș§n tá» khĂĄc 0 Äáș§u tiĂȘn của hĂ ng dÆ°á»i náș±m vá» bĂȘn pháșŁi pháș§n tá» khĂĄc 0 Äáș§u tiĂȘn của hĂ ng trĂȘn.
- 10. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn a. Ma tráșn hĂŹnh thang: VĂ dỄ: 2 6 1 0 0 3 0 1 , 0 0 1 1 Ă© Ăč ĂȘ Ăș ĂȘ Ăș ĂȘĂ« ĂșĂ» 1 1 2 0 0 1 0 0 0 Ă© - Ăč ĂȘ Ăș ĂȘ Ăș ĂȘĂ« ĂșĂ»
- 11. TĂnh Ă„ §4: HáșĄng ma tráșn Tuyáșżn ÄáșĄi Sá» b.CĂĄc phĂ©p biáșżn Äá»i sÆĄ cáș„p trĂȘn ma tráșn: 1.NhĂąn má»t sá» khĂĄc khĂŽng vá»i má»t hĂ ng (cá»t) của ma tráșn. KĂœ Ahiá»u: ŸhŸi =lŸhiÂźB 2.Äá»i chá» hai hĂ ng (cá»t) của ma tráșn. KĂœ hiá»u: A ÂŸÂŸÂŸÂź hi « hj B 3.Cá»ng vĂ o má»t hĂ ng (cá»t) vá»i má»t hĂ ng (cá»t) khĂĄc ÄĂŁ nhĂąn thĂȘm má»t sá» khĂĄc khĂŽng. A ŸKĂœ hŸi = hiá»u: hiŸ+ l hŸjÂź B
- 12. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn
- 13. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn c. Qui táșŻc thá»±c hĂ nh tĂŹm háșĄng của ma tráșn
- 14. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn biáșżn Äá»i sÆĄ cáș„p A B (cĂł dáșĄng hĂŹnh thang) Khi ÄĂł: r(A) = r(B)(sá» dĂČng khĂĄc khĂŽng của B)
- 15. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn VĂ dỄ: TĂŹm háșĄng ma tráșn: 1 3 2 0 1 4 0 3 3 4 0 1 0 0 5 8 9 1 0 0 0 0 0 0 0 0 0 0 0 0 A Ă© - Ăč ĂȘ Ăș ĂȘ Ăș = ĂȘ - Ăș ĂȘ Ăș ĂȘ Ăș ĂȘĂ« ĂșĂ» Ăr(A) = 3
- 16. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn ïź VĂ dỄ: TĂŹm háșĄng ma tráșn -5=-1+(-2)2 1 1 2 0 1 1 2 0 2 1 1 3 0 4 5 2 1 1 7 3 2 Ă© Ăč Ă© Ăč ĂȘ ĂȘ - Ăș ĂȘ ĂșÂŸÂŸÂŸÂŸÂźĂȘ -1? -5 3 Ăș h 2 + ( - 2) h 1 Ăș ĂȘ- - Ăș h + 4h 3 1 0 ĂȘ 9 10 -1 Ăș ĂȘ- Ăș h +1h 4 1 Ă« Ă» 0 ĂȘ Ăș Ă« 8 5 2 Ă» ?=1+(-2)1=-1 Ta lĂ m cho pháș§n dÆ°á»i ÄÆ°á»ng chĂ©o chĂnh = 0. Ta láș·p láșĄi nhÆ° trĂȘn cho pháș§n ma tráșn nĂ y
- 17. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn 1 1 2 0 1 1 2 0 2 1 1 3 0 1 5 3 4 5 2 1 0 9 10 1 1 7 3 2 0 8 5 2 Ă© Ăč Ă© Ăč ĂȘ ĂȘ - Ăș ĂȘ ĂșÂŸÂŸÂŸÂŸÂźĂȘ - - Ăș h 2 + ( - 2) h 1 Ăș ĂȘ- - Ăș h 3 + 4 h 1 ĂȘ - Ăș ĂȘ- Ăș h 4 + 1 h 1 ĂȘ Ăș Ă« Ă» Ă« Ă» 1 1 2 0 0 1 5 3 0 0 0 Ă© Ăč ĂȘ - - Ăș ÂŸÂŸÂźĂȘ Ăș ĂȘ Ăș ĂȘ Ăș Ă« Ă» 3 2 h + 9h -35 26 0 4 2 h + 8h -35 26 Ă© Ăč ĂȘ Ăș ÂŸÂŸÂŸÂŸÂźĂȘ - - 4 ( 1) 3 Ăș 1 1 2 0 0 1 5 3 0 0 35 26 0 0 0 0 h + - h ĂȘ - Ăș ĂȘ Ăș Ă« Ă»
- 18. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn ïź BĂ i táșp: TĂŹm háșĄng của ma tráșn sau: h3 - 4h1 Ă© 1 2 - 1 0 Ăč ĂȘ ĂȘ 2 3 0 5 Ăș Ăș ĂȘ 4 1 2 0 Ăș ĂȘ- Ă« 3 0 5 7 Ăș Ă» Ă© - Ăč ĂȘ Ăș 1 2 1 0 0 0 0 ÂŸÂŸÂźĂȘ Ăș ĂȘ Ăș ĂȘ Ăș Ă« Ă» 2 1 h - 2h 4 1 h + 3h -1 2 5
- 19. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn ïź VĂ dỄ: Biá»n luáșn theo m háșĄng của ma tráșn sau: 1 5 6 0 4 7 0 0 A Ă© Ăč = ĂȘ Ăș ĂȘ Ăș ĂȘĂ« m ĂșĂ» ï r(A) = 2 m = 0 m Âč 0 ï r(A) = 3
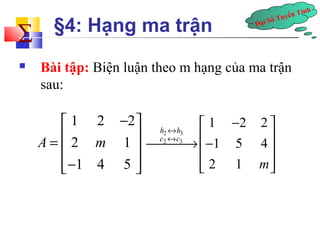
- 20. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn ïź BĂ i táșp: Biá»n luáșn theo m háșĄng của ma tráșn sau: Ă© 1 2 - 2 Ăč = ĂȘ ĂȘ 2 1 Ăș Ăș ĂȘĂ«- 1 4 5 ĂșĂ» A m 2 3 2 3 1 2 2 1 5 4 2 1 h h c c m « « Ă© - Ăč ÂŸÂŸÂŸÂźĂȘ- Ăș ĂȘ Ăș ĂȘĂ« ĂșĂ»
- 21. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn Ă© 1 - 2 2 Ăč Âź ... ÂźĂȘ ĂȘ 0 3 6 Ăș Ăș ĂȘĂ« 0 0 3m - 42 ĂșĂ» ï r(A) = 2 3m- 42 = 0Ăm =14 3m- 42 Âč 0Ăm Âč 14 ï r(A) = 3
- 22. ÄáșĄi Sá» Tuyáșżn TĂnh Ă„ §4: HáșĄng ma tráșn ïź BĂ i táșp: Biá»n luáșn theo a, b háșĄng của ma tráșn sau: Ă© 1 2 0 - 1 Ăč ĂȘ ĂȘ 2 1 3 0 Ăș = Ăș ĂȘ 0 3 Ăș ĂȘ Ă« 3 3 3 - 1 Ăș Ă» A a b ŸhŸ3«Ÿh4Âź