01 ma tran
- 1. B?I 1 W a F ¨¦ ¨´ ¨º ¨º j ? v ¨² ¨² ¨º? e x d ? ¨²
- 2. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n ??nh ngh?a: Ma tr?n c? mxn tr¨ºn R l¨¤ m?t b?ng g?m m.n s? th?c ???c vi?t th¨¤nh m h¨¤ng v¨¤ n c?t nh? sau: a a a a a a ¨¦ ¨º 11 12 1 ¨´ ¨² = ¨º 21 22 2 ¨² ¨º ¨² ¨º ¨º? a a a ¨² 1 2 ¨²? ... ... A ... ... ... ... ... n n m m mn K¨ª hi?u: A = [aij]mxn T?p h?p t?t c? c¨¢c ma tr?n c? mxn tr¨ºn R ???c k? hi?u l¨¤ Mmxn(R)
- 3. ??i S? Tuy?n T¨ªnh ? a a a a a a a a ¨¦ ¨º 11 12 1 j 1 n ¨´ ¨² ¨º 21 22 2 j 2 n ¨² ¨º ¨² ¨º ¨º a a a a ¨² i 1 i 2 ij in ¨² ¨º ¨² ¨º ¨² ¨º? a a a a 1 2 ¨²? ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... m m mj mn H¨¤ng th? nh?t a11 a22 a33 ¡ g?i l¨¤ ???ng ch¨¦o ch¨ªnh (m = n) H¨¤ng th? i C?t th? 2 C?t th? j aij: Ph?n t? n?m ? h¨¤ng i c?t j aij mxn: g?i l¨¤ c?p c?a ma tr?n ¡ì1: Ma Tr?n
- 4. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n V¨ª d?: 1 0 2 3 1.5 5 A ¨¦ ¨´ = ¨º ¨² ?- ? 2 8 6 2 9 0 0 7 2 B ¨¦ - ¨´ = ¨º ¨² ¨º ¨² 2x3 ¨º? - - ¨²? 3x3 21 ???ng ch¨¦o ch¨ªnh a
- 5. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n * Khi m = n (s? h¨¤ng = s? c?t) ta n¨®i A l¨¤ ma tr?n vu?ng c?p n. T?p h?p t?t c? c¨¢c ma tr?n vu?ng c?p n ???c k? hi?u Mn. V¨ª d?: 0 7 8 1 3 ¨¦ ¨´ ¨¦ ¨´ ¨º ¨º- ¨² ; 4 - 2 0 ¨² ? 2 7 ? ¨º ¨² ¨º ? 5 0 2 ? ¨² Ma tr?n vu?ng c?p 2 Ma tr?n vu?ng c?p 3
- 6. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n C¨¢c ma tr?n ??c bi?t: 1. Ma tr?n kh?ng: aij = 0,"i, j. (t?t c? c¨¢c ph?n t? ??u = 0) V¨ª d?: 0 0 0 0 0 0 O ¨¦ ¨´ = ¨º ¨² ? ?
- 7. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? C¨¢c ma tr?n ??c bi?t: 2. Ma tr?n ch¨¦o: l¨¤ ma tr?n vu?ng c¨®: aij = 0,"i ? j. (c¨¢c ph?n t? ngo¨¤i ???ng ch¨¦o ch¨ªnh = 0) V¨ª d?: 2 0 0 0 4 0 0 0 9 ¨¦ ¨´ ¨º ¨² ¨º ¨² ¨º? ¨²? ¨¦ ¨º 11 ¨´ ¨² ¨º ¨² ¨º ¨² ¨º ¨² ? ? 0 ... 0 0 ... 0 22 ... ... ... ... 0 0 ... nn a a a
- 8. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n C¨¢c ma tr?n ??c bi?t: 3. Ma tr?n ??n v?: l¨¤ ma tr?n ch¨¦o c¨®: aii =1,"i =1, 2,..., n. K? hi?u: I, In. V¨ª d?: 2 3 1 0 ... 0 1 0 0 1 0 0 1 ... 0 , 0 1 0 , 0 1 .. .. ... .. 0 0 1 0 0 ... 1 n I I I ¨¦ ¨´ ¨¦ ¨´ ¨º ¨² ¨¦ ¨´ ¨º ¨² ¨º ¨² = ¨º ¨² = ¨º ¨² = ? ? ¨º ¨² ¨º? ¨²? ¨º ¨² ? ?
- 9. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n C¨¢c ma tr?n ??c bi?t: 4. Ma tr?n tam gi¨¢c: l¨¤ ma tr?n vu?ng c¨® aij = 0,"i > j. (tam gi¨¢c tr¨ºn) 0, . ij a = "i < j (tam gi¨¢c d??i) V¨ª d?: 1 2 5 4 ¨¦ ¨´ ¨º ¨º 0 3 - 1 0 ¨² ¨² ¨º 0 0 2 6 ¨² ¨º ? 0 0 0 9 ¨² ? 2 0 0 0 7 1 0 0 0 8 2 0 2 9 1 5 ¨¦ ¨´ ¨º ¨² ¨º ¨² ¨º ¨² ¨º ¨² ? ? MT tam gi¨¢c tr¨ºn MT tam gi¨¢c d??i
- 10. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n C¨¢c ma tr?n ??c bi?t: 5. Ma tr?n c?t:l¨¤ ma tr?n c¨® n=1. Ma tr?n c?t c¨® d?ng: a a ¨¦ ¨º 11 ¨´ ¨² ¨º 21 ¨² ¨º .. ¨² ¨º a ¨² ? m 1 ?
- 11. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? C¨¢c ma tr?n ??c bi?t: 6. Ma tr?n h¨¤ng: l¨¤ ma tr?n c¨® m=1. Ma tr?n h¨¤ng c¨® d?ng: [ ] 11 12 1 ... n a a a
- 12. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? C¨¢c ma tr?n ??c bi?t: 7. Ma tr?n b?ng nhau: = ¨¦? ¨´? = ¨¦? ¨´? = ? ij = ij " m n m n A a b B a b i j 8. Ma tr?n chuy?n v?: cho ma tr?n A=[aij]mxn, ma tr?n chuy?n v? c?a ma tr?n A k? hi?u AT v¨¤ x¨¢c ??nh AT=[bij]nxm v?i bij=aji v?i m?i i,j. (chuy?n h¨¤ng th¨¤nh c?t) ij ij , , . ? ?
- 13. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n D?ng c?a ma tr?n chuy?n v?: a a a a a a a a a a a a ¨¦ ¨º 11 12 1 n ¨´ ¨¦ 11 21 m 1 ¨´ ¨² ¨º ¨² = ¨º 21 22 2 n ¨² ? T = ¨º 12 22 m 2 ¨² ¨º ¨² ¨º ¨² ¨º ¨² ¨º ¨² ¨º? ¨²? ¨º? ¨²? A A a a a a a a m 1 m 2 mn m n 1 n 2 n nm n m V¨ª d?: ... ... ... ... .. .. ... .. .. .. ... .. ... ... ? ? 2 3 3 2 1 6 1 2 5 2 7 6 7 9 ? 5 9 ? ¨¦ ¨´ ¨¦ ¨´ ¨º ¨² = ¨º ¨² ? = ¨º ¨² ? ? ¨º ¨² ? ? A AT
- 14. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n * Khi A = AT th¨¬ A ???c g?i l¨¤ ma tr?n ??i x?ng. V¨ª d?: 1 2 3 2 0 5 3 5 1 ¨¦ ¨´ = = ¨º ¨² ¨º ¨² ¨º? - ¨²? A AT
- 15. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n * Khi A = -AT th¨¬ A ???c g?i l¨¤ ma tr?n ph?n ??i x?ng. V¨ª d?: ¨¦ 0 1 4 ¨´ ¨¦ 0 - 1 - 4 ¨´ = ¨º- 1 0 - 3 ¨² ? T = ¨º 1 0 3 ¨² ¨º ¨² ¨º ¨² ¨º?- 4 3 0 ¨²? ¨º? 4 - 3 0 ¨²? = - A A T A A
- 16. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n C¨¢c ph¨¦p to¨¢n tr¨ºn ma tr?n: 1. Ph¨¦p c?ng hai ma tr?n: ¨¦? a + b = a + b ij ¨´? ¨¦? ¨´? ¨¦? ¨´? m ? n ij m ? n ij ij m ? n (c?ng theo t?ng v? tr¨ª t??ng ?ng) V¨ª d?: 0 1 2 3 3 5 2 4 4 2 1 5 1+ 0=11 2+3=55 ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ ¨º- ¨² ¨º ¨² ¨º ¨² ¨º ¨² + ¨º - ¨² = ¨º -1 1 ¨² ¨º? - ¨²? ¨º? ¨²? ¨º? 5 3 ¨²?
- 17. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n C¨¢c t¨ªnh ch?t: Gi? s? A,B,C,O l¨¤ c¨¢c ma tr?n c¨´ng c?p, khi ?¨®: i ) A + B = B + A ii ) A + O = A + O = A iii ) A + ( B + C ) = ( A + B ) + C
- 18. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n C¨¢c ph¨¦p to¨¢n tr¨ºn ma tr?n: 2. Ph¨¦p nh?n m?t s? v?i m?t ma tr?n: l ¨¦? a ¨´? = ¨¦? l . a , l ? R. ij ¨´? m ? n ij m ? n (c¨¢c ph?n t? c?a ma tr?n ??u ???c nh?n cho l ) V¨ª d?: 3 ¨¦ - 2 0 ¨´ ¨¦ ¨´ ¨º ¨º 7 4 5 ¨² ¨² = ¨º ¨² ¨º ¨² ¨º? 0 - 2 1 ¨²? ¨º? ¨²? 2.3=66 2.(-2)=-4 -2 -0 14 2.0=0 8 10 0 -4 2
- 19. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? C¨¢c t¨ªnh ch?t: "a ,b ?R,"A, B l¨¤ hai ma tr?n c¨´ng c?p, khi ?¨® i ) a ( A + B ) = a A + a B ii ) ( a + b ) A = a A + b A iii ) a ( b A ) = ( ab ) A iv ) 1 A = A Sinh vi¨ºn t? ki?m tra.
- 20. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n ? Ch¨² ?: A- B = A+ (-1)B 1 3 6 5 1 3 6 5 ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ ¨º ¨² - ¨º ¨² = ¨º + ( - 1) ? 4 5 ? ? 1 3 ? ? 4 5 ¨² ¨º ? ? 1 3 ¨² ? ¨¦ 1 3 ¨´ ¨¦- 6 - 5 ¨´ ¨¦- 5 - 2 ¨´ = ¨º + = ? 4 5 ¨² ¨º ¨² ¨º ¨² ? ?- 1 - 3 ? ? 3 2 ? ? Nh?n x¨¦t: tr? 2 ma tr?n l¨¤ tr? theo v? tr¨ª t??ng ?ng
- 21. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n C¨¢c ph¨¦p to¨¢n tr¨ºn ma tr?n: 3. Ph¨¦p nh?n hai ma tr?n: Cho hai ma tr?n m? p ; p?n , A B [ ] ? ? ? = m p p n ij m n A B c Khi ?¨® ma tr?n g?i l¨¤ t¨ªch c?a hai ma tr?n A, B. Trong ?¨®: 1 1 2 2 ... , 1, ; 1, . ij i j i j ip pj c = a b + a b + + a b "i = m j = n i1 a i2 a ip a H¨¤ng th? i c?a ma tr?n A. 1 j b 2 j b pj b C?t th? j c?a ma tr?n B. ij c Nh? v?y = h¨¤ng th? i c?a ma tr?n A nh?n t??ng ?ng v?i c?t th? j c?a ma tr?n B r?i c?ng l?i.
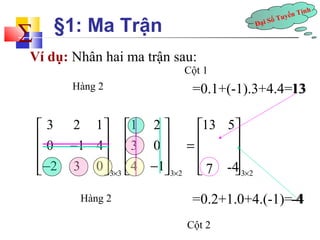
- 22. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? V¨ª d?: Nh?n hai ma tr?n sau: 3. 1 2 3 2 1 0 =3.2+2.0+1.(-1)=55 -1 3 2 1 1 2 0 1 4 3 0 2 3 0 4 1 ? ? ? ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ ¨º - ¨² ¨º .3 ¨² ¨º ¨² ¨º ¨² = ¨º ¨² ¨º ¨² ¨º?- ¨²? ¨º? - ¨²? ¨º? ¨²? 3 3 3 2 3 2 +2 +1 .4 =1133 = Ch¨² ?: h¨¤ng 1 nh?n c?t 2 vi?t v¨¤o v? tr¨ª 12 c s? c?t c?a A= s? h¨¤ng c?a B
- 23. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n V¨ª d?: Nh?n hai ma tr?n sau: C?t 1 H¨¤ng 2 =0.1+(-1).3+4.4=13 3 2 1 1 2 13 5 0 1 4 3 0 2 3 0 4 1 ? ? ? ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ ¨º ¨º - ¨² ¨º ¨² ¨º ¨² ¨² ¨º ¨² = ¨º ¨² ¨º?- ¨²? ¨º? - ¨²? ¨º? 7 -4 ¨²? 3 3 3 2 3 2 H¨¤ng 2 =0.2+1.0+4.(-1)=--44 C?t 2
- 24. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n ? Ch¨² ?: Ph¨¦p nh?n 2 ma tr?n kh?ng giao ho¨¢n 1 4 5 2 ¨¦ 3 - 1 ¨´ ¨º ¨² ? 4 0 ? 1 4 3 1 4 1 1 2 10 5 2 4 6 3 1 2 0 9 5 AB BA ¨¦ - ¨´ ¨º ¨² ¨¦ ¨´ = ¨º ¨² = ? ? ¨¦ ¨´ = ¨º ¨² = ? ? ¨¦ - ? - ¨´ ¨º ¨² ? ? ¨¦- ¨´ ¨º ¨² ? ? ? ? V¨ª d?:
- 25. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n ? V¨ª d?: 1 5 7 1 0 0 1 5 7 8 4 2 0 1 0 8 4 2 3 1 0 0 0 1 3 1 0 ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ = ¨º ¨² ¨º ¨² = ¨º ¨² = ¨º ¨² ¨º ¨² ¨º ¨² ¨º? ¨²? ¨º? ¨²? ¨º? ¨²? AI A 1 0 0 1 5 7 1 5 7 0 1 0 8 4 2 8 4 2 0 0 1 3 1 0 3 1 0 ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ = ¨º ¨² ¨º ¨² = ¨º ¨² = ¨º ¨² ¨º ¨² ¨º ¨² ¨º? ¨²? ¨º? ¨²? ¨º? ¨²? IA A
- 26. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? C¨¢c t¨ªnh ch?t: Ta gi? s? c¨¢c ma tr?n c¨® c?p ph¨´ h?p ?? t?n t?i ma tr?n t¨ªch i A BC = AB C ii A B + C = AB + AC iii A + B C = AC + BC iv " k ? R k AB = kA B = A kB v AI = A IA = A ) ( ) ( ) ) ( ) ) ( ) ) , ( ) ( ) ( ) ) ( )
- 27. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? C¨¢c t¨ªnh ch?t: T T T i ) ( A + B ) = A + B ii ) ( kA ) T = kA T , " k ? R iii ) ( AB ) T = B T A T Sinh vi¨ºn t? ki?m tra.
- 28. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? ?a th?c c?a ma tr?n : Cho ?a th?c 0 1 ( ) n n ... n n P x = a x + a x - + + a v¨¤ ma tr?n vu?ng Khi ?¨®: A = [aij ]n 1 P ( A ) = a A n + a A n - 1 + ... + a I n 0 1 n n n I (trong ?¨® l¨¤ ma tr?n ??n v? c¨´ng c?p v?i ma tr?n A)
- 29. T¨ªnh ? ¡ì1: Ma Tr?n Tuy?n ??i S? V¨ª d?: Cho 2 P2 (x) = x -3x + 5 v¨¤ ma tr?n 1 2 A ¨¦ ¨´ = ¨º ? 0 - 3 ¨² ? Khi ?¨®: 2 P ( A ) = A - 3 A+ 5 I 2 2 2 1 2 1 2 1 0 ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ = ¨º ¨² - 3 ¨º ¨² + 5 ¨º ¨² ? 0 - 3 ? ? 0 - 3 ? ? 0 1 ?
- 30. T¨ªnh ? ¡ì1: Ma Tr?n S? Tuy?n ??i ¨¦ 3 5 ¨´ V¨ª d?: Cho f (x) = x2 + 3x -5 v¨¤ A = ¨º ? 1 4 ¨² T¨ªnh ? f(A)? ? Ta c¨®: 2 2 f ( A ) = A + 3 A- 5 I 2 3 5 3 5 1 0 ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ = ¨º ¨² + 3 1 4 ¨º 1 4 ¨² - 5 ¨º ¨² ? ? ? ? ? 0 1 ? ¨¦ 3 5 ¨´ ¨¦ 3 5 ¨´ ¨¦ 9 15 ¨´ ¨¦- 5 0 ¨´ = ¨º + 1 4 ¨² ¨º 1 4 ¨² ¨º 3 12 ¨² - ¨º ? ? ? ? ? ? ? 0 - 5 ¨² ? 144424443 14 35 4 15 18 50 7 21 3 7 10 28 ¨¦ ¨´ ¨¦ ¨´ ¨¦ ¨´ = ¨º ¨² + ¨º ¨² = ¨º ¨² AA ? ? ? ? ? ?
- 31. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n ? B¨¤i t?p: Cho 2 0 0 2 0 ¨¦ ¨´ ¨¦ ¨´ = ¨º - ¨² = ¨º - ¨² ¨º ¨² ¨º ¨² ¨º? - ¨²? ¨º? ¨²? A B 3 1 0 ; 1 3 4 2 5 4 5 ? T¨ªnh AB; A2 ; AT A; AB -3B.
- 32. ??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n ? B¨¤i t?p: Cho v¨¤ ma tr?n T¨ªnh f(A) =? f (x) = x2 + 3x - 4 1 2 3 0 3 4 0 0 2 A ¨¦ ¨´ = ¨º ¨² ¨º ¨² ¨º? ¨²?
![??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n
??nh ngh?a: Ma tr?n c? mxn tr¨ºn R l¨¤ m?t b?ng
g?m m.n s? th?c ???c vi?t th¨¤nh m h¨¤ng v¨¤ n c?t
nh? sau:
a a a
a a a
¨¦ ¨º 11 12 1
¨´
¨²
= ¨º 21 22 2
¨² ¨º ¨²
¨º ¨º? a a a
¨²
1 2
¨²?
...
...
A
... ... ... ...
...
n
n
m m mn
K¨ª hi?u: A = [aij]mxn
T?p h?p t?t c? c¨¢c ma tr?n c? mxn tr¨ºn R ???c k?
hi?u l¨¤ Mmxn(R)](https://image.slidesharecdn.com/01matran-141007084741-conversion-gate01/85/01-ma-tran-2-320.jpg)








![T¨ªnh ?
¡ì1: Ma Tr?n
Tuy?n ??i S? C¨¢c ma tr?n ??c bi?t:
6. Ma tr?n h¨¤ng: l¨¤ ma tr?n c¨® m=1.
Ma tr?n h¨¤ng c¨® d?ng:
[ ] 11 12 1 ... n a a a](https://image.slidesharecdn.com/01matran-141007084741-conversion-gate01/85/01-ma-tran-11-320.jpg)
![T¨ªnh ?
¡ì1: Ma Tr?n
Tuy?n ??i S? C¨¢c ma tr?n ??c bi?t:
7. Ma tr?n b?ng nhau:
= ¨¦? ¨´? = ¨¦? ¨´? = ? ij = ij " m n m n
A a b B a b i j
8. Ma tr?n chuy?n v?: cho ma tr?n A=[aij]mxn,
ma tr?n chuy?n v? c?a ma tr?n A k? hi?u AT
v¨¤ x¨¢c ??nh AT=[bij]nxm v?i bij=aji v?i m?i
i,j. (chuy?n h¨¤ng th¨¤nh c?t)
ij ij , , .
? ?](https://image.slidesharecdn.com/01matran-141007084741-conversion-gate01/85/01-ma-tran-12-320.jpg)








![??i S? Tuy?n T¨ªnh ? ¡ì1: Ma Tr?n
C¨¢c ph¨¦p to¨¢n tr¨ºn ma tr?n:
3. Ph¨¦p nh?n hai ma tr?n: Cho hai ma tr?n
m? p ; p?n , A B
[ ] ? ? ? = m p p n ij m n A B c
Khi ?¨® ma tr?n g?i l¨¤ t¨ªch c?a
hai ma tr?n A, B. Trong ?¨®:
1 1 2 2 ... , 1, ; 1, . ij i j i j ip pj c = a b + a b + + a b "i = m j = n
i1 a i2 a ip a H¨¤ng th? i c?a ma tr?n A.
1 j b 2 j b pj b C?t th? j c?a ma tr?n B.
ij c
Nh? v?y = h¨¤ng th? i c?a ma tr?n A nh?n t??ng ?ng
v?i c?t th? j c?a ma tr?n B r?i c?ng l?i.](https://image.slidesharecdn.com/01matran-141007084741-conversion-gate01/85/01-ma-tran-21-320.jpg)





![T¨ªnh ?
¡ì1: Ma Tr?n
Tuy?n ??i S? ?a th?c c?a ma tr?n :
Cho ?a th?c
0 1 ( ) n n ...
n n P x = a x + a x - + + a
v¨¤ ma tr?n vu?ng
Khi ?¨®:
A = [aij ]n
1
P ( A ) = a A n + a A n - 1
+ ...
+ a I
n 0 1 n n n I
(trong ?¨® l¨¤ ma tr?n ??n v? c¨´ng c?p v?i ma tr?n A)](https://image.slidesharecdn.com/01matran-141007084741-conversion-gate01/85/01-ma-tran-28-320.jpg)









































































