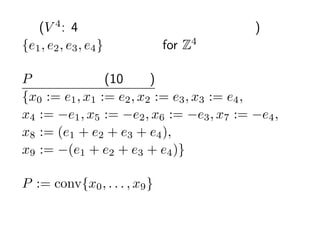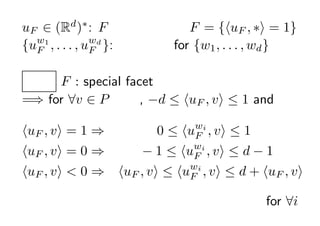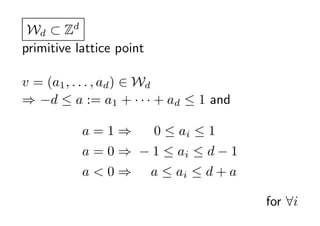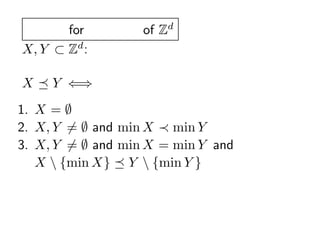120919 kyushu
- 1. 2012 ─Ļ 9 į┬ 19, 20 ╚š źšźĪź╬ČÓ├µ╠Õż╬ĘųŅÉ└Ēšō ߬ĖĘ┬}Åį観@┤¾č¦ ĮU£gŪķł¾č¦▓┐ ū¶╠┘ ═ž Š┼ų▌┤¾č¦ź▐ź╣?źšź®źó?źżź¾ź└ź╣ź╚źĻ蹊┐╦∙Č╠Ų┌╣▓═¼čąŠ┐ĪĖč¦┴Ģ└Ēšōż╦ż¬ż▒żļĮM║Žż╗└ĒšōĪ╣
- 2. 1 ─┐┤╬ Į±╚š ? ź╚®`źĻź├ź»?źšźĪź╬ČÓśö╠Õ ? źšźĪź╬ČÓ├µ╠Õ ? Ą═┤╬į¬ (Ī▄ 4) ż╬ĘųŅÉ ? ź╚®`źĻź├ź»╔Ł└Ēšō
- 3. ├„╚š ? Ė▀┤╬į¬ (Ī▌ 5) ż╬ĘųŅÉ ? ?bro ż╬źóźļź┤źĻź║źÓ SFP ? 2 ┤╬į¬żŪ SFP īgč▌
- 4. 2 źšźĪź╬ČÓśö╠Õ X: ź│ź¾źčź»ź╚č}╦žČÓśö╠Õ X: źšźĪź╬ ? ?KX = c1 (X): ample (š²) # {d ┤╬į¬źšźĪź╬ČÓśö╠Õż╬ēõą╬ŅÉ } < +Ī▐ d = 2: źŪźļź┌ź├ź─ź®Ū·├µ P2 ż╬ n ĄŃ▒¼░k (n Ī▄ 8) or P1 Ī┴ P1 d = 3: Iskovskih (1978), Mori-Mukai (1981)
- 5. Minimal Model Program input output X : ┤·╩²ČÓśö╠Õ Ī· MMP Ī· (1) śOąĪźŌźŪźļ (2) ╔ŁźšźĪźżźą®`┐šķg ”š:XĪ·Y d = dim X > dim Y ”š?1 (p): źšźĪź╬ČÓśö╠Õ (p Ī╩ Y )
- 6. 3 ź╚®`źĻź├ź»ČÓśö╠Õ Ī┴ d T := (C ) : ┤·╩²Ą─ź╚®`źķź╣ T ? X (open dense): ź╚®`źĻź├ź»ČÓśö╠Õ ź╚®`źĻź├ź»ČÓśö╠Õ ? ╔╚ (ČÓ├µ╠Õ) ╔╚ (in R ? Z ) ż¼ X T ż╬źŪ®`ź┐ż“│ųż├żŲżżżļ d d
- 7. r r r r r r r r r r r r r r pt. r r r r r r r u u rrCĪ┴ r r r e r r r e rr ĆĆ e (CĪ┴ )2@@ u @ r r r r r r ĆrĆ r Ć eu @@ @ r r r r r r r r r r r r r r ╔╚ Ī¹Ī· ź╚®`źĻź├ź»ČÓśö╠Õ
- 8. 4 źšźĪź╬ČÓ├µ╠Õ ź╚®`źĻź├ź»?źšźĪź╬ČÓśö╠Õ ? źšźĪź╬ČÓ├µ╠Õ P ? Rd ? Zd : ═╣ČÓ├µ╠Õ (ĒöĄŃ╝»║Ž ? Zd ) P : źšźĪź╬ČÓ├µ╠Õ ?? ? 1. P Ī╔ Z = {0} d 2. ╚╬ęŌż╬ facet F ? P ż╦īØżĘżŲ, F ż╬ĒöĄŃ╝»║ŽżŽ Zd ż╬╗∙Ąūż“ż╩ż╣
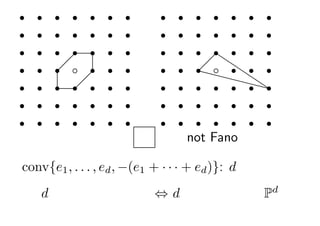
- 9. r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r?b r ? r r r r ??? r r ?b r r? ?? ? r r r? r ?r r r r r ???r r r r r? r r r r r r r r r r r r r r r r r r r r r r r r r r r r źšźĪź╬ČÓ├µ╠Õ └² not Fano conv{e1 , . . . , ed , ?(e1 + Īż Īż Īż + ed )}: d ┤╬į¬ģg╠Õ d ┤╬į¬źšźĪź╬ČÓ├µ╠Õ ? d ┤╬į¬╔õė░┐šķg Pd
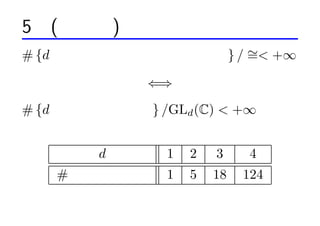
- 10. 5 (Ą═┤╬į¬) źšźĪź╬ČÓ├µ╠Õż╬ĘųŅÉ # {d ┤╬į¬ź╚®`źĻź├ź»?źšźĪź╬ČÓśö╠Õ } / Ī½< +Ī▐ = ?? # {d ┤╬į¬źšźĪź╬ČÓ├µ╠Õ } /GLd (C) < +Ī▐ d 1 2 3 4 # źšźĪź╬ČÓ├µ╠Õ 1 5 18 124
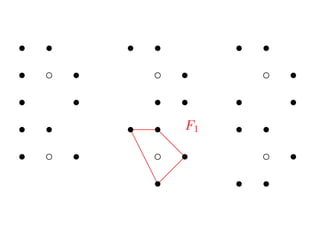
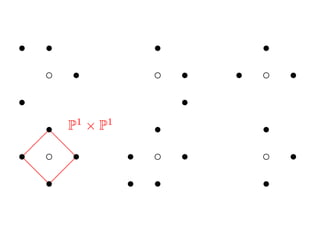
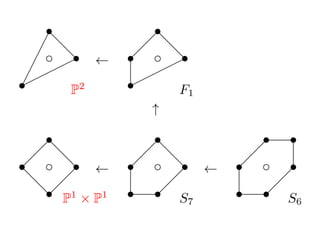
- 11. Ī½ P1 d=1 X= P = [?1, 1] ?1 s c +1 s d = 2 X Ī½ P2 , F1 , S7 , S6 , P1 Ī┴ P1 = S: ź╚®`źĻź├ź»?źŪźļź┌ź├ź─ź®Ū·├µ if ?”š : S Ī· S: ę╗ĄŃ▒¼░k (blow-up) =? S: źŪźļź┌ź├ź─ź®Ū·├µ
- 12. blow-up (ę╗░Ń) F : face {v1 , . . . , vm }: ĒöĄŃ╝»║Ž Īõ P : v := v1 + Īż Īż Īż + vm ż“ĖČż▒╝ėż©żŲąŪū┤╝ÜĘų ”š : X Īõ Ī· X: blow-up 1. X żŽę╗░Ńż╬ź╚®`źĻź├ź»żŪ┴╝żż 2. X Īõ żŽźšźĪź╬ż╚żŽŽ▐żķż╩żż Ī¦ rv2 Ī¦ r tv := v1 + v2 Ī¦ d Ī¦ F Ī¹ d P b drv1 b r PĪõ
- 13. s s ?d ?d ? c ds Ī¹ ? c ds s ?Ī¦Ī¦ Ī¦ Ī¦ Ī¦ s Ī¦ ? s Ī¦ Ī¦ P2 F1 Ī³ s s s s ?d ?d ? ? c ds Ī¹ s ? c ds Ī¹ s ? c s s d ? ? ? ds 1 ? s ? s s ? s P Ī┴ P1 S7 S6
- 14. d = 3 Batyrev (1982), Č╔▐x?Č╔▐x (1982) ĘųŅÉĘ© źįź½®`źļ╩² (=ĒöĄŃż╬╩² ? ┤╬į¬) Ī▄ 5 =? ąĪ╠’?╚²š¼ż╬Ęų└Ó▒Ēż“ź┴ź¦ź├ź» ąĪ╠’?╚²š¼ (1978) ╔õė░Ą─ź╚®`źĻź├ź»ČÓśö╠Õż╬ĘųŅÉ for d = 3 and źįź½®`źļ╩² Ī▄ 5
- 15. d = 4 Batyrev (1999), ū¶╠┘ (2000) ĘųŅÉĘ© ź╚®`źĻź├ź»╔Ł└Ēšō ĪŲn ╔Łź│®`ź¾ NE(X) = i=1 RĪ▌0 [Ci ] Ri = RĪ▌0 [Ci ]: Č╦╔õŠĆ Ci : extremal curve ”šRi : X Ī· Y : Č╦╔õģ¦┐są┤Ž± ?? Ci ż“ż─żųż╣
- 16. Ė▀┤╬į¬ż╬źšźĪź╬ČÓ├µ╠Õ (╔╚) ż“▒Ē╩Šż╣żļĘĮĘ©: Primitive relation S ? {P ż╬ĒöĄŃ }: Primitive collection ?? 1. S ūį╔ĒżŽ├µż╬ĒöĄŃ╝»║ŽżŪżŽż╩żż 2. S ż╬šµ▓┐Ęų╝»║ŽżŽżóżļ├µż╬ĒöĄŃ╝»║ŽżŪżóżļ minimal non-face
- 17. S = {x1 , . . . , xm }: primitive collection ? ?! x1 + Īż Īż Īż + xm = a1 y1 + Īż Īż Īż + an yn a1 , . . . , an > 0 {y1 , . . . , yn }: żóżļ├µż╬ĒöĄŃ╝»║Ž ? primitive relation ╚½╠Õ Ī· źšźĪź╬ČÓ├µ╠Õ (╔╚) ? extremal ray Ī· primitive relation ╔Ł└Ēšōż╚ŽÓąįż¼┴╝żż
- 18. v3 v2 s s ? v4 ? c s sv1 ? s ? s v5 v6 S6 ż╬ primitive relations: v1 + v3 = v2 , v1 + v4 = 0, v1 + v5 = v6 , v2 + v4 = v3 , v2 + v5 = 0, v2 + v6 = v1 , v3 + v5 = v4 , v3 + v6 = 0, v4 + v6 = v5
- 19. └² (V 4 : 4 ┤╬į¬ź╚®`źĻź├ź»?źšźĪź╬ČÓśö╠Õ) {e1 , e2 , e3 , e4 } ś╦£╩╗∙Ąū for Z4 P ż╬ĒöĄŃ╝»║Ž (10 ĒöĄŃ) {x0 := e1 , x1 := e2 , x2 := e3 , x3 := e4 , x4 := ?e1 , x5 := ?e2 , x6 := ?e3 , x7 := ?e4 , x8 := (e1 + e2 + e3 + e4 ), x9 := ?(e1 + e2 + e3 + e4 )} P := conv{x0 , . . . , x9 }
- 20. P ż╬ primitive relations (25 éĆ): x0 + x4 = 0, x1 + x5 = 0, x2 + x6 = 0, x3 + x7 = 0, x8 + x9 = 0, x0 + x1 + x2 = x7 + x8 , x0 + x1 + x3 = x6 + x8 , x0 + x2 + x3 = x5 + x8 , x1 + x2 + x3 = x4 + x8 , x0 + x1 + x9 = x6 + x7 , x0 + x2 + x9 = x5 + x7 , x0 + x3 + x9 = x5 + x6 , x1 + x2 + x9 = x4 + x7 , x1 + x3 + x9 = x4 + x6 , x2 + x3 + x9 = x4 + x5 , x4 + x5 + x6 = x3 + x9 , x4 + x5 + x7 = x2 + x9 , x4 + x6 + x7 = x1 + x9 , x5 + x6 + x7 = x0 + x9 , x4 + x5 + x8 = x2 + x3 , x4 + x6 + x8 = x1 + x3 ,
- 21. x4 + x7 + x8 = x1 + x2 , x5 + x6 + x8 = x0 + x3 , x5 + x7 + x8 = x0 + x2 , x6 + x7 + x8 = x0 + x1 ßß░ļ 20 éĆżŽ V 4 ż╬ extremal ray ż╦īØÅĻ NE(V 4 ) ╔Łź│®`ź¾: 20 ▒Šż╬ extremal ray ż“│ųż─ź│®`ź¾ ? R6 ?”šR : V 4 Ī· X: Č╦╔õģ¦┐są┤Ž± =? ?ipping contraction
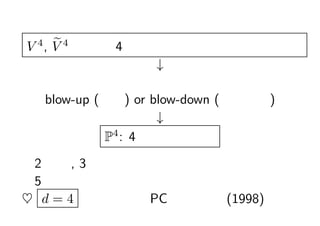
- 22. V 4 , V 4 ęį═Ōż╬ 4 ┤╬į¬ź╚®`źĻź├ź»?źšźĪź╬ČÓśö╠Õ Ī² ź╚®`źĻź├ź»?źšźĪź╬ČÓśö╠Õż╬ż▀ż“ĮUė╔ż╣żļ blow-up (▒¼░k) or blow-down (▒¼░kż╬─µ) Ī² P4 : 4 ┤╬į¬╔õė░┐šķg ?2 ┤╬į¬, 3 ┤╬į¬żŪżŌ═¼śöż╬╩ųĘ©żŪĘųŅÉ┐╔ ?5 ┤╬į¬ęį╔ŽżŪżŽ▓╗│╔┴ó ? d = 4 Ė▀ź╣ź┌ź├ź» PC żŪę╗▀Lķg (1998)
- 23. ─┐┤╬ ? Ė▀┤╬į¬ (Ī▌ 5) źšźĪź╬ČÓ├µ╠Õż╬ĘųŅÉ ? ?bro ż╬źóźļź┤źĻź║źÓ SFP ? 2 ┤╬į¬żŪ SFP īgč▌
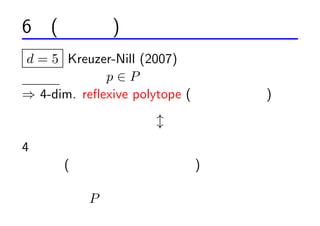
- 24. 6 (Ė▀┤╬į¬) źšźĪź╬ČÓ├µ╠Õż╬ĘųŅÉ d = 5 Kreuzer-Nill (2007) ĘųŅÉĘ© Ė„ĒöĄŃ p Ī╩ P ż╦čžż├ż┐╔õė░ż“┐╝ż©żļ ? 4-dim. re?exive polytope (Ę┤╔õĄ─ČÓ├µ╠Õ) ? 4 ┤╬į¬ź┤®`źņź¾źĘźÕź┐źżź¾?ź╚®`źĻź├ź»?źšźĪź╬ ČÓśö╠Õ (╠ž«ÉĄŃż“│ųż├ż┐ČÓśö╠Õ) ż│żņżķż½żķ P ż“╗žÅ═ż╣żļ
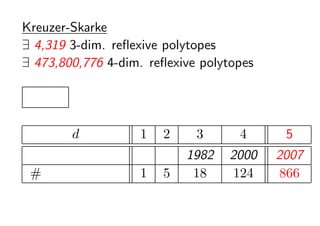
- 25. Kreuzer-Skarke ? 4,319 3-dim. re?exive polytopes ? 473,800,776 4-dim. re?exive polytopes Ęų└Ó▒Ē d 1 2 3 4 5 ─Ļ 1982 2000 2007 # źšźĪź╬ČÓ├µ╠Õ 1 5 18 124 866
- 26. 7 źóźļź┤źĻź║źÓ SFP d Ī▌ 6 ?bro (2007) ? arXiv:0704.0049 ? http://data.imf.au.dk/publications/phd /2008/imf-phd-2008-moe.pdf (Ph.D thesis, ? C++ code) SFP : Smooth Fano Polytope
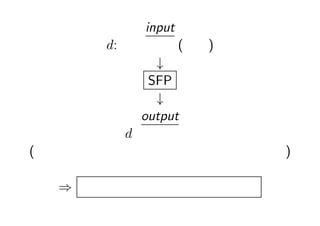
- 27. input d: š²ż╬š¹╩² (┤╬į¬) Ī² SFP Ī² output ╚½żŲż╬ d ┤╬į¬źšźĪź╬ČÓ├µ╠Õ (═¼ą═ż╩żŌż╬ż¼ųžč}żĘżŲ│÷┴”żĄżņżļż│ż╚żŽż╩żż) ? źšźĪź╬ČÓ├µ╠Õż╬ĘųŅÉ└Ēšōż╬═Ļ│╔
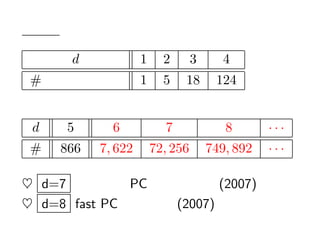
- 28. Ęų└Ó▒Ē d 1 2 3 4 # źšźĪź╬ČÓ├µ╠Õ 1 5 18 124 d 5 6 7 8 ĪżĪżĪż # 866 7, 622 72, 256 749, 892 ĪżĪżĪż ? d=7 ŲĮŠ∙Ą─ż╩ PC żŪę╗╚šęį─┌ (2007) ? d=8 fast PC żŪČ■▀Lķg (2007)
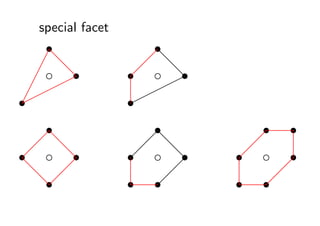
- 29. 8 special facet and embedding P : źšźĪź╬ČÓ├µ╠Õ {v1 , . . . , vm }: P ż╬ĒöĄŃ╝»║Ž F ? P : special facet ?? v1 + Īż Īż Īż + vm Ī╩ F (ż╬╔·│╔ż╣żļź│®`ź¾) {w1 , . . . , wd }: F ż╬ĒöĄŃ╝»║Ž v1 + Īż Īż Īż + vm = a1 w1 + Īż Īż Īż + ad wd (a1 , . . . , ad Ī▌ 0)
- 30. Ī∙ special facet żŽ╬©ę╗ż╚żŽŽ▐żķż╩żż s s ?d ?d ? c Ī¦s d ? c ds s Ī¦ ?Ī¦Ī¦ Ī¦Ī¦ s Ī¦ ? s Ī¦ s s s s ?d ?d ? ? c ds s ? c ds s ? c s s d ? ? ? ds ? s ? s s s ?
- 31. uF Ī╩ (Rd )? : F ż“Č©żßżļį¬ F = {?uF , ?? = 1} {uF , . . . , uF }: ╦½īØ╗∙Ąū for {w1 , . . . , wd } w1 wd Č©└Ē F : special facet =? for ?v Ī╩ P ĒöĄŃ, ?d Ī▄ ?uF , v? Ī▄ 1 and ?uF , v? = 1 ? 0 Ī▄ ?uF , v? Ī▄ 1 wi ?uF , v? = 0 ? ? 1 Ī▄ ?uF , v? Ī▄ d ? 1 wi ?uF , v? < 0 ? ?uF , v? Ī▄ ?uF , v? Ī▄ d + ?uF , v? wi for ?i
- 32. {w1 , . . . , wd } ż¼ś╦£╩╗∙Ąūż╦ż╩żļżĶż”ż╦ż╣żļ P : źšźĪź╬ČÓ├µ╠Õ =? ?Q Ī½ P s.t. = conv{e1 , . . . , ed }: special facet for Q Q: special embedding of P
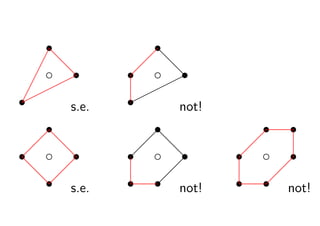
- 33. └² s s ?d ?d d ? c Ī¦s ? c ds s Ī¦ ?Ī¦Ī¦ Ī¦Ī¦ Ī¦ ? s Ī¦ s s.e. not! s s s s ?d ?d ? ? c ds s ? c ds s ? c s s d ? ? ? ds? s s ? s ? s s.e. not! not!
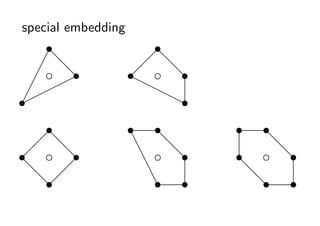
- 34. special embedding s s ?d ?d ? c ds Ī¦ ? c ds s rr ?Ī¦Ī¦ r s Ī¦ ? rs s s s s s ?d e d d ? c ds s e c ds s c ds d ? e d ds ? es s ds s
- 35. Wd ? Zd primitive lattice point ż½żķż╬ż▀ż╩żļ╝»║Ž v = (a1 , . . . , ad ) Ī╩ Wd ? ?d Ī▄ a := a1 + Īż Īż Īż + ad Ī▄ 1 and a=1? 0 Ī▄ ai Ī▄ 1 a = 0 ? ? 1 Ī▄ ai Ī▄ d ? 1 a<0? a Ī▄ ai Ī▄ d + a for ?i
- 36. Č©└ĒĪ» P : źšźĪź╬ČÓ├µ╠Õ, Q: special embedding ? {Q ż╬ĒöĄŃ╝»║Ž } ? Wd ? Wd żŽėąŽ▐╝»║Ž ? ╚½żŲż╬ d ┤╬į¬źšźĪź╬ČÓ├µ╠Õ (ż╬ special embedding) żŽ Wd ─┌ż╦╔·ŽóżĘżŲżżżļ!! ? źšźĪź╬ČÓ├µ╠Õż╬ĘųŅÉ═Ļ│╔ż╚čįż├żŲ┴╝żż
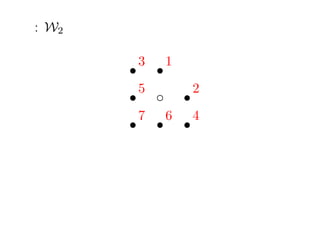
- 37. └²: W2 ? v = (a1 , a2 ) a := a1 + a2 a = 1 (0 Ī▄ ai Ī▄ 1), a = 0 (?1 Ī▄ ai Ī▄ 1), a = ?1 (?1 Ī▄ ai Ī▄ 1), a = ?2 (?2 Ī▄ ai Ī▄ 0) s s s s c s s s s #W2 = 7 s
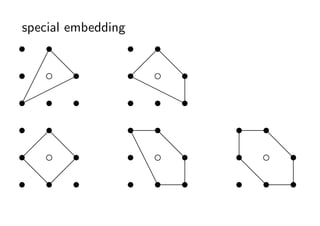
- 38. special embedding s s s s ?d ?d s ? c dsĪ¦ ? c ds s rr ?Ī¦Ī¦ r s Ī¦ s ? s s s rs s s s s s s ?d e d d ? c ds s s e c ds s c ds d ? e d s ds ? s s es s s ds s
- 39. 9 ╚½Ēśą“ for źšźĪź╬ČÓ├µ╠Õ ╚½Ēśą“ for Zd x = (x1 , . . . , xd ), y = (y1 , . . . , yd ) Ī╩ Z d x ? y ?? (?(x1 + Īż Īż Īż + xd ), x1 , . . . , xd ) Ī▄lex (?(y1 + Īż Īż Īż + yd ), y1 , . . . , yd )
- 40. └²: W2 s3 s1 s 5 c s2 s 7 s6 s4
- 41. ╚½Ēśą“ for ėąŽ▐╝»║Ž of Zd X, Y ? Z : ėąŽ▐▓┐Ęų╝»║Ž d X ? Y ?? ęįŽ┬ż╬żżż║żņż½ż¼│╔┴ó 1. X = ? 2. X, Y ?= ? and min X ? min Y 3. X, Y ?= ? and min X = min Y and X {min X} ? Y {min Y }
- 42. ╚½Ēśą“ for źšźĪź╬ČÓ├µ╠Õ P : źšźĪź╬ČÓ├µ╠Õ ord(P ) := min{Q ż╬ĒöĄŃ╝»║Ž | Q : special embedding} P1 , P2 : źšźĪź╬ČÓ├µ╠Õ P1 Ī▄ P2 ?? ord(P1 ) ? ord(P2 )
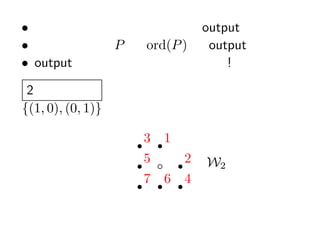
- 43. SFP 1. d Ī╩ Z>0 : input =? {e1 , . . . , ed } ż½żķź╣ź┐®`ź╚ 2. Wd ż╬▓┐Ęų╝»║Žż“ĒśĘ¼ż╦Ś╩į^ż╣żļ 3. źšźĪź╬ČÓ├µ╠Õ (ż╬ special embedding) ż╦ż╩ż├ ż┐ł÷║Ž, ēõōQ (╗∙Ąūż╬ų├ōQ) ż╦żĶż├żŲżŌż├ż╚ąĪ żĄż»ż╩żķż╩żżż½ź┴ź¦ź├ź» 4. ąĪżĄż»ż╩żķż╩żżł÷║Ž =? output ėąŽ▐╗žżŪĮK┴╦
- 44. ? ╚½żŲż╬źšźĪź╬ČÓ├µ╠Õż¼ĒśĘ¼ż╦ output żĄżņżļ ? źšźĪź╬ČÓ├µ╠Õ P ż╬ ord(P ) ż¼ output żĄżņżļ ? output żĄżņż┐źŪ®`ź┐ż“▓╬ššżĘż╩żż! 2 ┤╬į¬żŪīgč▌ {(1, 0), (0, 1)} ż½żķź╣ź┐®`ź╚ r3 r1 r5 b r2 W2 r7 r6 r4
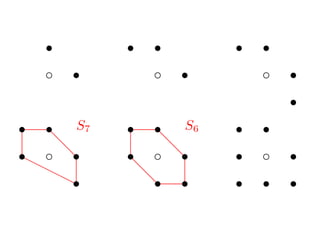
- 45. ? s s s s s c s c s c s s s s S7 s s S6 s s d d s rrc ds s c ds s c s rrs d ds s s s s
- 46. ? s s s s s s s c s c s c s s s s s s s s s s s F1 s s e d s c s e c ds c s e ? es ? s s
- 47. ? s s s s c s c s s c s s s s P1 Ī┴ P1 s s ?d ? c ds s s c s c s d ? d? s s s s
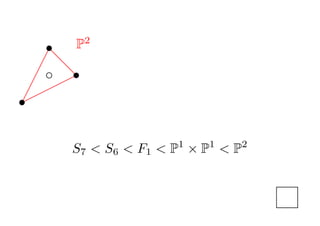
- 48. ? s P2 ?d ? c Ī¦s d ?Ī¦Ī¦ s Ī¦ ? S7 < S 6 < F 1 < P Ī┴ P < P 1 1 2 ĮK









![Ī½ P1
d=1 X= P = [?1, 1]
?1
s c +1
s
d = 2 X Ī½ P2 , F1 , S7 , S6 , P1 Ī┴ P1
=
S: ź╚®`źĻź├ź»?źŪźļź┌ź├ź─ź®Ū·├µ
if ?”š : S Ī· S: ę╗ĄŃ▒¼░k (blow-up)
=? S: źŪźļź┌ź├ź─ź®Ū·├µ](https://image.slidesharecdn.com/120919kyushu-120920204205-phpapp01/85/120919-kyushu-11-320.jpg)

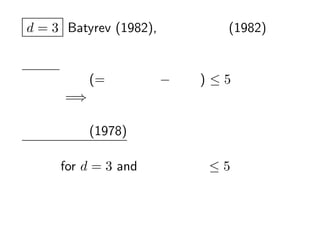
![d = 4 Batyrev (1999), ū¶╠┘ (2000)
ĘųŅÉĘ©
ź╚®`źĻź├ź»╔Ł└Ēšō
ĪŲn
╔Łź│®`ź¾ NE(X) = i=1 RĪ▌0 [Ci ]
Ri = RĪ▌0 [Ci ]: Č╦╔õŠĆ Ci : extremal curve
”šRi : X Ī· Y : Č╦╔õģ¦┐są┤Ž±
?? Ci ż“ż─żųż╣](https://image.slidesharecdn.com/120919kyushu-120920204205-phpapp01/85/120919-kyushu-15-320.jpg)