![多項式解法その1
? X の場所を固定する。
? dp[i][j]=(X からマス i に、合計戦闘回数が j 回以下で
移動するのに必要な最小移動回数)
というdpを計算する。
? BFSを用いて、それぞれのマスに対し O(RCK) で計算す
ることができる。
? a+b+c≦K (a,b,c≧0)に対して、
Xに敵がいない:dp[村][a]+2*dp[ほこら][b]+dp[城][c]
Xに敵がいる:dp[村][a]+2*dp[ほこら][b-1]+dp[城][c-1]
(b,c≧1)
で解が計算できる。](https://image.slidesharecdn.com/arc019-140320075358-phpapp01/85/AtCoder-Regular-Contest-019-20-320.jpg)
![多項式解法その2
? 発想を逆にして、
? dp1[i][j]=(村 からマス i に、合計戦闘回数が j 回以下で移
動するのに必要な最小移動回数)
? dp2[i][j]=(ほこらからマス i に、合計戦闘回数が j 回以下で
移動するのに必要な最小移動回数)
? dp3[i][j]=(城からマス i に、合計戦闘回数が j 回以下で移
動するのに必要な最小移動回数)
? とすれば、 各Xおよびa+b+c≦K (a,b,c≧0)に対して、
? 敵がいない場合:dp1[X][a]+2*dp2[X][b]+dp3[X][c]
敵がいる場合:dp1[X][a]+2*dp2[X][b-1]
+dp3[X][c-1](b,c≧1)
で最適解が計算できる。](https://image.slidesharecdn.com/arc019-140320075358-phpapp01/85/AtCoder-Regular-Contest-019-22-320.jpg)
![多項式解法その2
? すべての a,b,c に対して動かすのではなく、
? v[x]:(x=a+bとなる場合のdp1+2*dp2の最小
値)
? w[y]=(y=x+cとなる場合のv+dp3の最小値)
と 2 段階に分けて計算すれば、O(?2
)で最適
解を計算できる。
? 全体で O(???2
) となって満点が得られる。](https://image.slidesharecdn.com/arc019-140320075358-phpapp01/85/AtCoder-Regular-Contest-019-23-320.jpg)
AtCoder Regular Contest 019 解説
- 1. AtCoder Regular Contest 019? 解説
- 3. A - 問題概要 問題? 数字の一部がアルファベットに置き換わった? 文字列 S が与えられる。? 元の数を復元せよ。? ? 制限? 1 ≦ (S の文字数) ≦ 8 アルファ ベット 数字 O 0 D 0 I 1 Z 2 S 5 B 8
- 4. A - 解き方 1. 文字列 S を入力する 2. S を 1 文字目から順に見ていく 3. 各文字について、? ?数字ならばそのまま出力し? ?アルファベットならば対応する数字を出力する
- 5. A - チェックポイント 1. 文字列 S を入力する 2. S を 1 文字目から順に見ていく 3. 各文字について、? ?数字ならばそのまま出力し? ?アルファベットならば対応する数字を出力する 文字列の入出力や扱い方については 使っている言語ごとに調べよう if 文などでそのつど調べてもよし あらかじめ文字変換のハッシュテーブルを用意するもよし
- 6. B問題 こだわりの名前
- 7. B - 問題概要 問題? 英大文字からなる名前 A が与えられる。? これを 1 文字だけ別のアルファベットに変換して? 作れる回文でない文字列は何個あるか？? ? 制限? 1 ≦ (A の文字数) ≦ 3×105
- 8. B - 考えよう まずはじめに? 書かれていることをそのまま計算することはできる? ?→1文字の変更を全部試して、回文かどうか判定する 計算量は？? ?変更候補が 25 × N ≦ 7,500,000 通り? ?回文かを試すのに O(N) 時間? ?→ 25 × N × N ≦ 2,250,000,000,000 ≒ 2 × 1012? ??はとうてい 2 秒では無理……
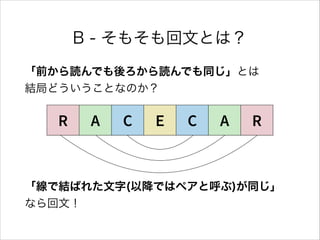
- 9. B - そもそも回文とは？ 「前から読んでも後ろから読んでも同じ」とは? 結局どういうことなのか？ R A C E C A R 「線で結ばれた文字(以降ではペアと呼ぶ)が同じ」? なら回文！
- 11. B - 解き方(2/2) 重要な考察? 1 文字の変更では「文字が一致するペアの数」は? 1 増えるか、1 減るか、そのままか? のいずれかである。? ?(1 文字しか変えてないのだから、当たり前) これにより、1 文字変更した後の回文の判定が ? O(1) の計算量でできるようになる！? ?→これなら時間制限にも間に合う
- 12. C 問題 最後の森 解説担当:城下 慎也 (@phidnight)
- 13. はじめに ? この問題において入力に不備が見つかった ため、ノーコンテストとなってしまい、誠に申し 訳ありませんでした。 ? このようなことが再び起こらないように今後も 気をつけていきたいと思います。
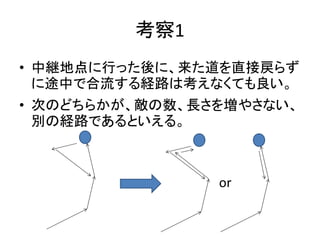
- 14. 概要 ? R*C のマス目が与えられる。 ? 村→ほこら→城 の経路で長さ最小なものを考 えたい。 ? 途中にいる敵は K 体まで倒すことができる。 ? 一度倒した敵は復活しない。
- 15. 倒す敵が決まると? ? 最短経路問題を 2 回解くことで解が得られる ようになる。 ? ただ、敵の総数を E としたとき、 ? ?? だけ組み 合わせを試さなければならないので指数オー ダー。 ? DP を使おうにも、倒した敵が復活しないとこ ろを情報としてうまく保存するのが難しい。 ? まずは多項式解法を求めよう！
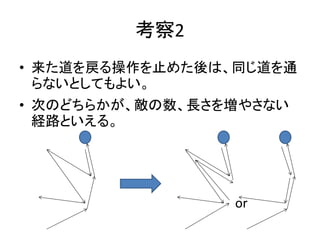
- 16. 指数を回避するために ? 倒した敵を情報として持たないようにしたい。 ? すべての経路ではなく、最適性を維持したま ま、うまく状態を持てるような経路だけを考え たい。 ? 必要な経路を厳选しよう！
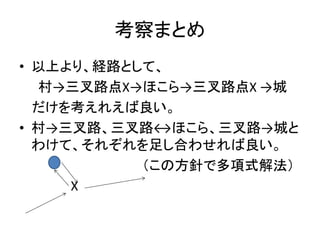
- 19. 考察まとめ ? 以上より、経路として、 村→三叉路点X→ほこら→三叉路点X →城 だけを考えれえば良い。 ? 村→三叉路、三叉路?ほこら、三叉路→城と わけて、それぞれを足し合わせれば良い。 （この方針で多項式解法） X
- 20. 多項式解法その1 ? X の場所を固定する。 ? dp[i][j]=(X からマス i に、合計戦闘回数が j 回以下で 移動するのに必要な最小移動回数) というdpを計算する。 ? BFSを用いて、それぞれのマスに対し O(RCK) で計算す ることができる。 ? a+b+c≦K (a,b,c≧0)に対して、 Xに敵がいない:dp[村][a]+2*dp[ほこら][b]+dp[城][c] Xに敵がいる:dp[村][a]+2*dp[ほこら][b-1]+dp[城][c-1] (b,c≧1) で解が計算できる。
- 21. 多項式解法その1 ? dpの計算に O(RCK) かかり、 ? すべての a,b,c の組を試すのに O(?3 )かかる ので、各 X に対し全体で O(RCK+?3 ) ? 全体でO(?2 ?2 ? + ???3 ) ? この解法だとTLEしてしまう。
- 22. 多項式解法その2 ? 発想を逆にして、 ? dp1[i][j]=(村 からマス i に、合計戦闘回数が j 回以下で移 動するのに必要な最小移動回数) ? dp2[i][j]=(ほこらからマス i に、合計戦闘回数が j 回以下で 移動するのに必要な最小移動回数) ? dp3[i][j]=(城からマス i に、合計戦闘回数が j 回以下で移 動するのに必要な最小移動回数) ? とすれば、 各Xおよびa+b+c≦K (a,b,c≧0)に対して、 ? 敵がいない場合:dp1[X][a]+2*dp2[X][b]+dp3[X][c] 敵がいる場合:dp1[X][a]+2*dp2[X][b-1] +dp3[X][c-1](b,c≧1) で最適解が計算できる。
- 23. 多項式解法その2 ? すべての a,b,c に対して動かすのではなく、 ? v[x]:(x=a+bとなる場合のdp1+2*dp2の最小 値) ? w[y]=(y=x+cとなる場合のv+dp3の最小値) と 2 段階に分けて計算すれば、O(?2 )で最適 解を計算できる。 ? 全体で O(???2 ) となって満点が得られる。
- 24. D 問題 ほんとうのたたかい 解説担当:城下 慎也 (@phidnight)
- 25. 概要 ? N*N のフィールドの上にいくつか O を置く。 ? 4 つの隅が軸に平行な長方形とならないよう に配置する。 ? できるだけ多く O を配置したい。 ? 2≦N≦150
- 26. 部分点1 ? 5 点解法 (“．”を”X”に置き換えています) OOO…O OXX…X OXX…X ： ： OXX…X
- 27. 部分点2 ? 10 点解法 (“．”を”X”に置き換えています) XOO…O OOX…X OXO…X ： ： OXX…O
- 28. 部分点3 ? それ以上を得たい場合 ? ランダムに置くと強い ? うまく貪欲にすると強い ? 焼きなますと強い ? etc… ? 満点を得たい場合は?
- 29. 考察 ? そもそも理論的にはどれくらい置けるだろう? ? 長方形が成立する条件を考えると、 ? 長方形が成立する? (i,j), (i,l), (k,j), (k,l) のい ずれにも O があるような i<k , j<l が存在する ? 各行 p ごとに、(p,q) と (p,r) (q<r) のいずれに も O があるなら、(q,r) というペアを保存する、 という処理を行うと、上記の条件が成立する 場合に、i 行目と k 行目でペア (j,l) が保存さ れることになる。
- 30. 考察 ? このように考えると、実は 長方形が成立する?同じペアが複数出てくる ? という式が成立することになる。 ? 裏を返すと、同じペアは高々 1 回しか出ないこと になる。 ? ペアの総数は N(N-1)/2 個であり、ある行に m 個 あればペアの数が m(m-1)/2 だけ減るので、 ? N(N-1)/2 ≦ ??(?? ? 1)/2? ?=1 が成立する。ただし??は ? 行目の O の総数。
- 31. 考察 ? 右辺の式は??のばらつきが少ないほど ?? ? ?=1 が一定の場合に小さくなる。 ? 置ける O の最大数はおよそ? ? 個となる。 ? このこと (できるだけまばらに置く) を踏まえる と良い解が得られる。
- 32. N=p*p (p:素数) のとき ? このときに p*p*p 個の O を置く配置を発見す る。 ※素数のほうが作りやすいので、素数にしてい ます。 ? 例: 第 p*(i-1)+j (1≦i,j≦p) 行目の、 p*(k-1)+1 から p*k 列(1≦k≦p)までの範囲には、 i*k+j を p で割った余りを q としたとき、 (p*(i-1)+j, p*(k-1)+1+q) にのみ O を置く。
- 34. 100点解法例 ? さっきの p を p=11 とすれば S=1331 が得られ る。 ? しかしながら 150 に対しては未使用な部分が 存在する。 ? そこで p=13 として、左上の 150*150 の領域 を取り出すことにすれば良い。 ? 結果、S=1700超となり、100点が得られる。