![変分推定のレシピ
1. モデルを考える ?(?, ?)
2. 潜在変数の近似分布を選ぶ ?(?; ?)
3. ELBOを定式化
? ? = E ?(?;?)[log ? ?, ? ? log? ?: ? ]
4. 期待値（積分）を計算
? ? = ??2
+ log ?: Example
5. 導関数を求める
??? ? = 2?? +
1
?
6. 最適化する
? ?+1 = ? ? + ?? ??? ?](https://image.slidesharecdn.com/nipsvariationalinference-foundationsandmodernmethods-170320152930/85/nips-variational-inference-foundations-and-modern-methods-36-320.jpg)
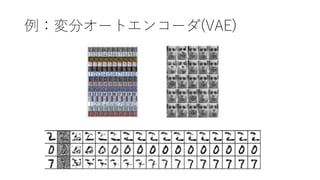
第３回nips読み会?関西『variational inference foundations and modern methods』
- 1. Variational Inference: Foundations and Modern Methods 担当：落合幸治@理化学研究所 第３回nips読み会?関西 2017/3/18(土) David Blei @Columbia University Shakir Mohamed @DeepMind Rajesh Ranganath @Princeton University NIPS 2016 Tutorial · December 5, 2016
- 2. 注意 ? もしこのスライドを見てわからない点があったら（翻訳ミスの可能 性があるため）以下元資料を確認 ? まとめ https://nips.cc/Conferences/2016/Schedule?showEvent=6199 ? Video https://channel9.msdn.com/Events/Neural-Information- Processing-Systems-Conference/Neural-Information-Processing- Systems-Conference-NIPS-2016/Variational-Inference- Foundations-and-Modern-Methods ? 狠狠撸(PDF) https://media.nips.cc/Conferences/2016/狠狠撸s/6199-狠狠撸s.pdf
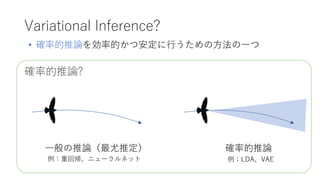
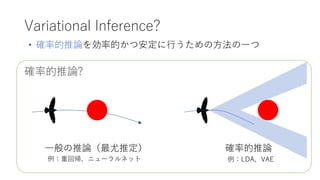
- 3. Variational Inference? 一般の推論（最尤推定） 確率的推論? ? 確率的推論を効率的かつ安定に行うための方法の一つ 確率的推論 例：重回帰、ニューラルネット 例：尝顿础、痴础贰
- 4. 確率的推論? Variational Inference? 一般の推論（最尤推定） ? 確率的推論を効率的かつ安定に行うための方法の一つ 確率的推論 例：重回帰、ニューラルネット 例：尝顿础、痴础贰
- 5. 確率的推論 ? 推論先の点がつねに一点にさ だまるとは限らない ? 例：画像の上半分から 下半分を推測→ ? 分布の期待値がつねにもっと も良い結果とは限らない ? 自然画像の期待値（平均値）は のっぺりした灰色の画像
- 6. 質問 1. 確率的勾配法(stochastic gradient descent, SGD)とは 何か知っている or 使ったことがある 2. 『パターン認識と機械学習』の9章：混合モデルとEM、 １０章：変分推論を読んだことがある 3. Variational Autoencoderという言葉を聞いたことがあ る
- 7. 目次 1. 変分推論とは 2. 平均場近似と確率的変分推論 3. 変分下界に対する確率的勾配法 4. 平均場近似を仮定しない変分推論 ※オリジナルのチュートリアルに準拠
- 8. 目次 1. 変分推論とは 2. 平均場近似と確率的変分推論 3. 変分下界に対する確率的勾配法 4. 平均場近似を仮定しない変分推論 ※オリジナルのチュートリアルに準拠 ? SGDを知っていればここまでは簡単
- 9. 目次 1. 変分推論とは 2. 平均場近似と確率的変分推論 3. 変分下界に対する確率的勾配法 4. 平均場近似を仮定しない変分推論 ※オリジナルのチュートリアルに準拠 ? 一番の難所 ? PRMLの9章、10章の内容を発展 ? VAEの理論的背景がわかる
- 10. 目次 1. 変分推論とは 2. 平均場近似と確率的変分推論 3. 変分下界に対する確率的勾配法 4. 平均場近似を仮定しない変分推論 ※オリジナルのチュートリアルに準拠 ? 現代の（2016年以降の）研究 ? 事前知識があると少し感動する
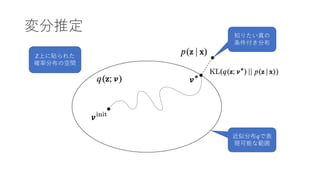
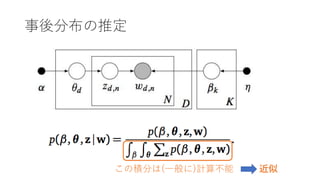
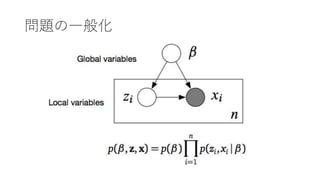
- 12. 確率的推論 ? 確率モデルとは観測変数?と隠れ変数?の同時分布 ?(?, ?) ? 確率モデルがあれば未知変数も事後分布として求められる ? ? ? = ?(?, ?) ? ?, ? ?? ? 例えばxを画像zをラベルとすると分類問題がとける ? ほとんどの問題において分母の積分が解けないので近似が必要
- 14. 歴史 ? 変分推定は統計力学のアイディアを確率推定に適用することで 始まりました。おそらく80年代にPetersonとAndersonが平均 場法をニューラルネットで使ったことが始まりです。 ? このアイディアはJordan研究室で1990年代に取り上げられ、 Tommi Jaakkola, Lawrence Saul, Zoubin Gharamani によって 多くの確率モデルに一般化されました。 ? それと並行してHintonとVan Campがニューラルネットによる 平均場法を開発(1993)。NealとHintonはこのアイディアをEM 法につなげそれがmixture of expertsやHMMなどへ変分法をさ らに進展させました。
- 15. 現在 ? 現在では変分法における多くの活発な取り組みがあります。大 規模化、簡易化、高速化、正確化、複雑なモデルへの適用と応 用 ? 現在の変分推定は多くの領域にまたがっています：確率的プロ グラミング、強化学習、ニューラルネット、凸最適化、ベイズ 統計、そして広範囲にわたる応用分野。 ? このスライドの目的は基礎から始まり、いくつかの最近のアイ ディアを紹介し、新研究における最前線を知ってもらうことで す。
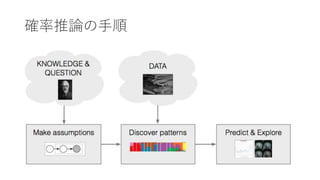
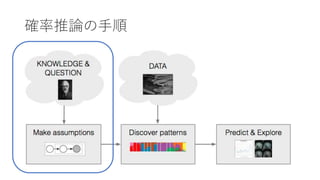
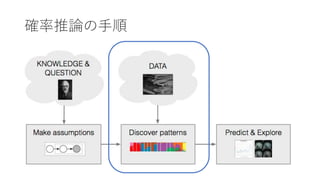
- 17. 确率推论の手顺
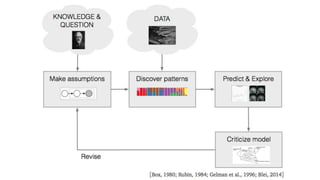
- 20. 确率推论の手顺
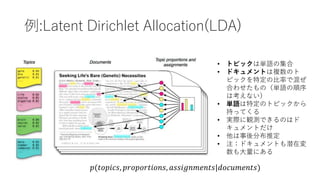
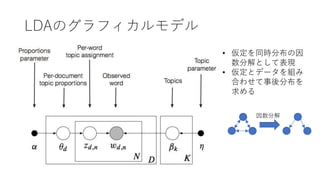
- 21. 例:Latent Dirichlet Allocation(LDA) ? トピックは単語の集合 ? ドキュメントは複数のト ピックを特定の比率で混ぜ 合わせたもの（単語の順序 は考えない） ? 単語は特定のトピックから 持ってくる ? 実際に観測できるのはド キュメントだけ ? 他は事後分布推定 ? 注：ドキュメントも潜在変 数も大量にある ?(??????, ???????????, ???????????|?????????)
- 23. 确率推论の手顺
- 26. Evidence Lower Bound(ELBO) ? log ? ? の下界 ? ELBO最大化はKLダイバージェンスの最小化にな （なぜそうなるかは3章で説明） ? 最初の項はMAP推定に相当 ? 第二項(エントロピー)は?を可能な限り拡散させる エントロピー
- 27. 问题の一般化
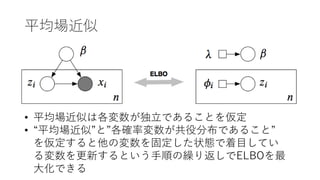
- 29. 古典的変分推定
- 30. 確率的変分推定 ? 大規模データに 対応 ? 確率的勾配法と 同じ発想 ? ステップサイズ 系列ρ ?は Robbins-Monro conditionsに従う ものとする（大 まかには徐々に 小さくなってい くと思っておけ ば良い）
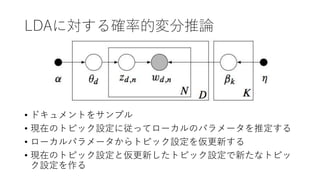
- 31. LDAに対する確率的変分推論 ? ドキュメントをサンプル ? 現在のトピック設定に従ってローカルのパラメータを推定する ? ローカルパラメータからトピック設定を仮更新する ? 現在のトピック設定と仮更新したトピック設定で新たなトピッ ク設定を作る
- 32. 自動抽出さ れたトピッ クと単語
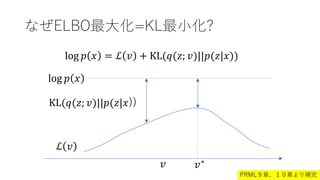
- 34. なぜELBO最大化=KL最小化? log ? ? = ? ? + KL(?(?; ?)||?(?|?)) log ? ? ? ? KL(?(?; ?)||?(?|?)) ? ?? PRML９章、１０章より補完
- 36. 変分推定のレシピ 1. モデルを考える ?(?, ?) 2. 潜在変数の近似分布を選ぶ ?(?; ?) 3. ELBOを定式化 ? ? = E ?(?;?)[log ? ?, ? ? log? ?: ? ] 4. 期待値（積分）を計算 ? ? = ??2 + log ?: Example 5. 導関数を求める ??? ? = 2?? + 1 ? 6. 最適化する ? ?+1 = ? ? + ?? ??? ?
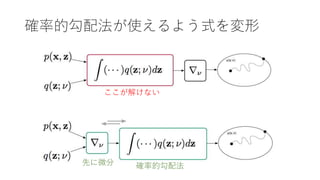
- 37. 現実は甘くない ? ベイズロジスティック回帰を変分推定しようとした結果（xが入力y が出力zが回帰係数） ? 期待値が解析的に求められない + 変分係数に関係する値(z)が期待 値の中に残っている = 導関数が求められない
- 39. 式変形 ELBO Define
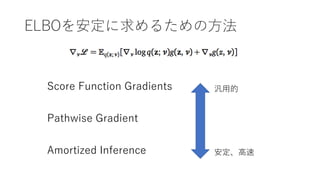
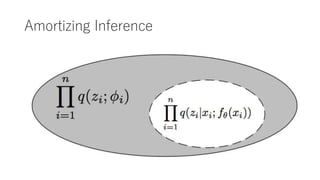
- 40. ELBOを安定に求めるための方法 Score Function Gradients Pathwise Gradient Amortized Inference 汎用的 安定、高速
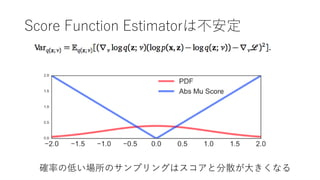
- 41. Score Function Estimator 単純化 再掲 勾配 Likelihood ratio(尤度)またはREINFORCE gradients(強化学習勾配?) ともよばれる
- 42. 単純化について補足 nips読み会での議論を踏まえ追加 ? ? ??g ?, ? = ? ? ??log? ?; ? g ?, ? = log? ?, ? ? log ?(?; ?) = ?(?; ?)??log? ?; ? ?? = ?(?; ?) ?? ? ?; ? ?(?; ?) ?? = ?? ? ?; ? ?? = ?? ? ?; ? ?? = 0 =1 微分と積分の順序交換より
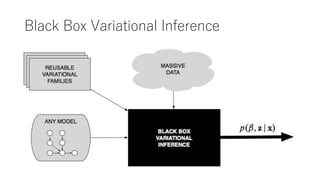
- 44. Black Box Variational Inference 適用のための条件 ? ?(?)からサンプリング可能 ? ?? log ?(?; ?)が計算可能 ? log ?(?, ?)とlog ?(?)が計算可能 モデル固有の作業がない：汎用的な適用が可能
- 45. Black Box Variational Inference
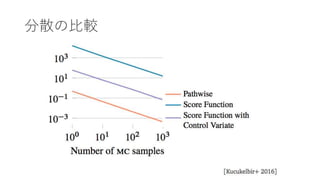
- 50. 分散の比较
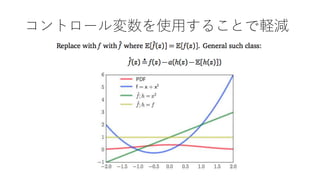
- 56. 全般的なアドバイス ? もし?(?, ?)が?について微分可能だったら ? リパラメタライゼーションが可能な?を使いなさい ? もし?(?, ?)が?について微分不可能だったら ? コントロール変数ありのScore Functionを使いなさい ? 実験的証拠に基づいてさらに分散を減少させなさい （意訳：試行錯誤で頑張って分散を下げなさい） ? 全般的に ? 座標ごとにラーニングレートを調節(RMSProp, AdaGrad) ? アニーリング + 温度 ? サンプリングを並列化できないか一度考えてみる
- 57. Software
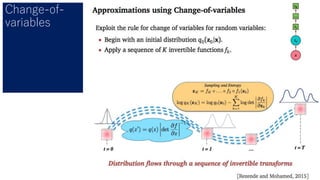
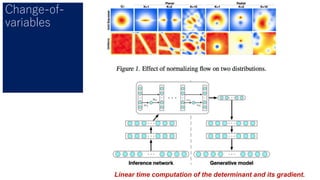
- 64. Change-of- variables Linear time computation of the determinant and its gradient.
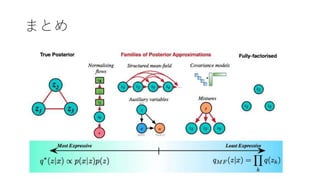
- 68. まとめ
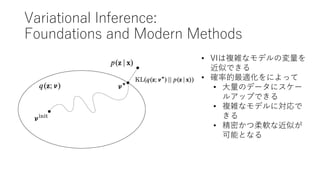
- 69. Variational Inference: Foundations and Modern Methods ? VIは複雑なモデルの変量を 近似できる ? 確率的最適化をによって ? 大量のデータにスケー ルアップできる ? 複雑なモデルに対応で きる ? 精密かつ柔軟な近似が 可能となる