狠狠撸

よいモデルを選びたい
“The Oracle Properties of Feature Selection using Lassos”
１．「罰則付き回帰とデータ解析環境R」の一部をRでトレースします
(荒木孝治，オペレーションズ?リサーチ2013 年 5 月号，261-266)
２．{hdm} packageを紹介します
(DJ Stekhoven, P Bühlmann (2011), Bioinformatics 28 (1), 112-118)
第５４回R勉強会＠東京（#TokyoR）
Lassoにおける変数選択とオラクル性
十分なサンプルサイズなデータに対する手法の比較
超高次元（p>>n）なデータに対する手法の比較

変数選択(モデル選択) どうしてますか?
オペレーションズ?リサーチ2013 年 5 月号，261-266

Lasso
? 線形重回帰モデルで、最小二乗法で係数を推定をする際に、
推定量(β)の絶対値を大きくしたくない
? 未定乗数法で書くと：
|β|の大きさに対する罰則項最小二乗法
λは罰則の大きさを
調整するパラメータ
βの絶対値を大きさを
定数ｔ以下に抑えたい
最小二乗法

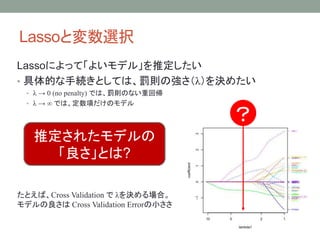
Lassoと変数選択
Lassoによって「よいモデル」を推定したい
? 具体的な手続きとしては、罰則の強さ（λ）を決めたい
? λ → 0 (no penalty) では、罰則のない重回帰
? λ → ∞ では、定数項だけのモデル
推定されたモデルの
「良さ」とは?
たとえば、Cross Validation で λを決める場合。
モデルの良さは Cross Validation Errorの小ささ
？

Lassoの変数選択とオラクル性（Oracle Property）
真のモデルをなるべく精度良く再現したい
? 選択される変数の一致性（selection consistency）
? 重要な変数を取りこぼさず選択し、ノイズとなる変数はすべて除外する
? サンプルサイズn が大きくなるとき，0 でない係数（βj = 0）を持つ説明変数が正しく選択される確率
が1 に収束する
? 推定量の一致性（estimation consistency）
? 非ゼロな係数の推定量は、真値に収束する
? 0 でない係数を持つ説明変数に対する推定量が、漸近不偏，漸近正規性を持つ
J. Fan and R. Li, Variable selection via nonconcave penalized likelihood and its oracle properties.
Jour-nal of the American Statistical Association, 96 , 1348–1360, 2001.

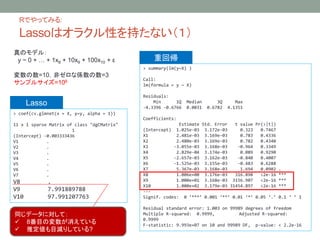
Rでやってみる:
Lassoはオラクル性を持たない（１）
> summary(lm(y~X) )
Call:
lm(formula = y ~ X)
Residuals:
Min 1Q Median 3Q Max
-4.3396 -0.6766 0.0031 0.6782 4.1351
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.025e-03 3.172e-03 0.323 0.7467
X1 2.481e-03 3.169e-03 0.783 0.4336
X2 2.480e-03 3.169e-03 0.782 0.4340
X3 -3.055e-03 3.168e-03 -0.964 0.3349
X4 2.829e-04 3.174e-03 0.089 0.9290
X5 -2.657e-03 3.162e-03 -0.840 0.4007
X6 -1.525e-03 3.155e-03 -0.483 0.6288
X7 5.367e-03 3.168e-03 1.694 0.0902 .
X8 1.006e+00 3.176e-03 316.898 <2e-16 ***
X9 1.000e+01 3.168e-03 3156.907 <2e-16 ***
X10 1.000e+02 3.179e-03 31454.897 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.003 on 99989 degrees of freedom
Multiple R-squared: 0.9999, Adjusted R-squared:
0.9999
F-statistic: 9.993e+07 on 10 and 99989 DF, p-value: < 2.2e-16
> coef(cv.glmnet(x = X, y=y, alpha = 1))
11 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) -0.003333436
V1 .
V2 .
V3 .
V4 .
V5 .
V6 .
V7 .
V8 .
V9 7.991889788
V10 97.991207763
同じデータに対して：
? 8番目の変数が消えている
? 推定値も目減りしている?
真のモデル：
y ~ 0 + … + 1x8 + 10x9 + 100x10 + ε
変数の数=10，非ゼロな係数の数=3
サンプルサイズ=106
重回帰
Lasso

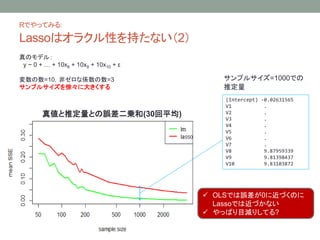
Rでやってみる:
Lassoはオラクル性を持たない（2）
(Intercept) -0.02631565
V1 .
V2 .
V3 .
V4 .
V5 .
V6 .
V7 .
V8 9.87959339
V9 9.81398437
V10 9.83103872
サンプルサイズ=1000での
推定量
真値と推定量との誤差二乗和(30回平均)
? OLSでは誤差が0に近づくのに
Lassoでは近づかない
? やっぱり目減りしてる?
真のモデル：
y ~ 0 + … + 10x8 + 10x9 + 10x10 + ε
サンプルサイズを徐々に大きくする

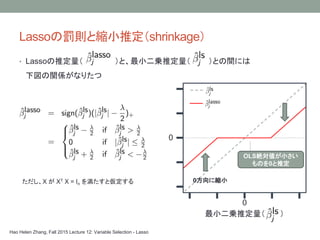
Lassoの罰則と縮小推定（shrinkage）
ただし、X が XT X = In を満たすと仮定する
0
0
0方向に縮小
OLS絶対値が小さい
ものを0と推定
最小二乗推定量（）
Hao Helen Zhang, Fall 2015 Lecture 12: Variable Selection - Lasso
? Lassoの推定量（）と、最小二乗推定量（）との間には
下図の関係がなりたつ

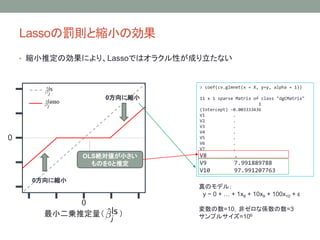
Lassoの罰則と縮小の効果
? 縮小推定の効果により、Lassoではオラクル性が成り立たない
0
0
0方向に縮小
0方向に縮小
OLS絶対値が小さい
ものを0と推定
最小二乗推定量（）
> coef(cv.glmnet(x = X, y=y, alpha = 1))
11 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) -0.003333436
V1 .
V2 .
V3 .
V4 .
V5 .
V6 .
V7 .
V8 .
V9 7.991889788
V10 97.991207763
真のモデル：
y ~ 0 + … + 1x8 + 10x9 + 100x10 + ε
サンプルサイズ=106

オラクル性保証付きLasso
H. Zou: The adaptive lasso and its oracle properties, Journal of the American Statistical Association, 101, 1418–1429, 2006.
Hao Helen Zhang, Fall 2015, Lecture 13: Variable Selection - Beyond LASSO
データ依存的に最適な重みが選ばれる
Adaptive Lassoのほかにも色々と提案されているが割愛
Adaptive Lasso
? 推定の偏りを減少させる重みづけ
? 0 に近い推定量に対しては大きな重みを適用して 0 にする
? 絶対値の大きな推定量に対しては，小さな重みを適用することで縮小の効果を減らす
? 2段階の推定手順
? β の初期推定量を求める
? １を利用した重みを利用する?１罰則付き回帰を行う

Rでやってみる：
オラクル性保証付きLassoを使うことで改善
? 罰則項を工夫することで、Lassoにオラクル性を持たせる
? 今回はmsgpsパッケージのadaptive Lassoを使う
? 選択基準はBICを使う
fit.alasso <- msgps(X= X, y=c(y), penalty="alasso",gamma=1, lambda=0)
coeff.alasso <- coef(fit.alasso) %>>% data.frame %>>% select(BIC) %>>% unlist
sse.alasso <- (this_data$beta - coeff.alasso[-1])^2 %>>% sum
真値と推定量との誤差二乗和(30回平均)
? オリジナルと比べて良い精度
真のモデル：
y ~ 0 + … + 10x8 + 10x9 + 10x10 + ε
? 変数の数=10
? 非ゼロな係数の数=3
? サンプルサイズを徐々に大きくする
推定精度=真値と推定量との誤差二乗和

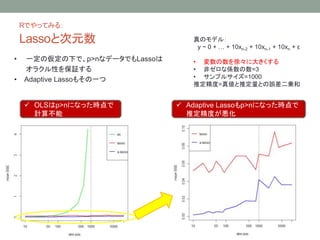
Lassoと次元数
? 従来の回帰分析の数学的妥当性は、p<n条件下で保証されていた
? 高次元データ(p>n)の場合、それが破綻する。いわゆる「次元の呪い」
? Lassoではスパース性を仮定する
? 「候補変数のなかで真に効果を持つ変数の数(d)は非常に少数である」という仮定
? p>n>>d
? 一定の仮定の下で、p>nなデータでもオラクル性を保証する
? Adaptive Lassoもその一つ
? Huang, J. et al.: Adaptive lasso for sparse high dimensional regression, Stat. Sin., 18: 1603-1618, 2007.
ゲノムワイド関連解析の統計学的問題点とその解決
植木優夫, 田宮元, 医学のあゆみ第230巻12号(2009年9月19日号) (1079-1080)

Rでやってみる：
Lassoと次元数
? 一定の仮定の下で、p>nなデータでもLassoは
オラクル性を保証する
? Adaptive Lassoもその一つ
? OLSはp>nになった時点で
計算不能
? Adaptive Lassoもp>nになった時点で
推定精度が悪化
真のモデル：
y ~ 0 + … + 10xn-2 + 10xn-1 + 10xn + ε
? 変数の数を徐々に大きくする
? サンプルサイズ=1000

Lassoと次元数
? 高次元データ(p>>n)の場合
1. 何らかの手順でいったん次元圧縮を行う
2. 圧縮したデータで、あらためて係数を高精度に推定する
? 手法の例
? p>>nでも、一定の仮定の下で選択の一致性が保証されている
? Adaptive Lasso
? Huang, J. et al.: Adaptive lasso for sparse high dimensional regression, Stat. Sin., 18: 1603-1618, 2007.
? L2 boosting
? Buhlmann, P.: Boosting for high-dimensional linear models. Ann. Statist., 34:559-583, 2006.
? 変数のランキングに基づくスクリーニング
? SURE independence screening (SIS)
? Fan, J. and Lv, J.: Sure independence screening for ultrahigh dimensional feature space (with
discussion). J. R. Statist. Soc B, 70: 849-911, 2008.
? Lassoで頑張る
? 誤って非ゼロとした係数はすべてゼロに近い値で収まる性質を使う
? Meinshausen, N. and Yu, B.: Lasso-type recovery of sparse representations of high-dimensional data. To
appear in Ann. Statist.
ゲノムワイド関連解析の統計学的問題点とその解決
植木優夫, 田宮元, 医学のあゆみ第230巻12号(2009年9月19日号) (1079-1080)

“rigorous” lasso in hdm package
rlassoの特色
? Post-Lassoによる、変数事前のスクリーニング
? Lassoで係数の推定量が0にされた変数を除去してから、最小二乗法をおこなう
? 罰則強度(λ)を理論的背景のもとで与える
? 誤差の等分散性の仮定の有無 × data-driven or Not で、合計４パターンの罰則項を提案
? 推定した係数の信頼区間を提供する
? Shooting Lasso Algorithmによる高速化
V Chernozhukov, C Hansen, M Spindler (2016+). hdm: High-Dimensional Metrics R Journal, forthcoming
https://cran.rstudio.com/web/packages/hdm/
高次元データ(p>>n)の場合
1. 何らかの手順でいったん次元圧縮を行う
2. 圧縮したデータのもとで、あらためて係数を高精度に推定する

hdm::rlassoを使ってみる
rlasso(
formula, data,
post = TRUE, # TRUEでPost-Lasso。 FALSEで独自の罰則だけrigorousなLasso
intercept = TRUE, # TRUEで切片項(β0）の罰則付き推定をしない
penalty = list(homoscedastic = FALSE, # FALSEで誤差の等分散性を仮定しない
X.dependent.lambda = FALSE, # TRUEでデータ依存的なλの選択をする
lambda.start = NULL,
c = 1.1,
gamma = 0.1/log(n)),
control = list(numIter =15,
tol = 10^-5,
threshold = NULL),
...)

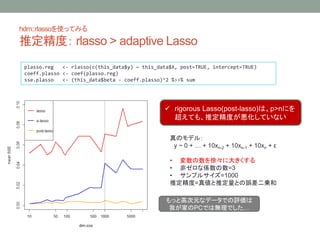
推定精度： rlasso > adaptive Lasso
plasso.reg <- rlasso(c(this_data$y) ~ this_data$X, post=TRUE, intercept=TRUE)
coeff.plasso <- coef(plasso.reg)
sse.plasso <- (this_data$beta - coeff.plasso)^2 %>>% sum
? rigorous Lasso(post-lasso)は、p>nにを
超えても、推定精度が悪化していない
もっと高次元なデータでの評価は
我が家のPCでは無理でした…
真のモデル：
y ~ 0 + … + 10xn-2 + 10xn-1 + 10xn + ε
? 変数の数を徐々に大きくする
? サンプルサイズ=1000

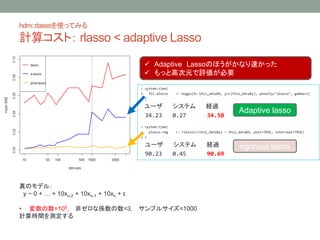
計算コスト： rlasso < adaptive Lasso
> system.time(
+ fit.alasso <- msgps(X= this_data$X, y=c(this_data$y), penalty="alasso", gamma=1)
+ )
ユーザシステム経過
34.23 0.27 34.50
> system.time(
+ plasso.reg <- rlasso(c(this_data$y) ~ this_data$X, post=TRUE, intercept=TRUE)
+ )
ユーザシステム経過
90.23 0.45 90.69
Adaptive lasso
rigorous lasso
? Adaptive Lassoのほうがかなり速かった
? もっと高次元で評価が必要
真のモデル：
y ~ 0 + … + 10xn-2 + 10xn-1 + 10xn + ε
? 変数の数=105，非ゼロな係数の数=3，サンプルサイズ=1000
計算時間を測定する

まとめ
オペレーションズ?リサーチ2013 年 5 月号，261-266
“rigorous” lasso
V Chernozhukov, C Hansen, M Spindler (2016+). hdm: High-Dimensional Metrics
R Journal, forthcoming
https://cran.rstudio.com/web/packages/hdm/

狠狠撸

Oracle property and_hdm_pkg_rigorouslasso

More Related Content

What's hot (20)

Similar to Oracle property and_hdm_pkg_rigorouslasso (20)

More from Satoshi Kato (13)

Oracle property and_hdm_pkg_rigorouslasso