Arc041
- 1. ARC #041 ĮŌšh ĮŌšhź╣źķźżź╔ĄŻĄ▒ : @sugim48
- 2. å¢Ņ} A ©C ź│źżź¾ż╬Ę┤▄×
- 3. å¢Ņ}Ė┼ę¬ ? ▒ĒŽ“żŁż╬ź│źżź¾ż¼ ? ├ČĪóčYŽ“żŁż╬ź│źżź¾ż¼ ? ├ČżóżļĪŻż┴żńż”ż╔ ? ├Čż╬ ź│źżź¾ż“▀xżėĪóżĮżņżķż╣ż┘żŲż“żęż├ż»żĻĘĄż╣ĪŻżĮż╬ĮY╣¹Īó▒ĒŽ“żŁż╬ź│źż ź¾żŽūŅ┤¾żŪ║╬├Čż╦ż╩żļż½Ż┐ ? 1 Ī▄ ?, ? Ī▄ 106Ż¼1 Ī▄ ? Ī▄ ? + ?
- 4. ĮŌĘ© 1 ? żęż├ż»żĻĘĄżĘż┐ĮY╣¹Īó▒ĒŽ“żŁż╬ź│źżź¾ż“żŪżŁżļż└ż▒ČÓż»żĘż┐żżĪŻ ? ż▐ż║żŽčYŽ“żŁż╬ź│źżź¾ż½żķżęż├ż»żĻĘĄżĘżŲżżżŁĪó? ż╦£║ż┐ż╩ż▒żņżą▒Ē Ž“żŁż╬ź│źżź¾żŌżęż├ż»żĻĘĄżĘżŲżżż»ĪŻ ? ż┴żńż”ż╔ ? = ? ż╩żķżąĪóż╣ż┘żŲż╬ź│źżź¾ż“▒ĒŽ“żŁż╦żŪżŁżļĪŻ? Ī┘ ? ż╩żķ żąĪóź║źņż╬Ęųż└ż▒čYŽ“żŁż╬ź│źżź¾ż¼▓ążļĪŻ ? ┤ż©żŽ ? + ? ? |? ? ?|
- 5. ĮŌĘ© 2 ? Į±╗žżŽ ?, ? Ī▄ 106 ż¼ąĪżĄżżż╬żŪĪó╚½╠Į╦„ż¼żŪżŁżļĪŻ ? Ż©▒ĒŽ“żŁż╬ź│źżź¾ż“żęż├ż»żĻĘĄż╣├Č╩²Ż®+Ż©čYŽ“żŁż╬ź│źżź¾ż“żęż├ż»żĻĘĄ ż╣├Č╩²Ż®= ? żŪżóżļĮMż“╚½═©żĻįćżĘĪó┤ż©ż╬ūŅ┤¾éÄż“Ū¾żßżļĪŻ
- 6. å¢Ņ} B ©C źóźß®`źą
- 7. å¢Ņ}Ė┼ę¬ ? ┐k ? ź▐ź╣Īó║ß ? ź▐ź╣ż╬▒P├µż¼żóżĻĪóĖ„ź▐ź╣ż╦źóźß®`źąż¼║╬Ųźż½ż║ ż─żżżļĪŻż┐ż└żĘĪó▒┌ļHż╦żŽżżż╩żżĪŻ ? Ė„źóźß®`źąż¼ 4 Ųźż╦Ęų┴čżĘĪó╔ŽŽ┬ū¾ėęż╬ź▐ź╣żž 1 Ųźż║ż─ęŲäėżĘż┐ĪŻ ? Į±ż╬▒P├µż¼ėļż©żķżņżļż╬żŪĪ󿎿Ėżßż╬▒P├µż“ 1 ż─Ū¾żßżĶĪŻż┐ż└żĘĪó ĮŌżŽ╔┘ż╩ż»ż╚żŌ 1 ż─┤µį┌ż╣żļĪŻ ? 3 Ī▄ ?, ? Ī▄ 500
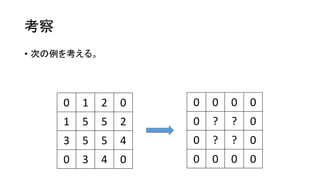
- 8. ┐╝▓ņ ? ┤╬ż╬└²ż“┐╝ż©żļĪŻ 0 1 2 0 1 5 5 2 3 5 5 4 0 3 4 0 0 0 0 0 0 ? ? 0 0 ? ? 0 0 0 0 0
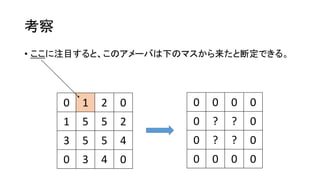
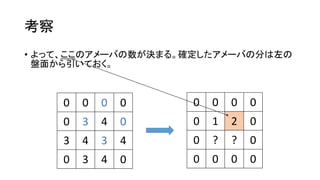
- 9. ┐╝▓ņ ? ż│ż│ż╦ūó─┐ż╣żļż╚Īóż│ż╬źóźß®`źążŽŽ┬ż╬ź▐ź╣ż½żķ└┤ż┐ż╚ČŽČ©żŪżŁżļĪŻ 0 1 2 0 1 5 5 2 3 5 5 4 0 3 4 0 0 0 0 0 0 ? ? 0 0 ? ? 0 0 0 0 0
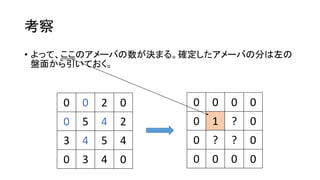
- 10. ┐╝▓ņ ? żĶż├żŲĪóż│ż│ż╬źóźß®`źąż╬╩²ż¼øQż▐żļĪŻ┤_Č©żĘż┐źóźß®`źąż╬ĘųżŽū¾ż╬ ▒P├µż½żķę²żżżŲż¬ż»ĪŻ 0 0 2 0 0 5 4 2 3 4 5 4 0 3 4 0 0 0 0 0 0 1 ? 0 0 ? ? 0 0 0 0 0
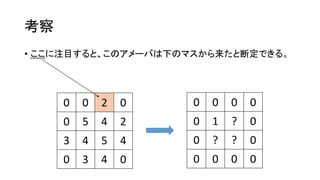
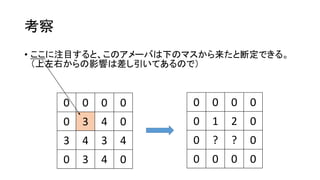
- 11. ┐╝▓ņ ? ż│ż│ż╦ūó─┐ż╣żļż╚Īóż│ż╬źóźß®`źążŽŽ┬ż╬ź▐ź╣ż½żķ└┤ż┐ż╚ČŽČ©żŪżŁżļĪŻ 0 0 2 0 0 5 4 2 3 4 5 4 0 3 4 0 0 0 0 0 0 1 ? 0 0 ? ? 0 0 0 0 0
- 12. ┐╝▓ņ ? żĶż├żŲĪóż│ż│ż╬źóźß®`źąż╬╩²ż¼øQż▐żļĪŻ┤_Č©żĘż┐źóźß®`źąż╬ĘųżŽū¾ż╬ ▒P├µż½żķę²żżżŲż¬ż»ĪŻ 0 0 0 0 0 3 4 0 3 4 3 4 0 3 4 0 0 0 0 0 0 1 2 0 0 ? ? 0 0 0 0 0
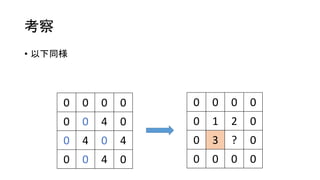
- 13. ┐╝▓ņ ? ż│ż│ż╦ūó─┐ż╣żļż╚Īóż│ż╬źóźß®`źążŽŽ┬ż╬ź▐ź╣ż½żķ└┤ż┐ż╚ČŽČ©żŪżŁżļĪŻ Ż©╔Žū¾ėęż½żķż╬ė░ĒæżŽ▓ŅżĘę²żżżŲżóżļż╬żŪŻ® 0 0 0 0 0 3 4 0 3 4 3 4 0 3 4 0 0 0 0 0 0 1 2 0 0 ? ? 0 0 0 0 0
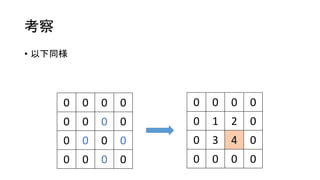
- 14. ┐╝▓ņ ? ęįŽ┬═¼śö 0 0 0 0 0 0 4 0 0 4 0 4 0 0 4 0 0 0 0 0 0 1 2 0 0 3 ? 0 0 0 0 0
- 15. ┐╝▓ņ ? ęįŽ┬═¼śö 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 0 0 3 4 0 0 0 0 0
- 17. å¢Ņ} C ©C ź”źĄź«╠°żė
- 18. å¢Ņ}Ė┼ę¬ ? ? éĆż╬ź▐ź╣ż¼ę╗┴ąż╦üKż¾żŪżżżŲĪóżĮż╬╔Žż╦ ? Ųźż╬ź”źĄź«ż¼żżżļĪŻĖ„ ź”źĄź«żŽū¾ż½ėęż“Ž“żżżŲżżżļĪŻ ? Ė„ź”źĄź«żŽĪóūįĘųż╬─┐ż╬Ū░ż¼┐šżŁź▐ź╣ż╩żķżąĪóźĖźŃź¾źūżĘżŲżĮż╬ź▐ ź╣żžęŲäėżŪżŁżļĪŻ ? ź”źĄź«ż¼źĖźŃź¾źūż╣żļĒśĘ¼ż“øQżßżķżņżļż╚żŁĪóźĖźŃź¾źūż╬Št╗ž╩²ż╬ūŅ ┤¾éÄż“Ū¾żßżĶĪŻ ? 1 Ī▄ ? Ī▄ 105Ż¼? Ī▄ ? Ī▄ 109
- 22. ┐╝▓ņ ? żųż─ż½żļ╬╗ų├ż“╚½═©żĻįćżĘĪóźĖźŃź¾źūż╬Št╗ž╩²ż╬ūŅ┤¾éÄż“Ū¾żßżļŻ┐ Ī· ? Ī▄ 109 ż╩ż╬żŪĪóūŅÉÖ 109 ═©żĻįćż╣ż│ż╚ż╦ż╩żĻģŚżĘżżĪŻ
- 23. ┐╝▓ņ ? źĖźŃź¾źūż╬Št╗ž╩²ż“╩²ż©żŲż▀żļĪŻ 3 ╗ž 4 ╗ž 5 ╗ž
- 24. ┐╝▓ņ ? żųż─ż½żļ╬╗ų├ż¼ėęż╦ 1 ź▐ź╣äėż»ż╚ĪóźĖźŃź¾źūż╬Št╗ž╩²ż¼ 1 ēłż©żļĪŻ ? ū¾é╚ż╬ 2 Ųźż╬źĖźŃź¾źū╗ž╩²ż¼ 1 ż║ż─ēłż©Īóėęé╚ż╬ 1 Ųźż╬źĖźŃź¾źū ╗ž╩²ż¼ 1 £pżļż┐żßĪŻ ? ż│ż╬└²żŪżŽĪóżŪżŁżļż└ż▒ėęż╦╝─ż╗żļż╬ż¼ūŅ▀mĪŻ
- 26. ĮŌĘ© ? ź”źĄź«ż┐ż┴ż“Ū°ķgż╦Ęųż▒żļĪŻ ? Ū°ķgż┤ż╚äeĪ®ż╦ĪóźĖźŃź¾źūż╬Št╗ž╩²ż╬ūŅ┤¾éÄż“ėŗ╦Ńż╣żļĪŻ ? żĮż╬Št║═ż¼┤ż©żŪżóżļĪŻż┐ż└żĘĪ󟬮`źą®`źšźĒ®`ż╦ūóęŌŻĪ ? ėŗ╦Ń┴┐żŽ O(?)
- 27. å¢Ņ} D ©C ▐x▓╩╔½
- 28. å¢Ņ}Ė┼ę¬ ? ? ĒöĄŃ ? ▐xż╬▀BĮYż╩¤oŽ“ź░źķźšż¼ėļż©żķżņżļĪŻ ? ║├żŁż╩ĒöĄŃż½żķ╩╝żßĪó║├żŁż╩ż└ż▒▐xż“▐{ż├żŲżżż»ĪŻ ? ▐{ż├ż┐▐xż╦żŽ │Ó Ī· ŪÓ Ī· │Ó Ī· ŪÓ Ī· ĪŁ ż╬Ēśż╦╔½ż“ēTżļĪŻż┐ż└żĘĪó╔½ żŽ╔ŽĢ°żŁżĄżņżļĪŻ ? ─┐ś╦ż╬▐xż╬┼õ╔½żŽ┐╔─▄ż½┼ąČ©ż╗żĶĪŻ ? 2 Ī▄ ? Ī▄ 2,000Ż¼1 Ī▄ ? Ī▄ 2,000
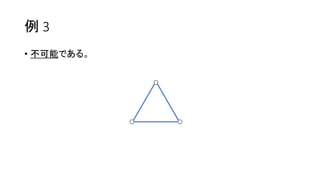
- 33. ┐╝▓ņ ? żĮż│żŪĪó▐xż╬▐{żĻĘĮż“╬┤└┤ż½żķ▀^╚źżžż╚─µŽ“żŁż╦┐╝ż©żŲż▀żļĪŻ ? ż╣żļż╚ĪóĪĖę╗Č╚ēTż├ż┐╔½żŽ╔ŽĢ°żŁżĄżņż╩żżĪ╣ż╚żżż”źļ®`źļż╦ēõż’żļĪŻ Ī· ż│ż╬ĘĮż¼┐╝ż©żõż╣żżŻĪ
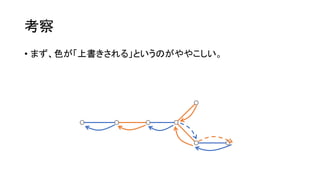
- 34. ┐╝▓ņ ? ╬┤└┤ż½żķ▀^╚źżžż╚┐╝ż©ų▒ż╣ż│ż╚ż╦żĶż├żŲĪó┤╬ż╬żĶż”ż╦å¢Ņ}ż“čįżżōQż© żķżņżļĪŻ ? ╩╝ĄŃż╚żŽżĖżßż╬╔½Ż©│Ó or ŪÓŻ®ż“║├żŁż╦▀xżėĪó║├żŁż╩ż└ż▒▐xż“▐{ż├żŲżżż»ĪŻ ? ▐{ż├ż┐▐xż╦żŽ│ÓŪÓĮ╗╗źż╦╔½ż“ēTżļĪŻż┐ż└żĘĪó╔½żŽ╔ŽĢ°żŁżĄżņż╩żżĪŻ ? ─┐ś╦ż╬▐xż╬┼õ╔½żŽ┐╔─▄ż½┼ąČ©ż╗żĶĪŻ ? ęŖ═©żĘż¼┴╝ż»ż╩ż├ż┐ŻĪ
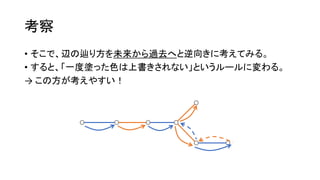
- 35. ┐╝▓ņ ? ?, ? Ī▄ 2,000 ż╚ąĪżĄżżż╬żŪĪó╩╝ĄŃż╚żŽżĖżßż╬╔½żŽ╚½╠Į╦„żŪżŁżĮż”ĪŻ ? └²ż©żąĪóż│ż│ż“╩╝ĄŃż╦ĪóŪÓż½żķ╩╝żßżŲż▀żļĪŻ
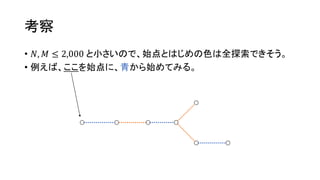
- 40. ŽļČ©š`ĮŌĘ© ? ╩╝ĄŃż╚żŽżĖżßż╬╔½ż“╚½╠Į╦„ż╣żļĪŻ ? ╔ŅżĄā׎╚╠Į╦„żõĘ∙ā׎╚╠Į╦„żŪžØė¹ż╦▐xż“ēTż├żŲżżż»ĪŻ ? ż╣ż┘żŲż╬▐xż“ēTżņż┐żķĪóż╣ż░ Ī░YesĪ▒ ż╚┼ąČ©ż╣żļĪŻ ? żĮż”żŪż╩ż▒żņżą Ī░NoĪ▒ ż╚┼ąČ©ż╣żļĪŻ Ī· ųžę¬ż╩ź▌źżź¾ź╚ż“ęŖ┬õż╚żĘżŲżżżļŻĪ
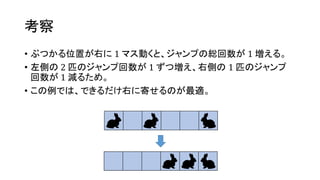
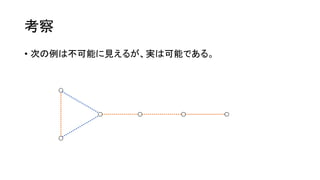
- 44. ┐╝▓ņ ? ę╗ęŖįæż▐ż├ż┐żĶż”ż╦ęŖż©żļż¼Īó╚²ĮŪą╬ż╬ķ]┬Ęż“╗žżļż│ż╚żŪ│Ó / ŪÓż“ Ę┤▄׿ŪżŁżļĪŻ
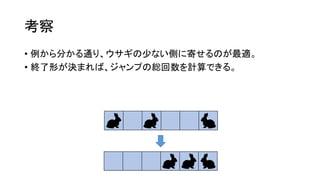
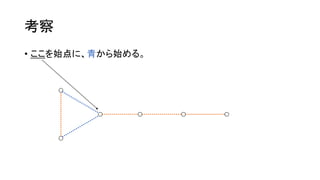
- 46. ┐╝▓ņ ? Ųµ╩²ķLż╬ķ]┬Ęż“╗žżļż┤ż╚ż╦│Ó / ŪÓż“Ę┤▄׿ŪżŁżļĪŻ ? żĶż├żŲĪóŲµ╩²ķLż╬ķ]┬Ęż¼═Ļ│╔ż╣żņżąĪóżóż╚żŽż╔ż¾ż╩ēTżĻĘĮżŌ┐╔─▄ŻĪ
- 47. ĮŌĘ© ? ╩╝ĄŃż╚żŽżĖżßż╬╔½ż“╚½╠Į╦„ż╣żļĪŻ ? ╔ŅżĄā׎╚╠Į╦„żõĘ∙ā׎╚╠Į╦„żŪžØė¹ż╦▐xż“ēTż├żŲżżż»ĪŻ ? ż╣ż┘żŲż╬▐xż“ēTżņż┐żķĪóż╣ż░ Ī░YesĪ▒ ż╚┼ąČ©ż╣żļĪŻ ? Ųµ╩²ķLż╬ķ]┬Ęż¼═Ļ│╔żĘż┐żķĪóż╣ż░ Ī░YesĪ▒ ż╚┼ąČ©ż╣żļĪŻ ? żĮż”żŪż╩ż▒żņżą Ī░NoĪ▒ ż╚┼ąČ©ż╣żļĪŻ ? ėŗ╦Ń┴┐żŽ O(??)
















![┐╝▓ņ
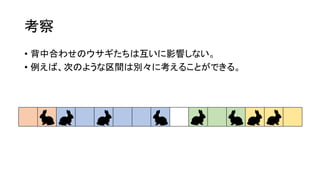
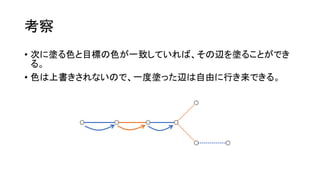
? ╔ŅżĄā׎╚╠Į╦„żõĘ∙ā׎╚╠Į╦„żŪ┤╬ż╬żĶż”ż╦ēTżņżļĪŻ
? ╚²ĮŪą╬ż╬ķ]┬Ęż¼żŪżŁż┐ż╬ż¼ź▌źżź¾ź╚ĪŻ](https://image.slidesharecdn.com/arc041-150704133030-lva1-app6891/85/Arc041-43-320.jpg)
![┐╝▓ņ
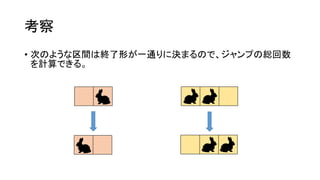
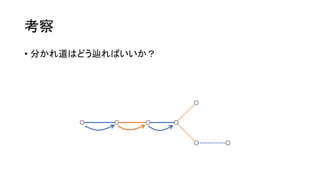
? ę╗ęŖįæż▐ż├ż┐żĶż”ż╦ęŖż©żļż¼Īó╚²ĮŪą╬ż╬ķ]┬Ęż“╗žżļż│ż╚żŪ│Ó / ŪÓż“
Ę┤▄׿ŪżŁżļĪŻ](https://image.slidesharecdn.com/arc041-150704133030-lva1-app6891/85/Arc041-44-320.jpg)
![┐╝▓ņ
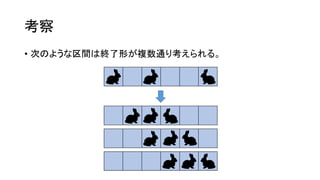
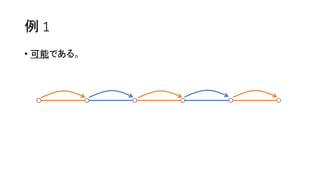
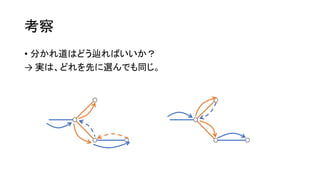
? į┘żė╚²ĮŪą╬ż╬ķ]┬Ęż“╗žżĻĪóż╣ż┘żŲż╬▐xż“ēTżņż┐ĪŻ](https://image.slidesharecdn.com/arc041-150704133030-lva1-app6891/85/Arc041-45-320.jpg)
![┐╝▓ņ
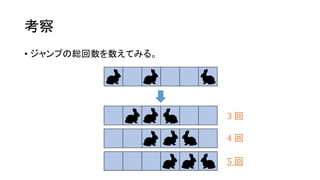
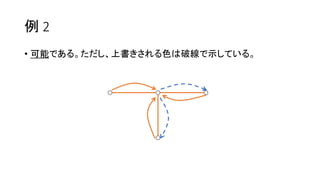
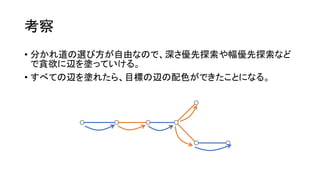
? Ųµ╩²ķLż╬ķ]┬Ęż“╗žżļż┤ż╚ż╦│Ó / ŪÓż“Ę┤▄׿ŪżŁżļĪŻ
? żĶż├żŲĪóŲµ╩²ķLż╬ķ]┬Ęż¼═Ļ│╔ż╣żņżąĪóżóż╚żŽż╔ż¾ż╩ēTżĻĘĮżŌ┐╔─▄ŻĪ](https://image.slidesharecdn.com/arc041-150704133030-lva1-app6891/85/Arc041-46-320.jpg)
![ĮŌĘ©
? ╩╝ĄŃż╚żŽżĖżßż╬╔½ż“╚½╠Į╦„ż╣żļĪŻ
? ╔ŅżĄā׎╚╠Į╦„żõĘ∙ā׎╚╠Į╦„żŪžØė¹ż╦▐xż“ēTż├żŲżżż»ĪŻ
? ż╣ż┘żŲż╬▐xż“ēTżņż┐żķĪóż╣ż░ Ī░YesĪ▒ ż╚┼ąČ©ż╣żļĪŻ
? Ųµ╩²ķLż╬ķ]┬Ęż¼═Ļ│╔żĘż┐żķĪóż╣ż░ Ī░YesĪ▒ ż╚┼ąČ©ż╣żļĪŻ
? żĮż”żŪż╩ż▒żņżą Ī░NoĪ▒ ż╚┼ąČ©ż╣żļĪŻ
? ėŗ╦Ń┴┐żŽ O(??)](https://image.slidesharecdn.com/arc041-150704133030-lva1-app6891/85/Arc041-47-320.jpg)































































