Pythagoras i h├żftet
- 1. Nu handlar det om r├żtvinkliga trianglar och Pythagoras sats. Inger B├żckstr├Čm, Burtr├żsk 1
- 2. Sl├ź upp en ren sida i ditt r├żkneh├żfte. Inger B├żckstr├Čm, Burtr├żsk 2
- 3. Du ska rita en geometrisk figur p├ź denna sida. Titta och lyssna s├ź f├źr du veta vad och hur du ska g├Čra det. Inger B├żckstr├Čm, Burtr├żsk 3
- 4. N├żr du ritar ska du anv├żnda linjal och du ska f├Člja linjerna och rutorna som finns p├ź sidan i ditt r├żkneh├żfte. Inger B├żckstr├Čm, Burtr├żsk 4
- 5. N├żr du ritar en linje ska du b├Črja d├żr tv├ź linjer p├ź sidan i r├żkneh├żftet korsar varandra, allts├ź i ett h├Črn av en ruta p├ź sidan i h├żftet. Samma sak n├żr du avslutar linjen som du ritar; den ska sluta precis d├żr tv├ź linjer i r├żkneh├żftet korsar varandra. Inger B├żckstr├Čm, Burtr├żsk 5
- 6. Tag pennan i din ena hand och linjalen i din andra hand. L├żgg linjalen ungef├żr mitt p├ź sidan. Du ska rita en linje som ├żr 8 cm l├źng. F├Člj linjerna och rutorna i boken EXAKT! G├ź efter d├żr rutorna b├Črjar och slutar om det inte blir exakt 8 cm med linjalen. Rita nu. Inger B├żckstr├Čm, Burtr├żsk 6
- 7. Nu ska du rita en annan linje, vinkelr├żtt mot ena ├żnden av din 8 centimeters linje. Du f├źr v├żlja om du b├Črjar den nya linjen vid b├Črjan eller vid slutet av din f├Črsta linje. B├Črja EXAKT d├żr den f├Črsta linjen b├Črjar eller slutar. Anv├żnd givetvis linjal! G├Čr den nya linjen 6 cm l├źng. EXAKT! F├Člj rutorna. Inger B├żckstr├Čm, Burtr├żsk 7
- 8. Markera den r├żta vinkeln som finns mellan de b├źda linjerna. Markera med symbolen f├Čr ŌĆØr├żt vinkelŌĆØ, ja, du vet hur den ser ut. Eller hur? Inger B├żckstr├Čm, Burtr├żsk 8
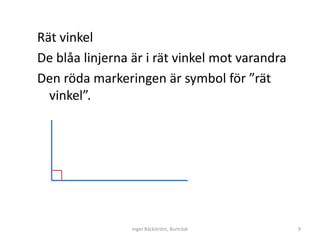
- 9. R├żt vinkel De bl├źa linjerna ├żr i r├żt vinkel mot varandra Den r├Čda markeringen ├żr symbol f├Čr ŌĆØr├żt vinkelŌĆØ. Inger B├żckstr├Čm, Burtr├żsk 9
- 10. Nu ska du g├Čra den r├żta vinkeln till en triangel; en r├żtvinklig triangel. L├żgg linjalen EXAKT d├żr dina tv├ź linjer slutar och dra en tredje linje som binder samman de b├źda ├żndpunkterna. Nu har du ritat en r├żtvinklig triangel. Och gjort det noggrant! Inger B├żckstr├Čm, Burtr├żsk 10
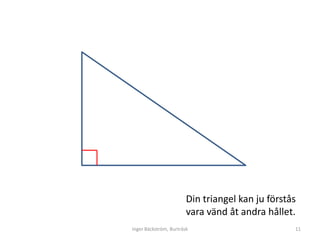
- 11. Din triangel kan ju f├Črst├źs vara v├żnd ├źt andra h├źllet. Inger B├żckstr├Čm, Burtr├żsk 11
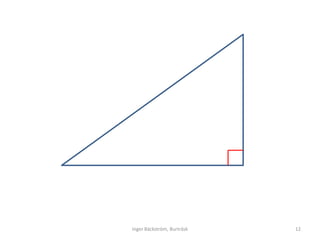
- 12. Inger B├żckstr├Čm, Burtr├żsk 12
- 13. M├żt den tredje sidan i din triangel. Hur l├źng ├żr den? Skriv inte upp det, ├żn. Inger B├żckstr├Čm, Burtr├żsk 13
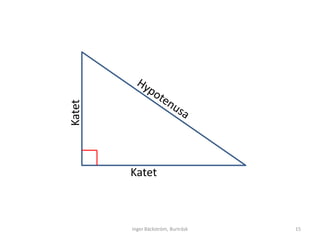
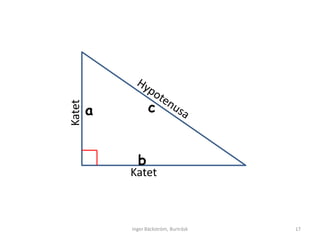
- 14. Vad kallas sidorna i en r├żtvinklig triangel? Skriv namnet l├żngs med r├żtt sida i din triangel. V├żlj ur dessa tre: Katet Katet Hypotenusa Inger B├żckstr├Čm, Burtr├żsk 14
- 15. Katet Katet Inger B├żckstr├Čm, Burtr├żsk 15
- 16. Nu ska du namnge sidorna i triangeln med hj├żlp av en bokstav. Skriv p├ź insidan av sidorna, inuti triangeln, och det ska vara sm├ź bokst├żver: Vid den kortaste kateten: a Vid den l├żngsta kateten: b Vid hypotenusan: c (den l├żngsta sidan i triangeln) Inger B├żckstr├Čm, Burtr├żsk 16
- 17. a c Katet b Katet Inger B├żckstr├Čm, Burtr├żsk 17
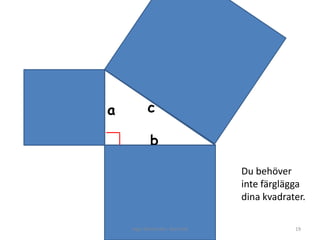
- 18. Den gamla greken Pythagoras gjorde kvadrater p├ź alla tre sidor av en r├żtvinklig triangel. Kvadraternas sidor var lika l├źnga som l├żngden p├ź kateterna och hypotenusan. Rita kvadrater du ocks├ź. G├Čr de s├ź hela som du kan, som ryms p├ź sidan. Inger B├żckstr├Čm, Burtr├żsk 18
- 19. a c b Du beh├Čver inte f├żrgl├żgga dina kvadrater. Inger B├żckstr├Čm, Burtr├żsk 19
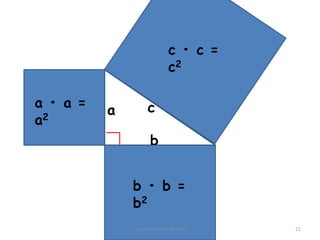
- 20. Han kunde r├żkna ut arean p├ź de tre kvadraterna s├ź h├żr: a ŌĆó a eller som man ocks├ź kan skriva det a2 b ŌĆó b eller b2 c ŌĆó det i dina kvadrater. Skriv c eller c2 Inger B├żckstr├Čm, Burtr├żsk 20
- 21. c ŌĆó c = c2 a ŌĆó a = c a a2 b b ŌĆó b = b2 Inger B├żckstr├Čm, Burtr├żsk 21
- 22. Sedan kom han p├ź n├źgot bra; han s├źg att det fanns ett samband mellan areorna p├ź kateterna och arean p├ź hypotenusan. Om man l├żgger ihop areorna p├ź kateterna s├ź blir deras area tillsammans lika stor som arean p├ź hypotenusan. Och det g├żller i alla r├żtvinkliga trianglar. Inger B├żckstr├Čm, Burtr├żsk 22
- 23. Skriv detta i ditt r├żkneh├żfte, nedanf├Čr din triangel: Pythagoras sats a 2 + b 2 = c2 Inger B├żckstr├Čm, Burtr├żsk 23
- 24. Pythagoras sats anv├żnds till ŌĆó att r├żkna ut l├żngden p├ź n├źgon av sidorna i en r├żtvinklig triangel ŌĆó att kontrollera om en triangel har en r├żt vinkel Inger B├żckstr├Čm, Burtr├żsk 24
- 25. Ber├żkna hypotenusans l├żngd i den triangel du har ritat. Skriv i ditt r├żkneh├żfte: a2 + b2 = c2 a = 6 cm b = 8 cm c = ? 6 ŌĆó 6 + 8 ŌĆó 8 = c2 36 + 64 = c2 100 = c2 c2 = 100 c= ŌłÜ100 c = 10 Svar: Hypotenusan ├żr 10 cm l├źng Inger B├żckstr├Čm, Burtr├żsk 25
- 26. ├är triangeln r├żtvinklig? Triangeln ├żr r├żtvinklig om Pythagoras sats st├żmmer. Vi kollar det. a2 + b2 = c2 I en likhet, ekvation, ska det som st├źr p├ź var sin sida om likhetstecknet vara lika f├Čr att likheten ska g├żlla. Man brukar s├żga att V├żnster led ska vara lika med H├Čger led V.L. = H.L. Inger B├żckstr├Čm, Burtr├żsk 26
- 27. V.L. = a2 + b2 H.L. = c2 V.L. = 6 ŌłÖ 6 + 8 ŌłÖ 8 H.L. = 10 ŌłÖ 10 V.L. = 36 + 64 H.L. = 100 V.L. = 100 H.L.= 100 V.L. = H.L. Triangeln har en r├żt vinkel. Svar: Det ├żr en r├żtvinklig triangel. Inger B├żckstr├Čm, Burtr├żsk 27
- 28. Om det ├żr s├ź att hypotenusan ├żr 9 cm ist├żllet. Vi kollar om vi har en r├żtvinklig triangel. a2 + b2 = c2 V.L. = a2 + b2 H.L. = c2 V.L. = 6 ŌłÖ 6 + 8 ŌłÖ 8 H.L. = 9 ŌłÖ 9 V.L. = 36 + 64 H.L. = 81 V.L. = 100 H.L.= 81 V.L. ŌēĀ H.L. (ŌēĀ betyder ŌĆØinte lika medŌĆØ) Triangeln har ingen r├żt vinkel. Svar: Triangeln ├żr inte r├żtvinklig. Inger B├żckstr├Čm, Burtr├żsk 28
- 29. I en r├żtvinklig triangel ├żr hypotenusan 13 cm och den l├źnga kateten 12 cm. Ber├żkna den korta katetens l├żngd. a c (Rita alltid en figur, triangel, och s├żtt ut a, b och c). b a2 + b2 = c2 a2 =? b = 12 cm c = 13 cm F├Čr att r├żkna ut l├żngden p├ź a vill vi ha a2 ensam p├ź ena sidan om likhetstecknet. T├żnk p├ź hur du har l├żrt dig att l├Čsa ekvationer, g├Čra lika p├ź b├źda sidor om likhetstecknet. Inger B├żckstr├Čm, Burtr├żsk 29
- 30. Vi tar bort b2 fr├źn b├źda sidor om likhetstecknet: a2 + b2 - b2 = c2 - b2 och f├źr kvar: a2 = c2 - b2 Nu s├żtter vi in de v├żrden vi har och g├Čr ber├żkningar: a2 = 13 ŌłÖ 13 - 12 ŌłÖ 12 a2 = 169- 144 a2 = 25 a =ŌłÜ25 a =5 Svar: Kateten ├żr 5 cm l├źng Inger B├żckstr├Čm, Burtr├żsk 30